中考数学冲刺复习相似三角形存在性问题一

中考数学冲刺复习相似三角形存在性问题一

中考数学冲刺复习

相似三角形

存在性问题一

【前言】相似三角形问题是近来二次函数综合题中出现最多的问题之一，题型变化多样，方法多样，使其难度又增加了几分，本专题分三节内容，注意介绍关于相似三角形存在性问题在中考中的考点及解法分析。

【问题与方法】

（1)从相似的判定说起常用的相似三角形判定方法有：

    判定1:三边对应成比例的两个三角形是相似三角形；

    判定2:两边对应成比例且夹角相等的两个三角形是相似三角形；

    判定3:有两组角对应相等的三角形是相似三角形．

    在解决问题时，判定2、3应用更多，且这两个判定均有相等角条件，所以可考虑从角着手。

【思路概括】

    关键：先确定一组相等角。    

    然后再找：

    思路1:两相等角的两边对应成比例；

    思路2:还存在另一组角相等．

    事实上，在坐标系中，已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1.

（2)题型分析

    通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点．即可分为“单动点”类、“双动点”两类问题。

本讲讨论关于“单动点类问题”

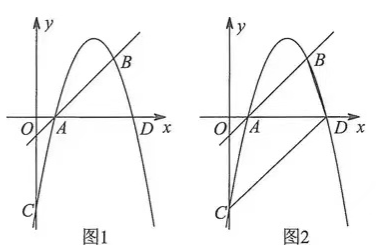
例1:如图1,在平面直角坐标系中，直线y=x-1与抛物线y=-x²+bx+c交于A、B两点，其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.

（1)求m、n的值及该抛物线的解析式；

（2)如图2,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与ΔABD相似，若存在，请直接写出点Q的坐标；若不存在，请说明理由。    

【解析】

（1)m=1,n=3,抛物线解析式为y=-x²+6x-5;

（2)

【思路】：平行得相等角，构造两边成比例

    由题意得D(5, 0),

    ∴直线CD解析式为：y=x-5,

    ∴ CD//AB,

    ∴ ∠CDA=∠BAD,

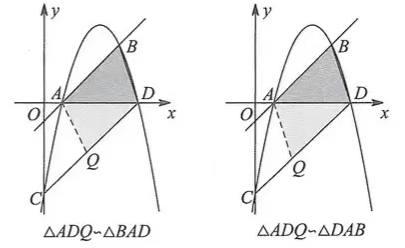
    ①当ΔADQ～ΔBAD时，

      DA/AB=DQ/AD，代入解得：DQ=8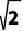/3

      得点Q坐标为（7/3，-8/3),    

数学陈老师:

    ②当ΔADQ～ΔDAB时

      DA/DQ=AD/AB,代入解得：DQ=3,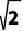

      得点Q坐标为（2,-3).

     综上，Q点坐标为（7/3,-8/3)或（2,-3).

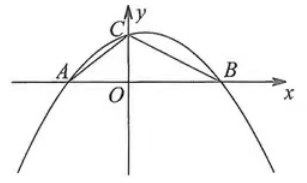
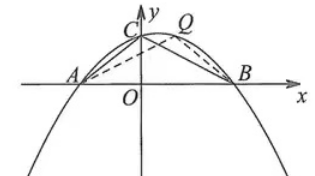
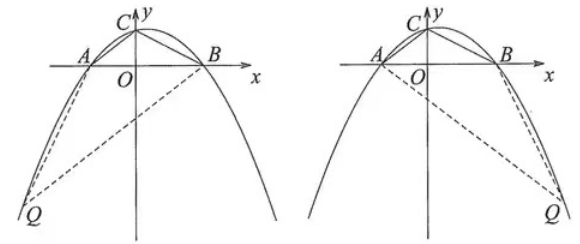
例2:如图，在直角坐标系中，直线y=-1/2x+3与x轴、y轴分别交于点B、点C,对称轴为x=1的抛物线过B、C两点，且交x轴于另一点A,连接AC.

（1)直接写出点A、点B、点C的坐标和抛物线的解析式；

（2)抛物线上是否存在一点Q(点C除外），使以点Q、A、B为顶点的三角形与ΔABC相似？若存在，求出点Q的坐标；若不存在，请说明理由。

【解析】    

（1)A(-4, 0)、B(6, 0)、C(0, 3),

    抛物线：y=-1/8x²+1/4x+3

（2)当点Q在抛物线上运动时，则对于ΔABQ而言，无一定角，这是本题最大的难点。

    ①当点Q在x轴上方时，根据对称性易得：

      当点Q与点C关于对称轴x=1对称时，

      ΔABQ与ΔABC相似，

      此时Q点坐标为（2, 3);

数学陈老师:

    ②当点Q在x轴下方时，

      不妨先考虑∠ABQ,

    情况1:若∠ABQ=∠ABC,则K_BQ=1/2

           直线BQ解析式：y=1/2x-3,

           联立方程：1/2x-3=-1/8x²+1/4x+3

           解得：x₁=-8,x₂=6(舍），

           ∴Q点坐标为（－8,-7),    

           此时BC=3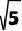,BA=10,BQ=7,

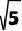    根据线段长度可知∠ABQ与∠ABC的两边并不成比例，

    故（－8,-7)舍掉．

    情况2:若∠ABQ=∠BAC,

           过点B作AC平行线，与抛物线交点即为Q点。

           可得直线BQ解析式：y=3/4x-9/2

           联立方程：3/4x-9/2=-1/8x²+1/4x+3

           解得：x₁=-10,x₂=6(舍），

          ∴Q点坐标为（－10,-12),

           此时AC=5,BA=10,BQ=20,

           即有BA/BA=AB/BQ,

          ∴ ΔCAB～ΔABQ.

    情况3:若∠BAQ=∠ABC,

           根据对称性结合情况1的答案，

           可知此时Q点坐标为（10,-7),且需舍掉；

    情况4:若∠BAQ=∠BAC,

           根据对称性结合情况2的答案，

           可知此时Q点坐标为（12,-12),

           且此时ΔABQ与ΔABC相似。

综上所述，Q点坐标为（2, 3)或（－10,-12)或（12, -12) .

数学陈老师:

【真题演练】

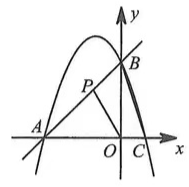
1.如图，在平面直角坐标系xOy中，直线y=kx+3分别交x轴、y轴于A、B两点，经过A、E两点的抛物线y=-x²+bx+c与x轴的正半轴相交于点C (1, 0) .

（1)求抛物线的解析式；

（2)若P为线段AB上一点，∠APO=∠ACB,求AP的长．    

数学陈老师:

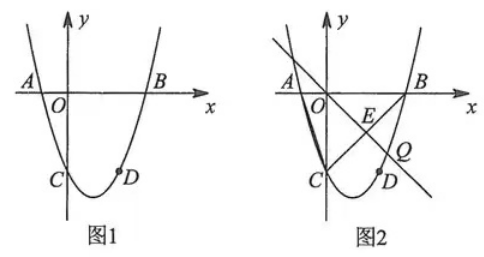
2.如图，抛物线y=ax²+bx+c与x轴交于点A(-1, 0),点B(3, 0),与y轴交于点C,且过点D(2,-3).点Q是抛物线y=ax²+bx+c上的动点．

（1)求抛物线的解析式；

（2)如图2,直线OQ与线段BC相交于点E,当ΔOBE与ΔABC相似时，求点Q的坐标。

数学陈老师:

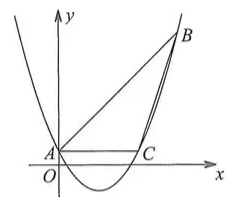
3.如图，已知抛物线y=ax²-2x+c经过ΔABC的三个顶点，其中点A(0, 1),点B(9, 10),AC∥x轴。

（1)求这条抛物线的解析式；

（2)求tan∠ABC的值；

（3)若点D为抛物线的顶点，点E是直线AC上一点，当ΔCDE与ΔABC相似时，求点E的坐标。

数学陈老师:

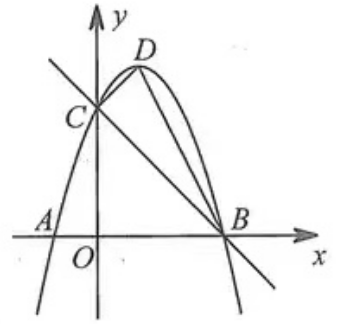
4.如图，以D为顶点的抛物线y=-x²+bx+c交x轴于A、B两点，交y轴于点C,直线BC的表达式为y=-x+3.

（1)求抛物线的表达式；

（2)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与ΔBCD相似？若存在，请求出点Q的坐标；若不存在，请说明理由。    

数学陈老师:

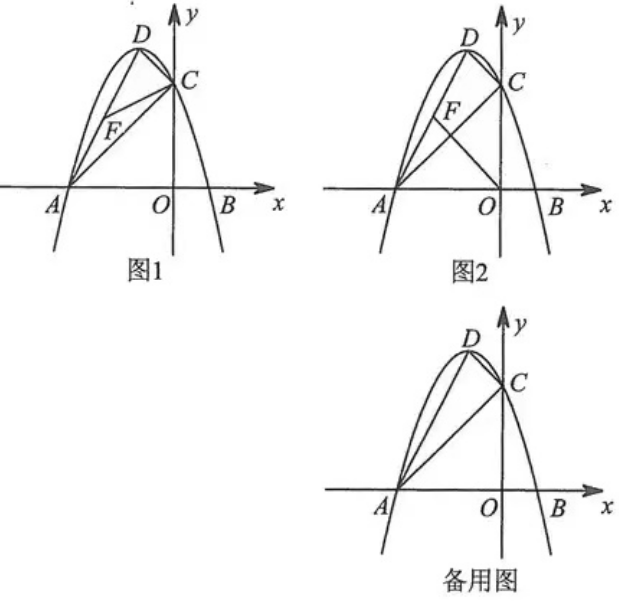
5.已知抛物线y=ax²+bx+3与x轴分别交于A(-3, 0),B(1, 0)两点，与y轴交于点C.

（1)求抛物线的表达式及顶点D的坐标；

（2)点F是线段AD上一个动点．

    ①如图1,设k=AF/AD，当k为何值时，CF=1/2AD?

    ②如图2,以A、F、O为顶点的三角形是否与ΔABC相似？若相似，求出点F的坐标；若不相似，请说明理由。    

【答案】

【分析】创作不易

【详解】赞赏后有解析过程

点赞+关注

学习不迷路