中考数学旋转题总丢分?这5大模型让你一眼看出辅助线

旋转模型是中考数学几何题中的核心考点，掌握其解题技巧能让复杂的几何证明变得清晰明了。这类问题的本质是图形绕定点旋转特定角度，通过构造全等或相似三角形，将分散的条件集中起来，让隐藏的几何关系浮出水面。

在初中数学中，旋转模型主要包含五大经典类型。

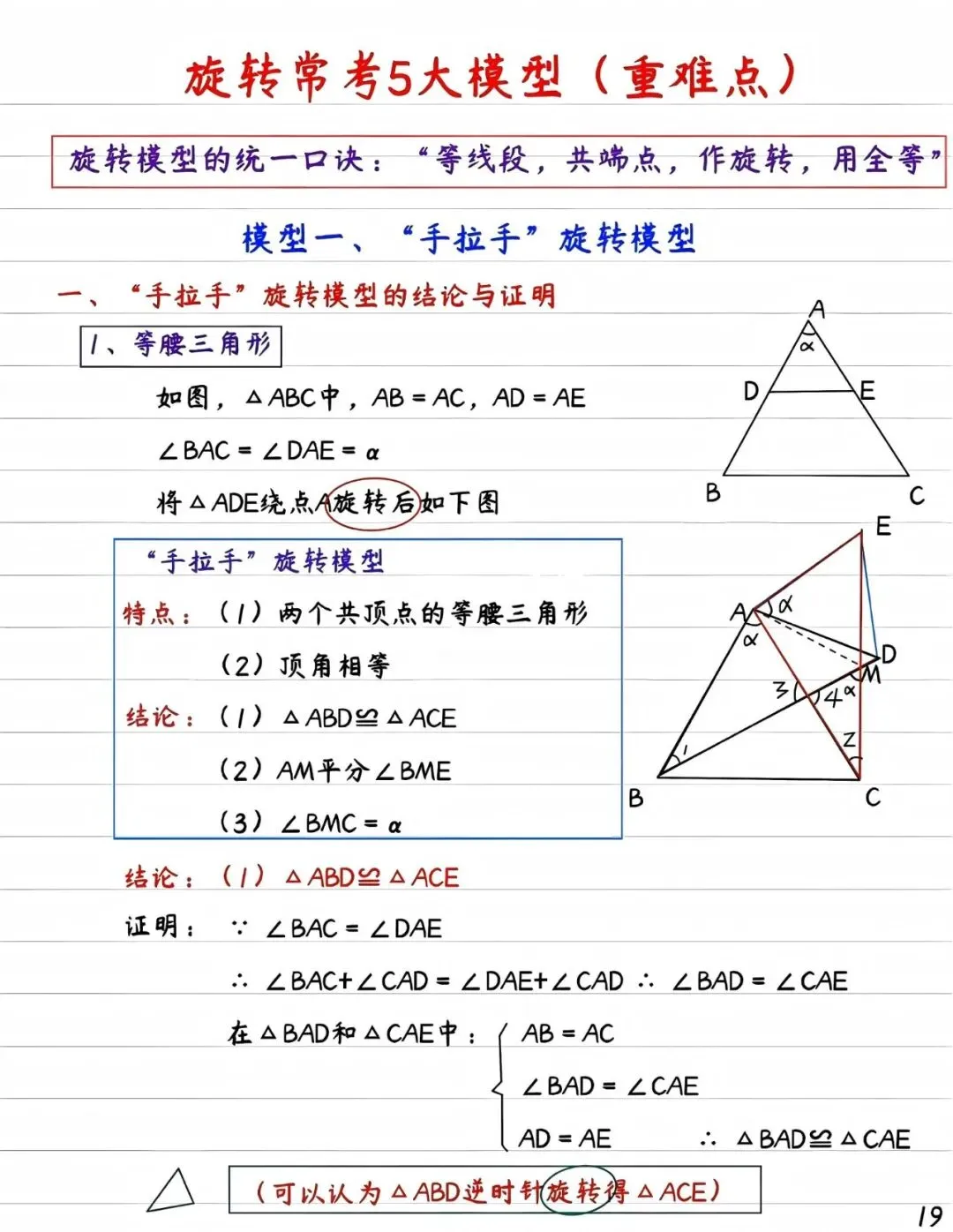
第一种是"手拉手"模型，当两个等腰三角形共享顶点时，旋转会产生全等三角形，对应边夹角恒等于旋转角，这是解决共顶点问题的利器。

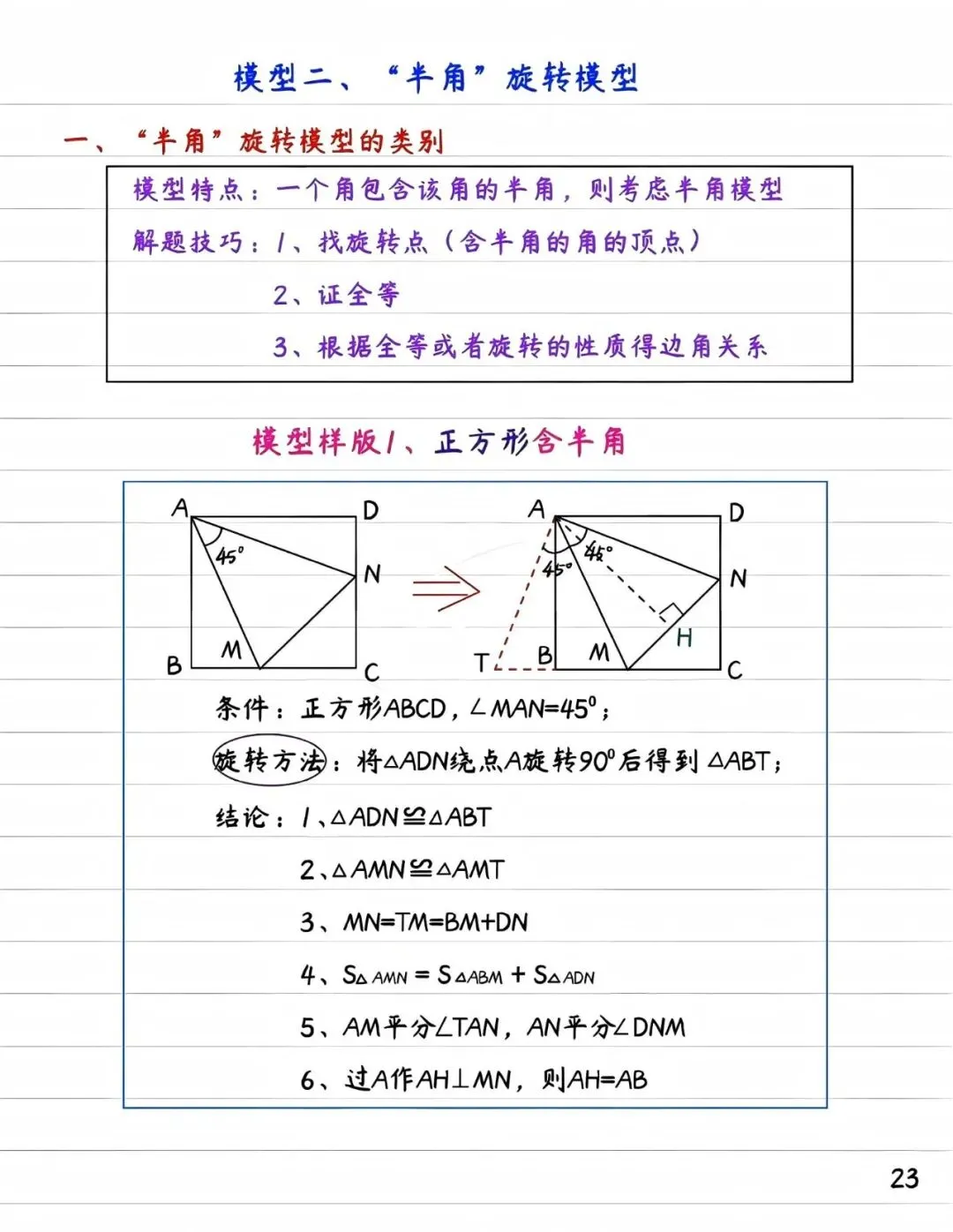
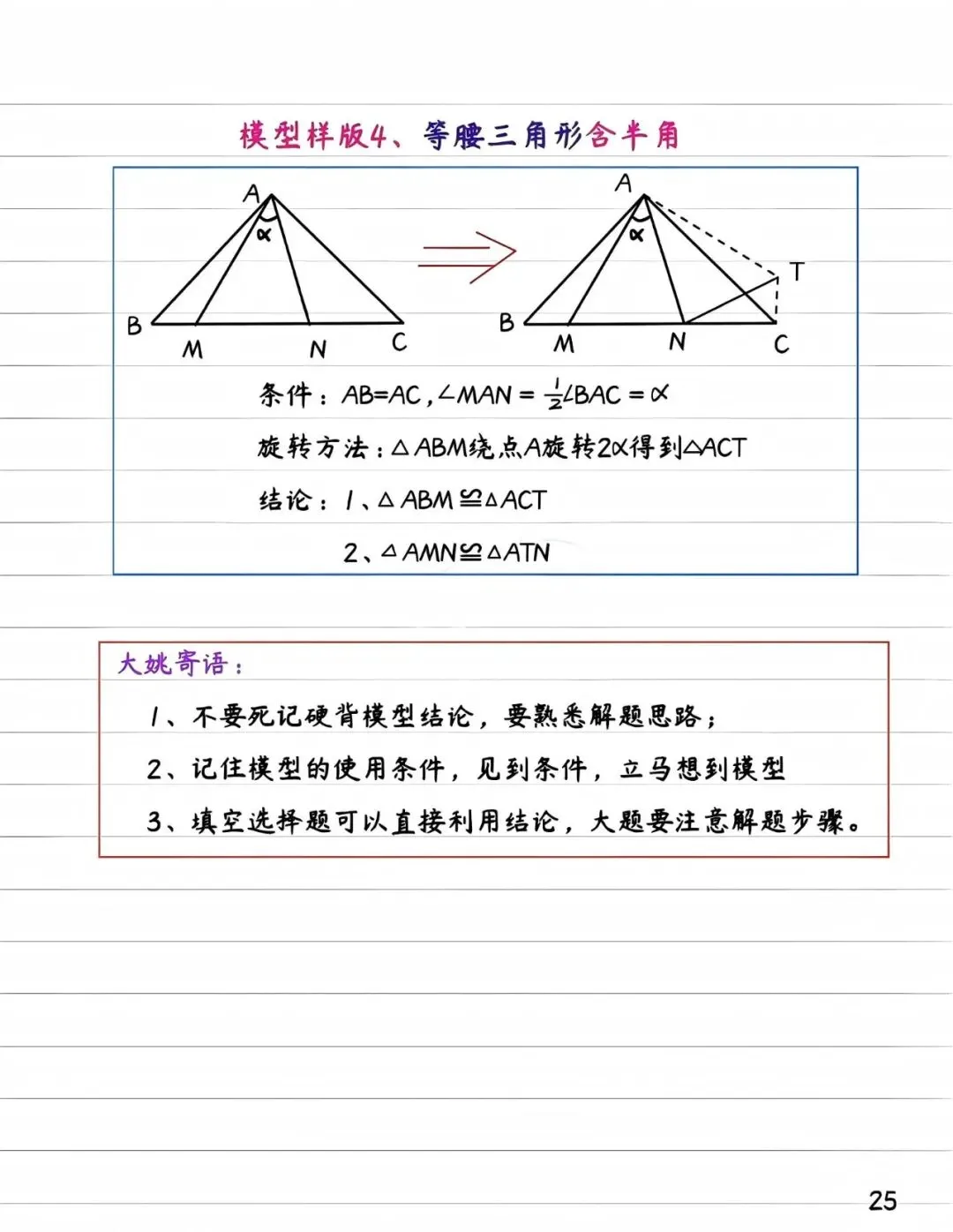
第二种是半角模型，常见于正方形或等腰三角形中，通过将含半角的三角形部分旋转补全，能立即显现边角关系。

第三种是对角互补模型，适用于四边形对角和为180°的情况，旋转其中一三角形会产生对称效果，使对边长度和角度关系一目了然。

第四种是"鸡爪"模型，常出现在等边三角形和等腰直角三角形中，当图形内出现"一点三线"和等边条件时，通过旋转可构造等边三角形和直角三角形。

第五种是费马点问题，通过120°旋转构造等边三角形，最终找到点到三顶点的最短距离和。

面对旋转类题目，同学们需要牢记一个核心口诀："等线段，共端点，作旋转，用全等"。解题时建议先用彩色笔标注旋转前后的对应点，像给几何图形贴上导航标签。当看到"等腰"、"等边"、"正方形"等关键词时，就要想到可能需要运用旋转思想。特别要注意，旋转不是目的，构造全等三角形才是终极目标。

学习旋转模型切忌死记硬背，关键在于熟悉解题思路和使用条件。填空选择题可以直接利用模型结论快速作答，但大题必须写出完整的证明步骤。建议同学们在练习时先画出旋转前后的对比图，让几何关系像电影分镜般清晰呈现，这样才能真正掌握旋转的精髓，在中考中从容应对各类几何难题。