根植基础彰显生长内化素养--一道中考几何压轴题的命制设计与思考

根植基础 彰显生长 内化素养

——一道中考几何压轴题的命题历程与思考

湖北省竹溪县水坪镇中心学校卢均

摘要：教材与基础是命题的源头活水与价值锚点，中考数学命题应注重在矛盾平衡中落实多项素养的综合考察，同时要打破定式，注意启迪思维，彰显探究与生长。

关键词：压轴题；核心素养；通性通法；探究性

一试题呈现

在Rt△ABC中，∠ACB=90°。

(1)如图1，CD⊥AB于D，求证：△ACD∽△ABC。

(2)如图2，CD⊥AB于D，E在CA的延长线上，且CE=CB=6，连接DE,BE。∠ADE=45°，

①求证：AE=AC。

②求△BDE的面积。

(3)如图3，E在CA的延长线上，且CE=CB，连接DE,BE.延长CD交BE于F，

∠ADE=45°，若D是CF的中点，探究BF与EF的数量关系，并说明理由。

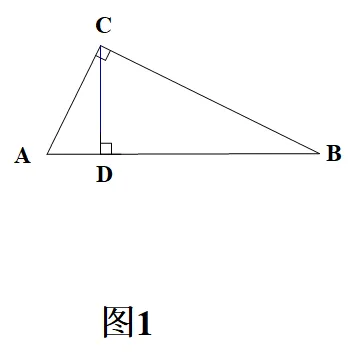
本题源自教材习题的深度改编，以直角三角形为基本框架，通过点的运动与位置变化，层层递进地考查了相似三角形的判定与性质、直角三角形的性质、勾股定理等核心知识，以及几何推理与运算能力。以下从命题依据、原则、设计分析等方面展开论述。

二命题依据

本题严格依据《义务教育数学课程标准（2022年版）》（以下简称“新课标”）进行命制，具体依据体现在以下方面：

1. 内容要求

新课标在“图形与几何”领域对第三学段（7-9年级）提出了明确要求：“理解相似三角形的判定定理及其应用”，“掌握等腰三角形的性质”，“理解直角三角形的性质，掌握勾股定理”^[1]。

本题的三个设问分别对应这些内容要求：

第(1)问直接对应“两角分别相等的两个三角形相似”这一基本判定方法；

第(2)问涉及等腰三角形的性质与直角三角形的综合应用；

第(3)问则需要综合运用相似三角形、等腰三角形和中点性质进行探究

2. 学业要求

新课标在学业要求中明确指出：“能从几何图形的运动变化中发现问题、提出问题，能综合运用几何知识解决问题”。本题通过点E在CA延长线上的位置变化，创设了动态的几何情境，考查学生在图形变化中把握不变关系的能力。

3. 核心素养

新课标强调“以核心素养为导向，关注数学本质，关注通性通法”^[2]。本题以直角三角形中的垂直关系为基本图形，通过层层递进的设问，引导学生运用相似三角形的“基本图形”解决问题，体现了对几何直观和推理能力的考查。

4. 教材依据

本题直接源于人教版教材的经典习题：

第(1)问取材于九年级下册第36页练习第2题（直角三角形中的相似基本图形）。

第(2)(3)问在此基础上进行拓展，延深。

三命题原则

根据新课标理念，本题遵循以下命题原则：

1. 科学性原则

试题表述准确无歧义，图形与文字匹配清晰。三个设问层层递进，逻辑关系严密，几何条件充分且必要，符合数学学科的科学性要求。题目中“CD⊥AB”“CE=CB”“D是CF的中点”等条件清晰明确，图形标注规范，保证了试题的科学严谨。

2. 基础性与发展性相结合的原则

试题既注重考查基础知识（第1问的相似三角形判定），又关注学生的思维发展（第3问的探究性设问）。从“求证”到“求面积”再到“探究数量关系”，思维层次逐级提升，体现了“根植基础、彰显生长”的命题理念。

3. 素养立意原则

试题坚持素养导向，突出对数学核心素养的考查。三个设问分别对应不同的素养要求：第(1)问侧重推理能力的基础训练；第(2)问综合考查几何直观与运算能力；第(3)问则需要较高水平的推理能力和几何直观，体现素养的层级性。

4. 创新性原则

在教材习题的基础上进行创造性改编，通过增加新的条件（如E是CA延长线上一点），改变点的位置（如“D是CF的中点”）、改变设问方式（从证明到探究），使试题具有新颖性和探究价值，体现了“源于教材、高于教材”的命题智慧。

5. 人文性原则

试题图形简洁美观，设问语言亲切自然，从特殊到一般的探究路径符合学生的认知规律，有助于减轻考试焦虑，体现以人为本的理念。

四设计分析

（一）设计意图与多维细目表

设计意图：本题以直角三角形为基本背景，以“垂直→相似→等腰→中点”为主线，通过层层递进的设问，考查学生对相似三角形、等腰三角形性质的综合应用能力，以及在复杂图形中识别基本图形、进行逻辑推理的能力。第(1)问为基础铺垫；第(2)问在具体数值条件下进行计算探究；第(3)问上升为一般性探究，考查学生的数学抽象和推理能力。

（二）考查内容分析

1. 核心知识考查

图形与几何领域：相似三角形的判定与性质、等腰三角形的性质、直角三角形的性质、勾股定理、中点的性质。

数与代数领域：代数运算、方程思想（在面积计算中体现）

2. 关键能力考查

几何直观：从复杂图形中识别基本图形（如“A型”相似、双垂直图形）。

推理能力：从已知条件出发，进行有条理的逻辑推理。

运算能力：在面积计算中进行准确的代数运算。

模型观念：将几何问题转化为数学模型进行求解^[3]。

（三）设计亮点

1. 一图多变，凸显关联

三个小题共用基本图形，但通过点E的位置变化和条件变化，使图形逐步复杂化。这种“一图多用”的设计，有助于学生理解几何图形之间的内在联系，体会“变中不变”的数学思想。

2. 层层递进，螺旋上升

第(1)问直接源于教材，为后续问题提供基础；第(2)问增加具体数值，要求学生进行计算；第(3)问去掉具体数值，改为探究性设问。三个设问形成“基础—应用—探究”的完整链条，符合学生的认知规律。

3. 立足教材，高于教材

试题以教材习题为生长点，通过适当的拓展延伸，使基础题生长为具有较好区分度的压轴题。第(1)问直接引用教材原题，第(2)(3)问则在原题基础上进行创新改编，体现了“源于教材、高于教材”的命题理念。

4. 设问开放，引导探究

第(3)问“探究BF与EF的数量关系”采用开放式设问，要求学生先猜想再证明，考查学生的探究能力和创新意识。这种设问方式符合新课标“增加探究性、开放性试题”的要求。

（四）素材来源

本题素材源于人教版教材两个学段的经典习题：

原始素材1：九年级下册第36页练习第2题：如图1，Rt△ABC中，CD是斜边AB上的高，求证：（1）△ACD∽△ABC；（2）△CBD∽△ABC^[4]。

原始素材2：八年级上册第14页练习第1题：如图，∠ACB=90°，CD⊥AB，垂足为D，∠ACD与∠B有什么关系？为什么？^[5]

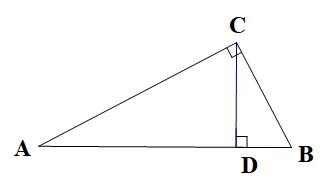
笔者将两个不同年级的素材进行有机融合，通过添加点E在CA延长线上的运动，以及“CE=CB”“D是CF的中点”等条件，使试题既有深厚的教材基础，又有新颖的探究价值。

（五）编制过程

第一步：确定基本框架

以九年级下册第36页练习第2题为基础图形，确定以“直角三角形斜边上的高”为核心的基本图形框架。

第二步：融入等腰元素

受八年级上册第14页等腰三角形性质练习的启发，在CA延长线上取点E，构造等腰三角形（第2问CE=CB，第3问CE=BE），增加问题的综合性和探究性。

第三步：分层设问设计

第(1)问：保留教材原题，作为基础铺垫。

第(2)问：添加BC=CE=6的具体条件，设置中点证明和面积计算两个小问，考查应用能力。

第(3)问：去掉具体数值，增加“D是CF的中点”的条件，设问改为探究线段数量关系，提升思维层次。

第四步：图形与文字打磨

精心绘制三个图形，确保图文匹配、标注清晰。反复推敲文字表述，确保无歧义、无冗余。

第五步：难度预估与调整

根据各小问的思维层次和计算复杂程度，预估难度系数，确保试题有合理的区分度。

（六）命题反思

1. 试题的优点

基础性：第(1)问确保所有学生都能得分，体现学业水平考试的基础性。

层次性：三个设问难度递进，具有良好的区分度。

探究性：第(3)问引导学生经历“猜想—验证—证明”的完整探究过程。

思想性：渗透了数形结合、转化思想、模型思想等数学思想方法。

2. 改进空间

第(2)问的面积计算可以设计多种解法（如直接计算、面积相减等），给学生更多的思维空间。

第(3)问可以进一步追问“请说明你发现的结论”，更明确地引导学生进行探究，可以适当增加实际背景，体现数学的应用价值。

3. 教学启示

本题启示我们在教学中要重视教材习题的教学价值，善于对教材习题进行变式拓展，引导学生从“会做一道题”上升到“会解一类题”。同时要重视基本图形的识别与运用，培养学生的几何直观能力。

（七）命题评价

1. 信度

试题表述清晰，条件充分，图形准确，评分标准客观，保证了测试的信度。第(1)问基础性强，第(2)(3)问区分度好，能够有效测量不同层次学生的学业水平。

2. 效度

试题全面覆盖新课标中“图形与几何”领域的核心内容，有效考查了学生的推理能力、几何直观和模型观念，具有较好的内容效度。

3. 区分度

三个设问难度呈梯度上升，能够较好地区分不同能力水平的学生。预估整体难度系数约为0.65-0.70，符合学业水平考试压轴题的难度要求。

4. 导向性

试题引导教学回归教材、重视基础，同时关注数学思想方法的渗透和核心素养的培养，对初中数学教学具有良好的导向作用。

五 结语

本题以教材经典习题为生长点，通过精心的改编与拓展，形成了一道基础性与生长性并重、知识与能力共融的优质试题。它既考查了学生对核心知识的掌握程度，又关注了数学核心素养的发展水平，体现了新课标理念下学业水平考试命题的方向与追求。

参考文献

[1] 中华人民共和国教育部. 义务教育数学课程标准（2022年版）[S]. 北京: 北京师范大学出版社， 2022. 

[2] 教育部基础教育课程教材专家工作委员会. 义务教育数学课程标准（2022年版）解读[M]. 北京: 北京师范大学出版社， 2022. 

[3] 新课标理念下试题命制的基本原则探索[J]. 中学数学， 2024(04). 

[4] 人民教育出版社课程教材研究所. 义务教育教科书·数学（九年级下册）[M]. 北京: 人民教育出版社， 2013. 

[5] 人民教育出版社课程教材研究所. 义务教育教科书·数学（八年级上册）[M]. 北京: 人民教育出版社， 2013.