第三章 函数(文章最后有电子版资源供大家免费下载)
第一节 3.3 反比例函数 - 考点知识梳理
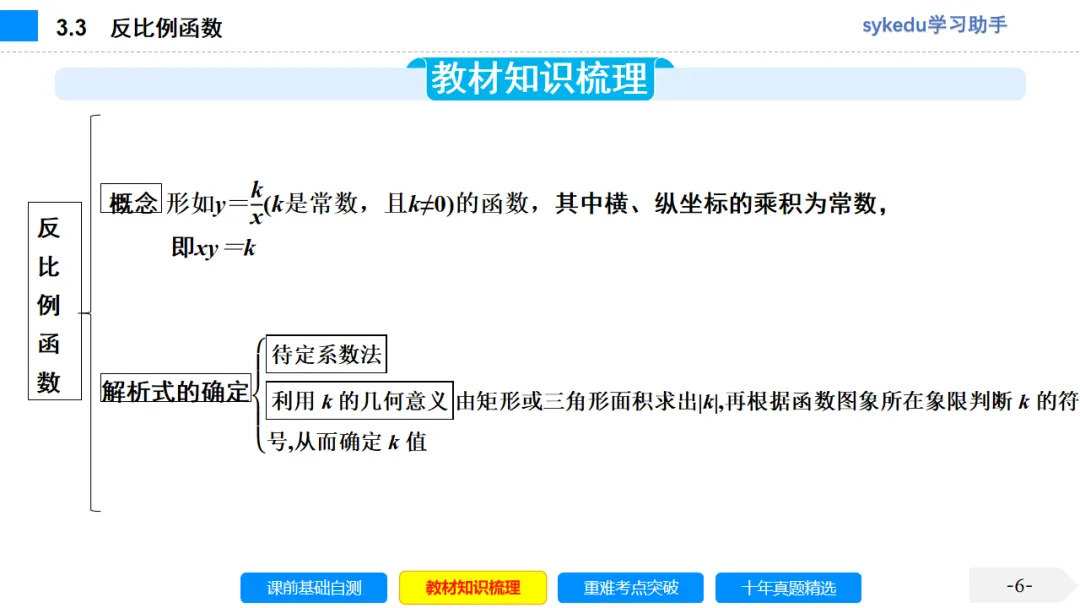
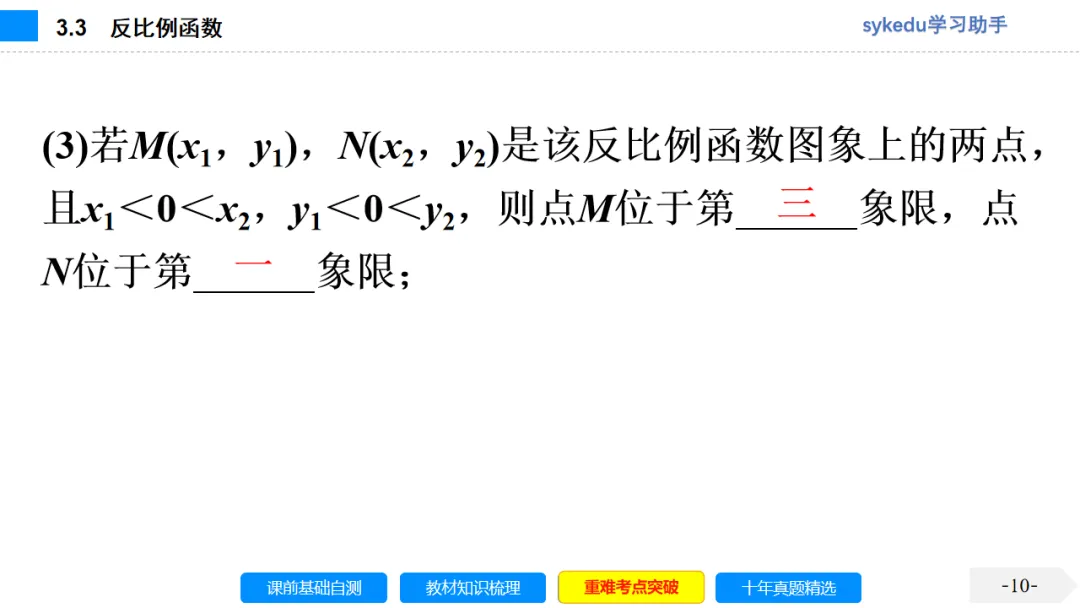
考点一 考点一 反比例函数的定义
一般地,函数y=x(或写成y=kx-1)(k是常数,k≠0)叫做反比例函数.
反比例函数的解析式可以写成xy=k(k≠0),它表明在反比例函数中自变量x与其对应函数值y之积,总等于已知常数k.
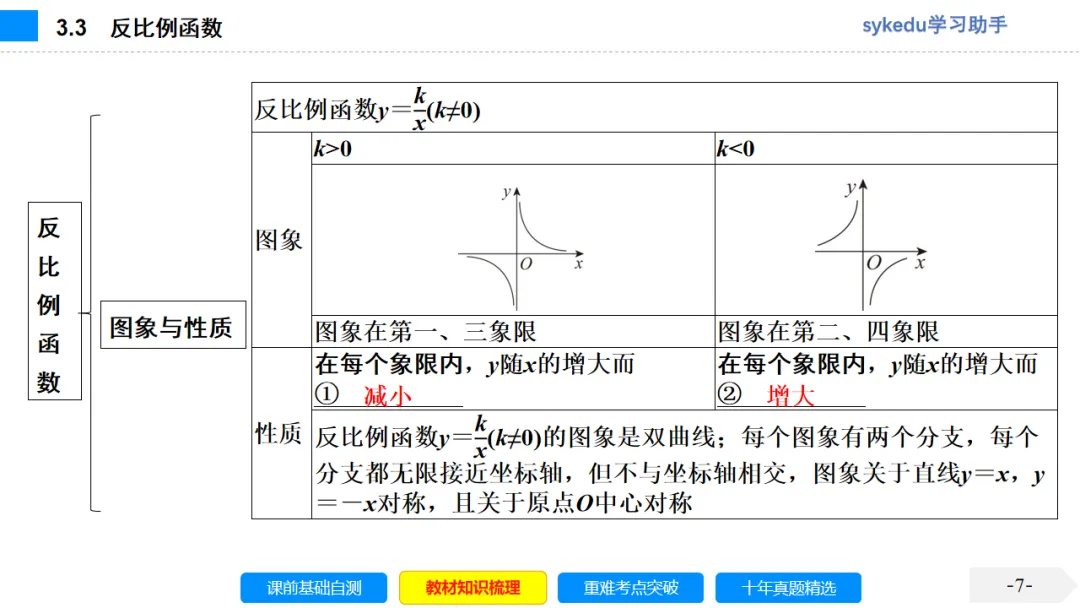
考点二 反比例函数的图象和性质
1.反比例函数y=x(k是常数,k≠0)的图象是双曲线.
因为x≠0,k≠0,相应地y值也不能为0,所以反比例函数的图象无限接近x轴和y轴,但永不与x轴、y轴相交.
2.反比例函数的图象和性质
反比例函数y=x(k是常数,k≠0)的图象总是关于原点对称的,它的位置和性质受k的符号的影响.
y=x(k是常数,k≠0) | k>0 | k<0 |
图 象 |
y=x(k是常数,k≠0) | k>0 | k<0 |
所在象限 | 一、三(x,y同号) | 二、四(x,y异号) |
性 质 | 在每个象限内,y随x的增大而减小 | 在每个象限内,y随x的增大而增大 |
温馨提示
反比例函数的图象是双曲线,它既是轴对称图形,又是中心对称图形.其对称轴是直线y=x和直线y=-x,对称中心是原点.
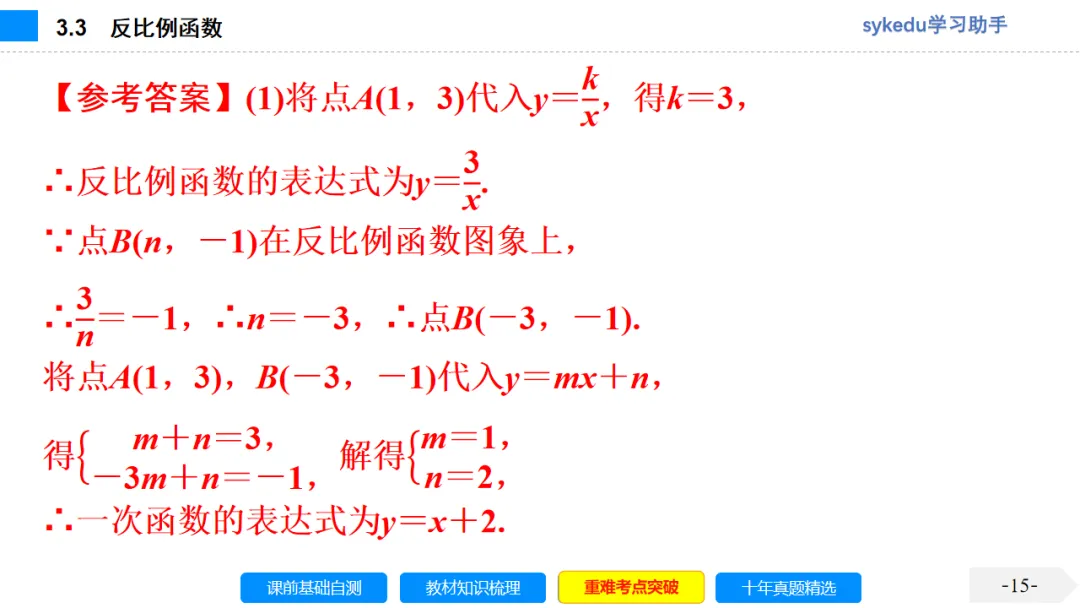
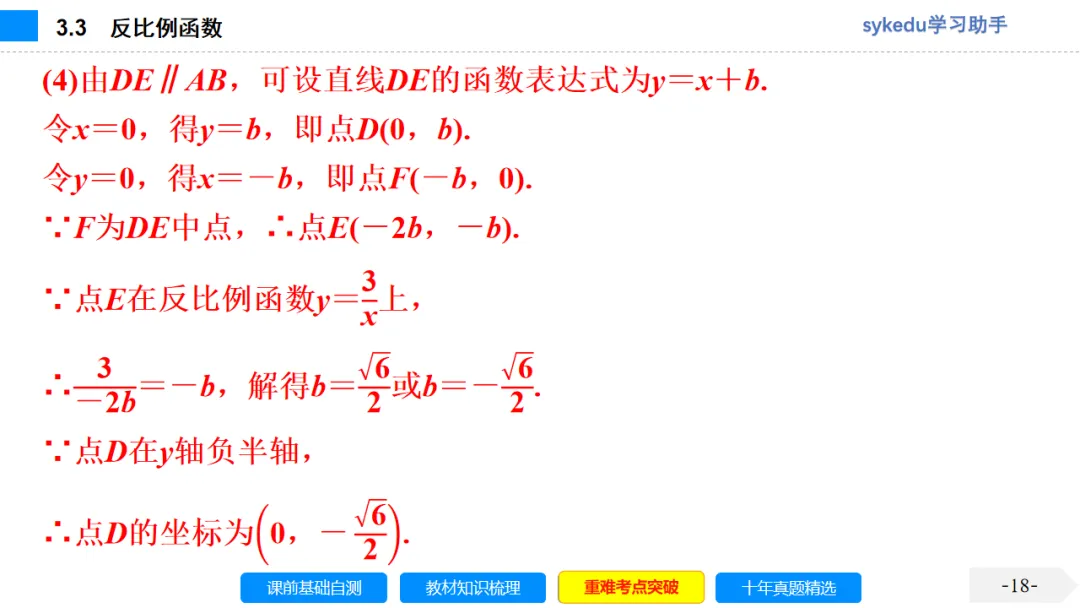
考点三 反比例函数解析式的确定
1.由于反比例函数的关系式中只有一个待定系数k,因此只需已知一组对应值就可以求出k.
2.待定系数法求解析式的步骤
(1)设出含有待定系数的函数解析式;
(2)把已知条件代入解析式,得到关于待定系数的方程;
(3)解方程求出待定系数,从而确定解析式.
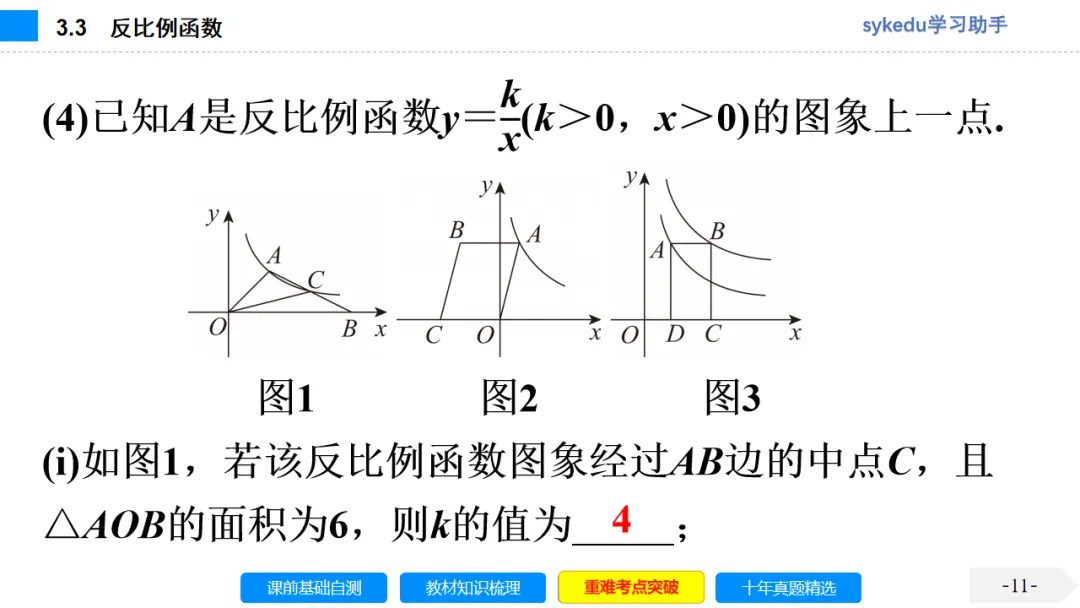
考点四 反比例函数系数k的几何意义
反比例函数y=x(k≠0)中 k的几何意义:由双曲线y=x(k≠0)上任意一点向两坐标轴作垂线,两垂线与坐标轴围成的矩形的面积为 |k|.
如图①和②,S矩形PAOB=PA·PB=|y|·|x|=|xy|=|k|,同理可得S△OPA=S△OPB=2|xy|=2|k|.
温馨提示
根据图象描述性质、根据性质大致画出图象及求解析式是一个难点,要逐步理解和掌握.
考点五 反比例函数的应用
解决反比例函数的实际问题时,要先确定函数解析式,再利用图象找出解决问题的方案,要特别注意自变量的取值范围.
















3.1 平面直角坐标系与函数-sykedu学习助手.pptx
3.4 第1课时 二次函数的图象与性质-sykedu学习助手.pptx
3.4 第2课时 二次函数性质的综合应用-sykedu学习助手.pptx






