2025年安徽省淮北市西园中学中考数学三模试卷
一、选择题(本大题共10小题,每小题4分,满分40分)每小题都给出A,B,C,D四个选项,其中只有一个是符合题目要求的.
1.(4分)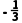 的相反数是( )
的相反数是( )
A.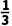 B.3C.
B.3C.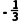 D.﹣3
D.﹣3
2.(4分)据国家统计局数据显示,2024年中国新能源汽车产量约为1316.8万辆,约占全球总量的70%.数据1316.8万用科学记数法表示为( )
A.1.3168×106B.1.3168×107
C.13.168×106D.1.3168×108
3.(4分)某几何体的三视图如图所示,该几何体是( )
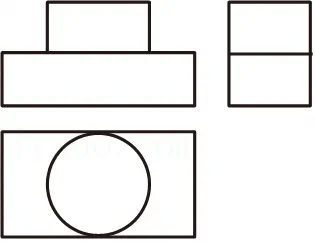

4.(4分)下列运算正确的是( )
A.a2•a3=a6B.(a2)4=a8
C.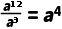 D.
D.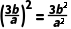
5.(4分)不等式组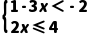 的解集在数轴上表示为( )
的解集在数轴上表示为( )
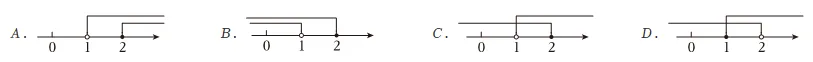
6.(4分)已知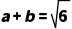 =1,则a2+b2=( )
=1,则a2+b2=( )
A.3B.4C.5D.6
7.(4分)在半径为1的⊙O中,150°的圆心角所对的弧长是( )
A.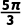 B.
B.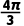 C.
C.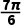 D.
D.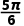
8.(4分)如图,点A,B在反比例函数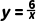 的图象上,点A,B的横坐标分别是3和6,连接OA,OB,AB,则△AOB的面积是( )
的图象上,点A,B的横坐标分别是3和6,连接OA,OB,AB,则△AOB的面积是( )
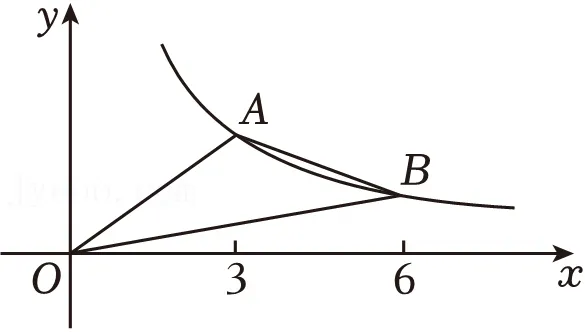
A.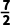 B.4C.
B.4C.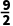 D.5
D.5
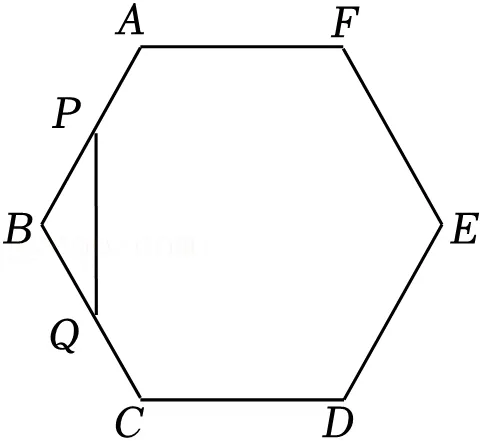
9.(4分)如图,在正六边形ABCDEF中,P,Q分别是边AB,BC的中点,连接PQ,则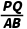 的值为( )
的值为( )
A.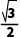 B.
B.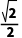 C.1D.
C.1D.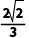
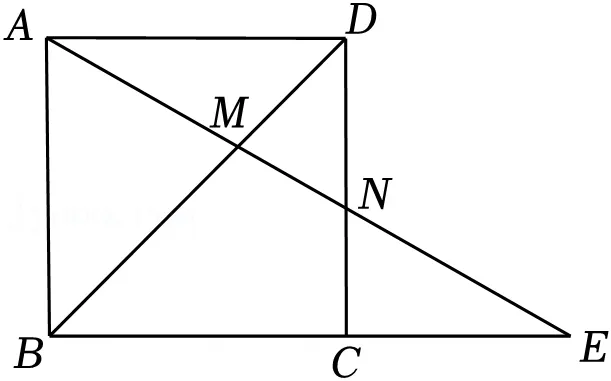
10.(4分)如图,在正方形ABCD中,E为边BC延长线上一点,连接AE,分别交DB,DC于M,N两点.若AM=NE=4,则MN的长度为( )
A.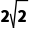 B.2C.
B.2C.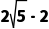 D.
D.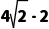
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)﹣64的立方根是 .
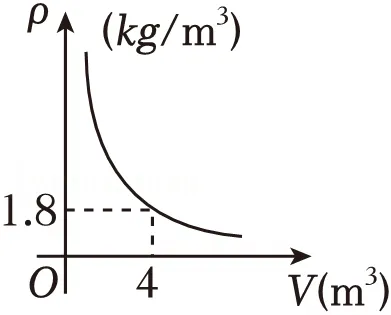
12.(5分)在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度ρ也随之改变,ρ与V在一定范围内满足关系式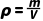 (m是常数,且m≠0),它的图象如图所示,当ρ为3.6kg/m3时,V的值为 .
(m是常数,且m≠0),它的图象如图所示,当ρ为3.6kg/m3时,V的值为 .
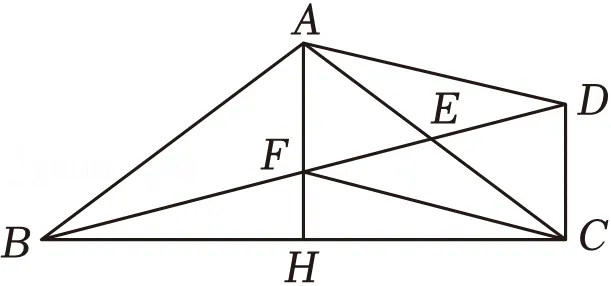
13.(5分)如图,在△ABC中,AB=AC=5,BC=8,D为△ABC外一点,AH⊥BC,DC⊥BC.连接AD,BD,CF,BD交AC于点E,且∠ADB=2∠CBD,则AD的长为 .
14.(5分)抛物线y=ax2﹣4ax经过原点,且与x轴的正半轴交于点A,顶点C的坐标为(2,﹣4).
(1)a的值为 .
(2)若P为抛物线上一动点,其横坐标为t,作PQ⊥x轴,且点Q在一次函数y=x﹣4的图象上.当1<t<4时,PQ的最大值是 .
三、(本大题共2小题,每小题8分,满分16分)
15.(8分)先化简,再求值: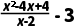 ,其中
,其中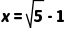 .
.
16.(8分)某手工陶器作坊制作了A,B两种型号的陶器摆件共80件,其成本和售价如下表,
型号 | 成本/(元/件) | 售价/(元/件) |
A | 40 | 70 |
B | 30 | 50 |
该手工陶器作坊销售完这批陶器摆件,获得利润2100元.分别求这批陶器摆件中A,B两种型号的数量.
四、(本大题共2小题,每小题8分,满分16分)
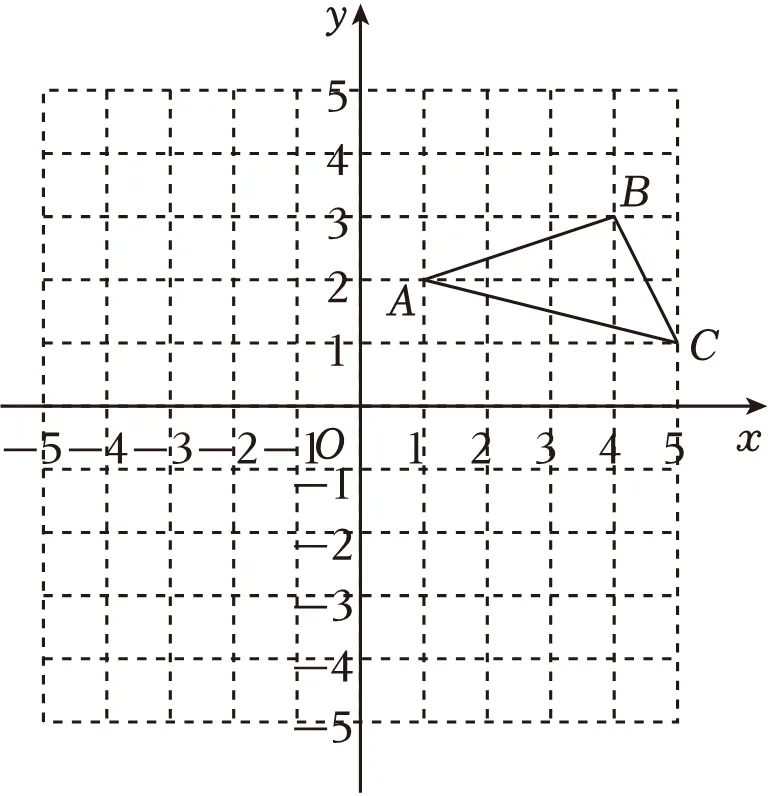
17.(8分)如图,同格中的每个小正方形的边长都是1,每个小正方形的顶点叫格点,△ABC的每个顶点都在格点上.
(1)将△ABC向左平移6个单位长度,得到△A1B1C1,画出△A1B1C1.
(2)在平面直角坐标系中,△A2B2C2与△ABC关于原点O成中心对称,请画出△A2B2C2.
(3)请在x轴上找一点P,使PA+PC的长度最短.
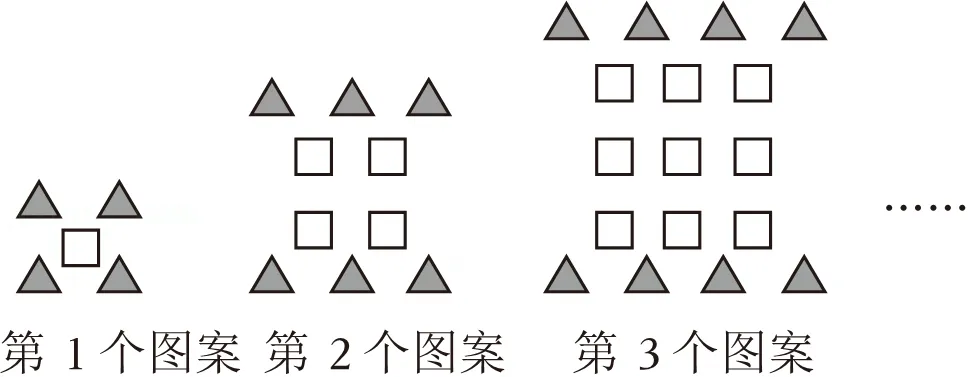
18.(8分)【观察思考】
【规律发现】
请用含n的式子填空:
(1)第n个图案中“□”的个数为 .
(2)第1个图案中“▲”的个数可表示为2×1+2,第2个图案中“▲”的个数可表示为2×2+2,第3个图案中“▲”的个数可表示为2×3+2,……,第n个图案中“▲”的个数可表示为 .
【规律应用】
(3)若第n个图案中“□”比“▲”多33个,求正整数n的值.
五、(本大题共2小题,每小题10分,满分20分)
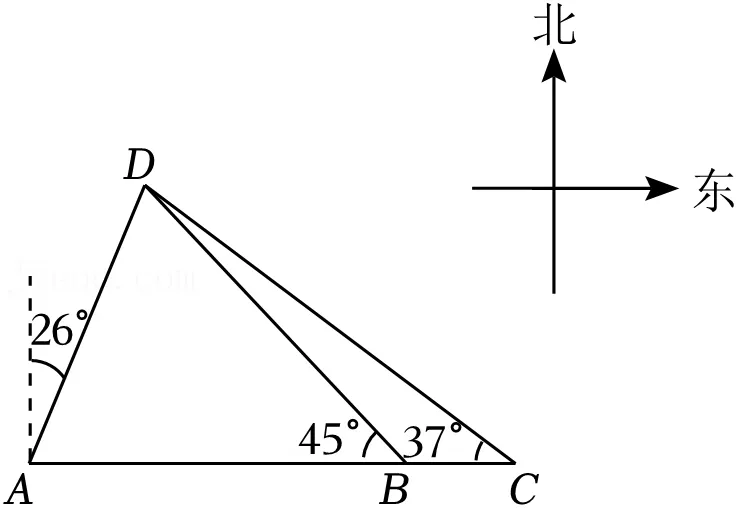
19.(10分)如图,在港口A处的正东方向有两个相距6km的观测点B,C.一艘轮船从A处出发,沿北偏东26°方向航行至D处,在B,C处分别测得∠ABD=45°,∠C=37°求轮船航行的距离AD.(参考数据:sin26°≈0.44,cos26°≈0.90,tan26°≈0.49,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
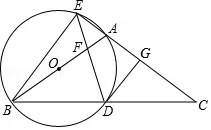
20.(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC于点D,交CA的延长线于点E,过点D作DG⊥AC,垂足为点G,连接DE,交AB于点F,连接BE.
(1)求证:DG是⊙O的切线;
(2)若AE=4,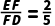 ,求BE的长.
,求BE的长.
六、(本题满分10分)
21.(10分)为了激发学生对科技的兴趣,培养创新精神,学校举办了校园科技节.期间,从全校1600名学生中抽取部分学生组织了一场科技知识竞赛(满分为100分,得分x均为不小于60的整数),并将知识竞赛成绩分为合格(60≤x<70)、一般(70≤x<80)、良好(80≤x<90)、优秀(90≤x≤100)四个等级,并将结果制作成如下统计图(部分信息未给出).
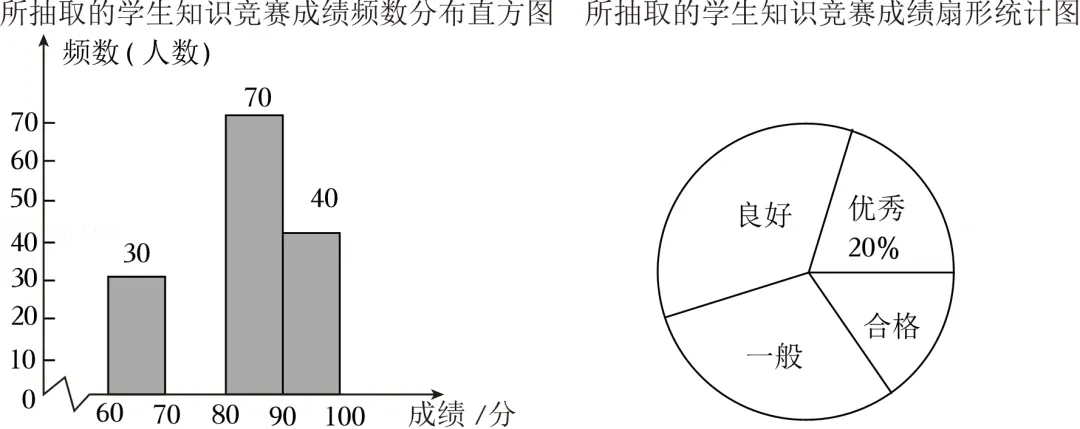
请根据以上信息,解答下列问题:
(1)补全频数分布直方图.
(2)扇形统计图中“一般”等级所对应的扇形的圆心角度数为 .
(3)这次知识竞赛成绩的中位数落在 等级.(填写“合格”“一般”“良好”或“优秀”)
(4)若全校学生都参加知识竞赛,请根据抽样成绩的结果,试估计该校知识竞赛成绩为80分及以上的学生人数.
七、(本题满分12分)
22.(12分)如图1,在凸五边形ABCDE中,AB=AE,BC=DE,BD与CE相交于点F,AC=AD.
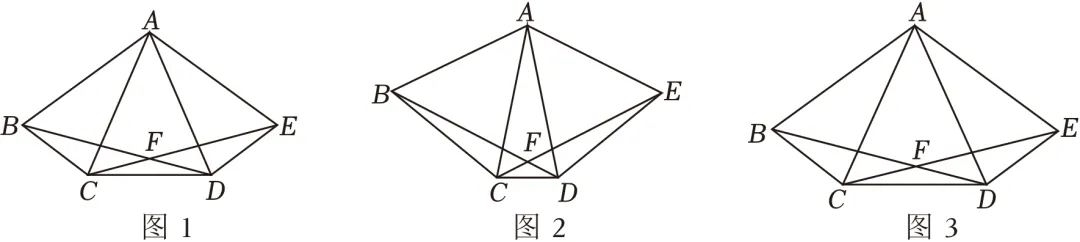
(1)求证:∠BAD=∠CAE.
(2)如图2,当∠ADB=∠BAC时,求证:AB=BF.
(3)如图3,若AB=AC=2BC,且AB∥DE时,请直接写出tan∠ACE的值.
八、(本题满分16分)
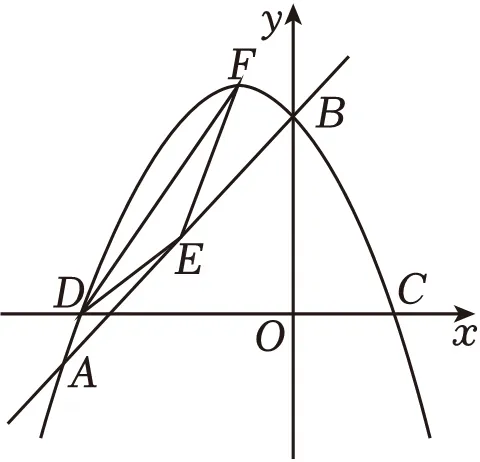
23.(16分)如图,在平面直角坐标系中,直线y=kx+4(k≠0)与抛物线y=ax2+bx+4相交于点A,与y轴相交于点B(0,4),抛物线与x轴的两个交点分别为点C(2,0),D(﹣4,0).
(1)求a,b的值;
(2)当﹣4≤x≤t时,y的最大值与最小值的差为4.5,求t的取值范围;
(3)若E为线段AB的中点,且点E在第二象限内,F为抛物线的顶点,当△DEF的面积最小时,求k的值.
2025年安徽省淮北市西园中学中考数学三模试卷
参考答案与每一道试题解析见网盘免费下载

我用夸克网盘给你分享了「2025年安徽省宣城市宁国中学自主招生数学试卷.docx」,点击链接或复制整段内容,打开「夸克APP」即可获取。
/~783d3LVicy~:/
链接:https://pan.quark.cn/s/a65f822374b9?pwd=hz9q
提取码:hz9q






