中考数学提分:旋转常考5大模型

【中考数学提分：旋转常考5大模型】

一、旋转模型的核心本质

旋转模型是初中几何的明珠，其本质是通过图形绕定点旋转特定角度（常见60°或90°），构造全等或相似三角形。这种动态变换犹如魔术师的手法，能将分散的条件集中，让隐藏的几何关系浮出水面。

二、四大经典模型详解

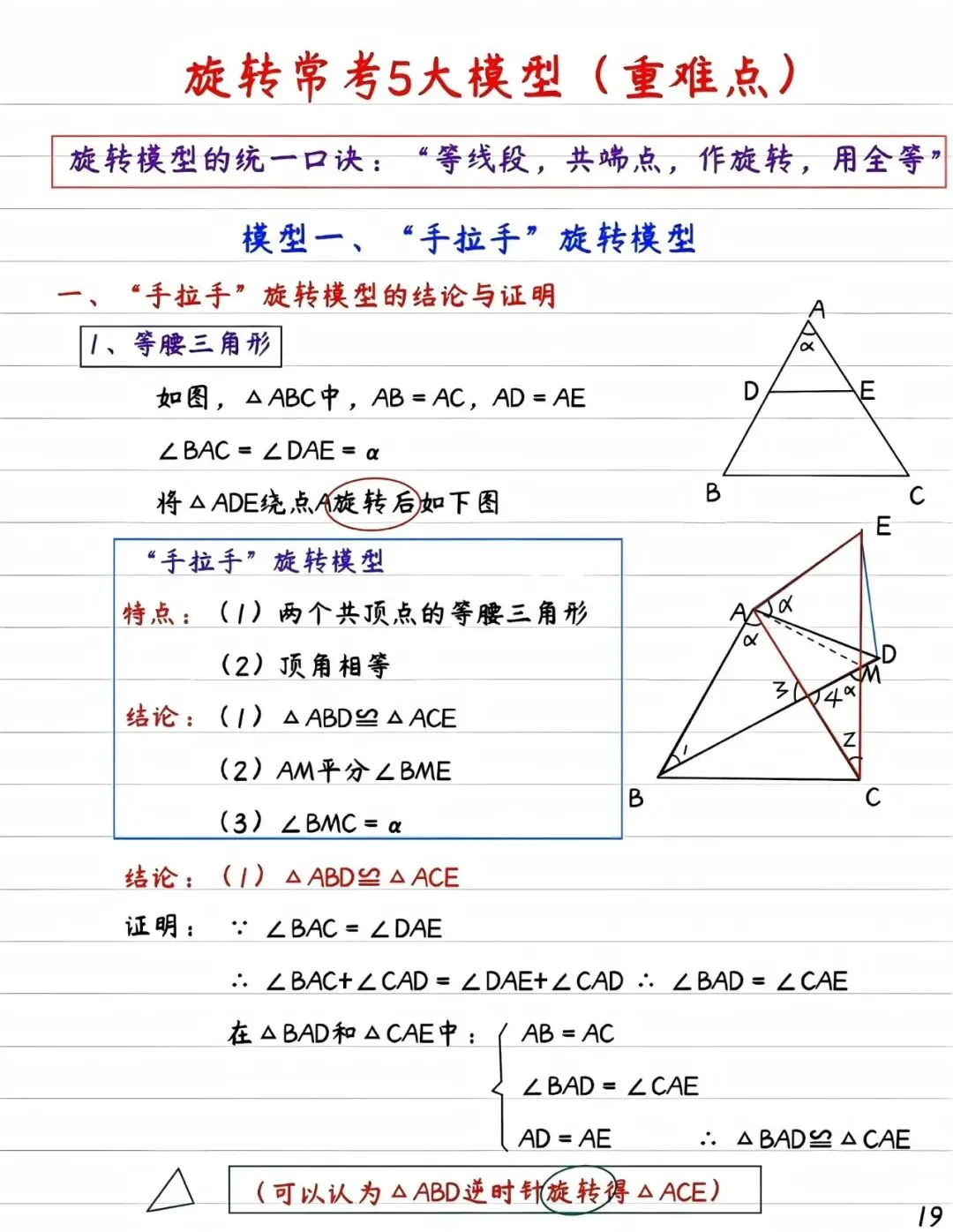
1. 共顶点旋转（手拉手模型）

当两个等腰三角形共享顶点时，旋转会产生"孪生三角形"。例如△ABC绕顶点A旋转60°，新形成的△ADE与△ABC就像双胞胎，对应边夹角恒等于旋转角。

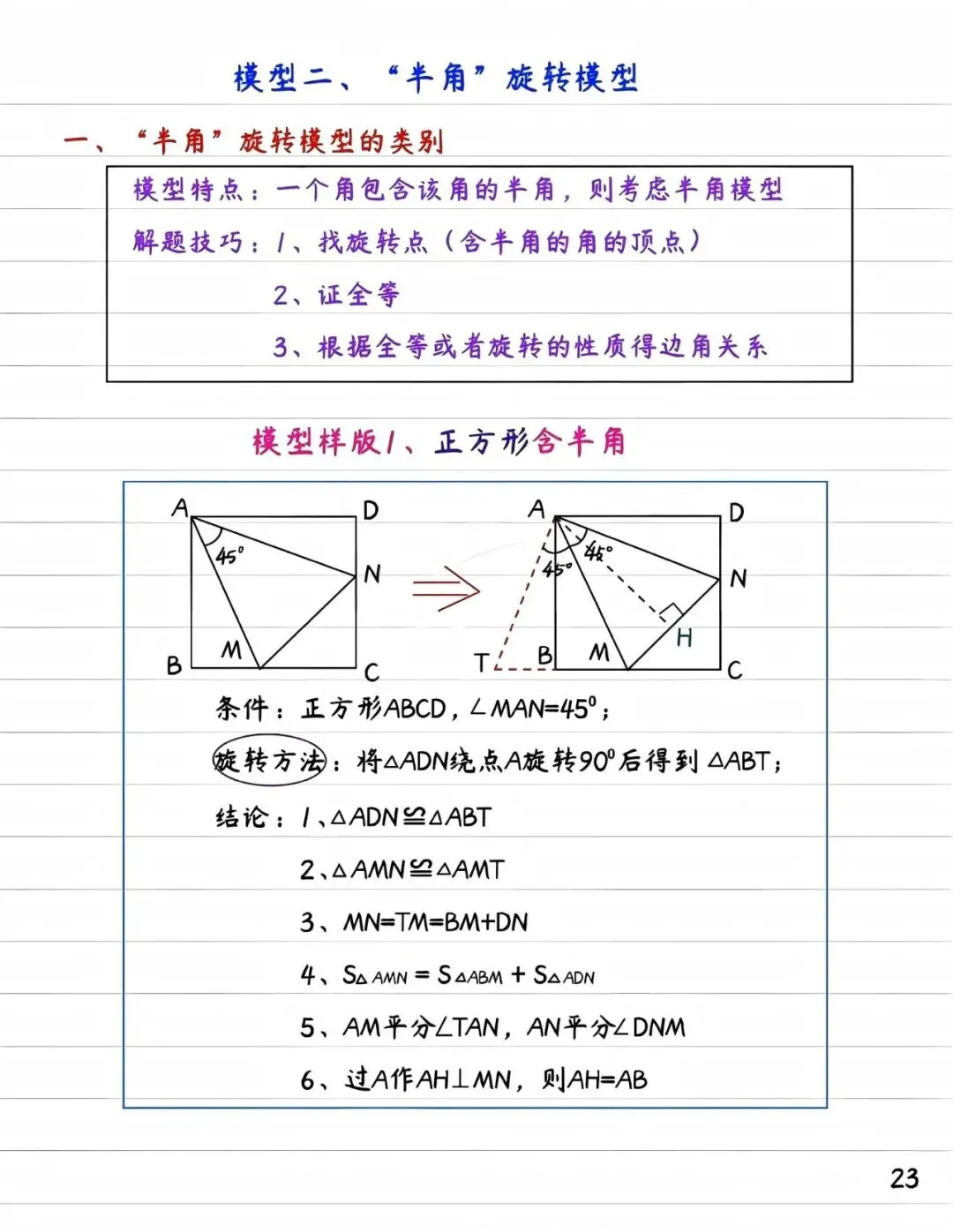
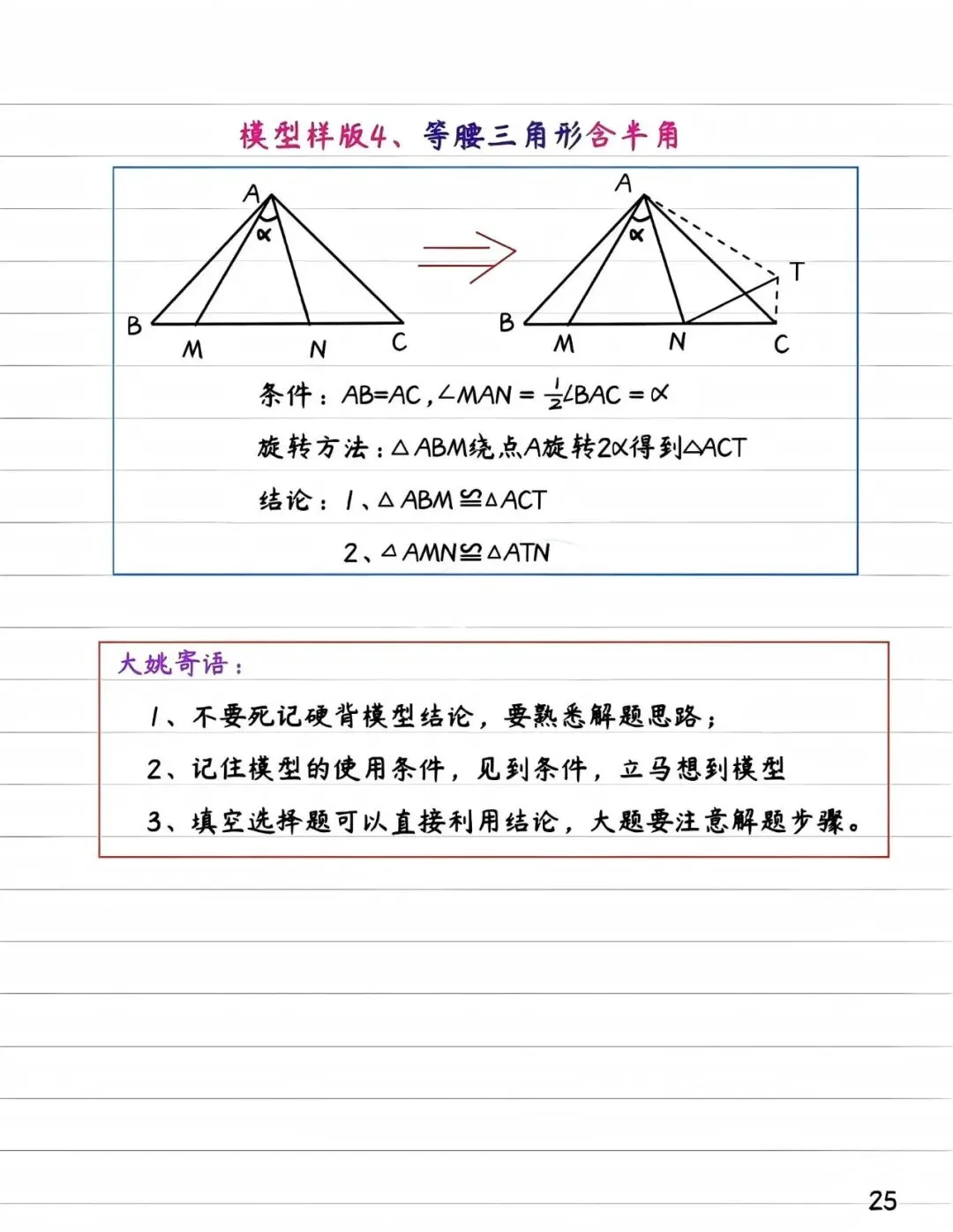
2. 半角模型

45°旋转堪称解题利器。将含半角（22.5°）的三角形部分旋转，补全为完整直角，犹如拼图完成关键一块，立即显现边角关系。

3. 对角互补模型

当四边形对角和为180°时，旋转其中一三角形，会产生蝴蝶振翅般的对称效果，使对边长度、角度关系一目了然。

4. 费马点问题

通过120°旋转构造等边三角形，如同用圆规画出完美轨迹，最终找到点到三顶点的最短距离和。

三、解题三板斧

1. 旋转标记法：用彩色笔标注旋转前后的对应点，像给几何图形贴上导航标签。

2. 辅助线口诀："遇中点，想旋转；见半角，转补全"。

3. 逆向验证：旋转后务必检查对应边夹角是否等于旋转角，这是避免"镜中花"式错误的关键。

四、实战技巧

当题目出现"等腰"、"等边"、"正方形"等关键词时，旋转的号角已经吹响。记住：旋转不是目的，构造全等三角形才是终极目标。解题时建议先画出旋转前后的对比图，让几何关系像电影分镜般清晰呈现。