n

专题02 整式及因式分解
考点01 幂的运算
1.(2025·黑龙江·中考真题)下列运算正确的是()
A.B.
C.D.
2.(2025·安徽·中考真题)下列计算正确的是()
A.B.
C.D.
3.(2024·四川攀枝花·中考真题)计算的结果是()
A.B.C.D.
4.(2024·江苏苏州·中考真题)计算:.
5.(2024·黑龙江哈尔滨·中考真题)定义新运算:,则的运算结果是.
6.(2023·江苏南京·中考真题)计算的结果是.
考点02 整式的概念
1.(2023·河北·中考真题)代数式的意义可以是()
A.与x的和B.与x的差C.与x的积D.与x的商
2.(2023·江西·中考真题)单项式的系数为.
3.(2024·山东泰安·中考真题)单项式的次数是.
4.(2024·重庆·中考真题)已知整式,其中为自然数,为正整数,且.下列说法:
①满足条件的整式中有5个单项式;
②不存在任何一个,使得满足条件的整式有且只有3个;
③满足条件的整式共有16个.
其中正确的个数是( )
A.0B.1C.2D.3
5.(2025·上海·中考真题)用代数式表示与差的平方,正确的是()
A.B.C.D.
考点03 整式的运算
1.(2025·陕西·中考真题)计算的结果为()
A.B.C.D.
2.(2023·青海西宁·中考真题)计算:.
3.(2023·陕西·中考真题)计算:()
A.B.C.D.
4.(2025·四川南充·中考真题)计算:.
5.(2024·甘肃兰州·中考真题)计算:()
A.aB.C.D.
6.(2024·重庆·中考真题)计算:
(1);
(2).
7.(2023·河南·中考真题)(1)计算:;
(2)化简:.
8.(2023·湖北·中考真题)(1)计算:;
(2)解分式方程:.
9.(2025·甘肃兰州·中考真题)计算: .
10.(2025·天津·中考真题)计算的结果为.
11.(2023·四川攀枝花·中考真题)我们可以利用图形中的面积关系来解释很多代数恒等式.给出以下4组图形及相应的代数恒等式:
①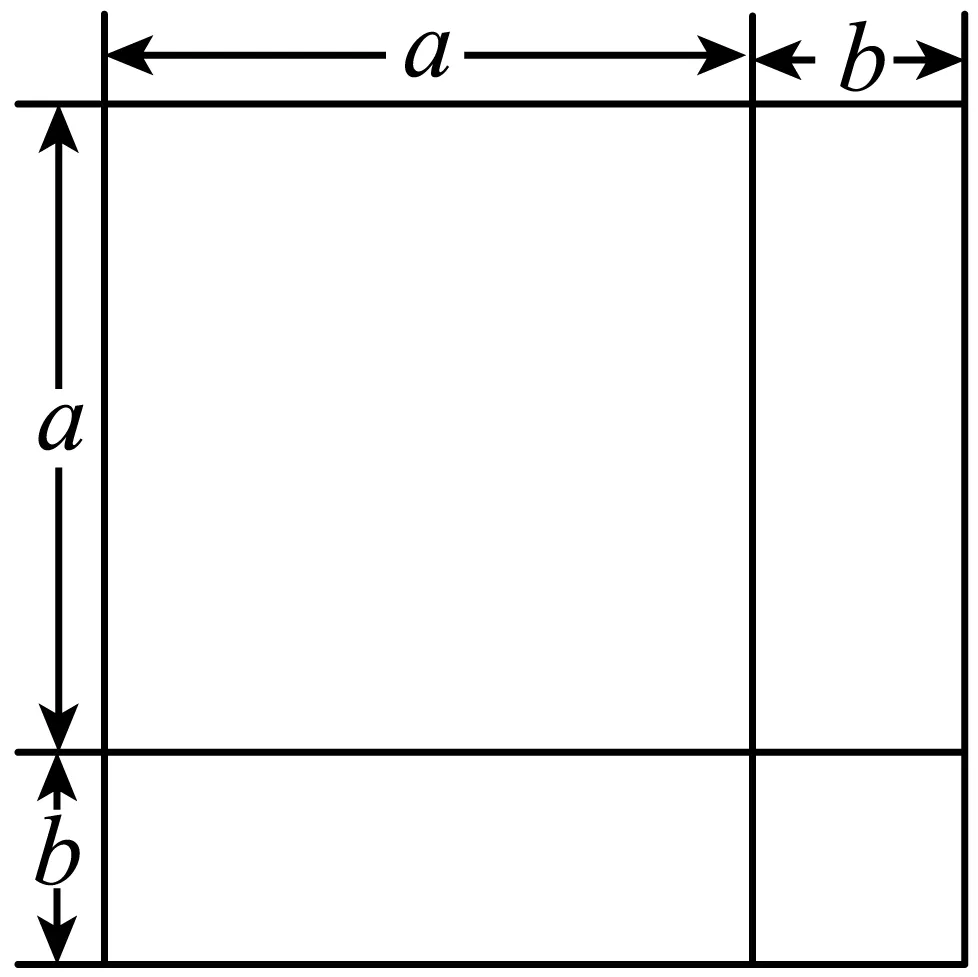 ②
②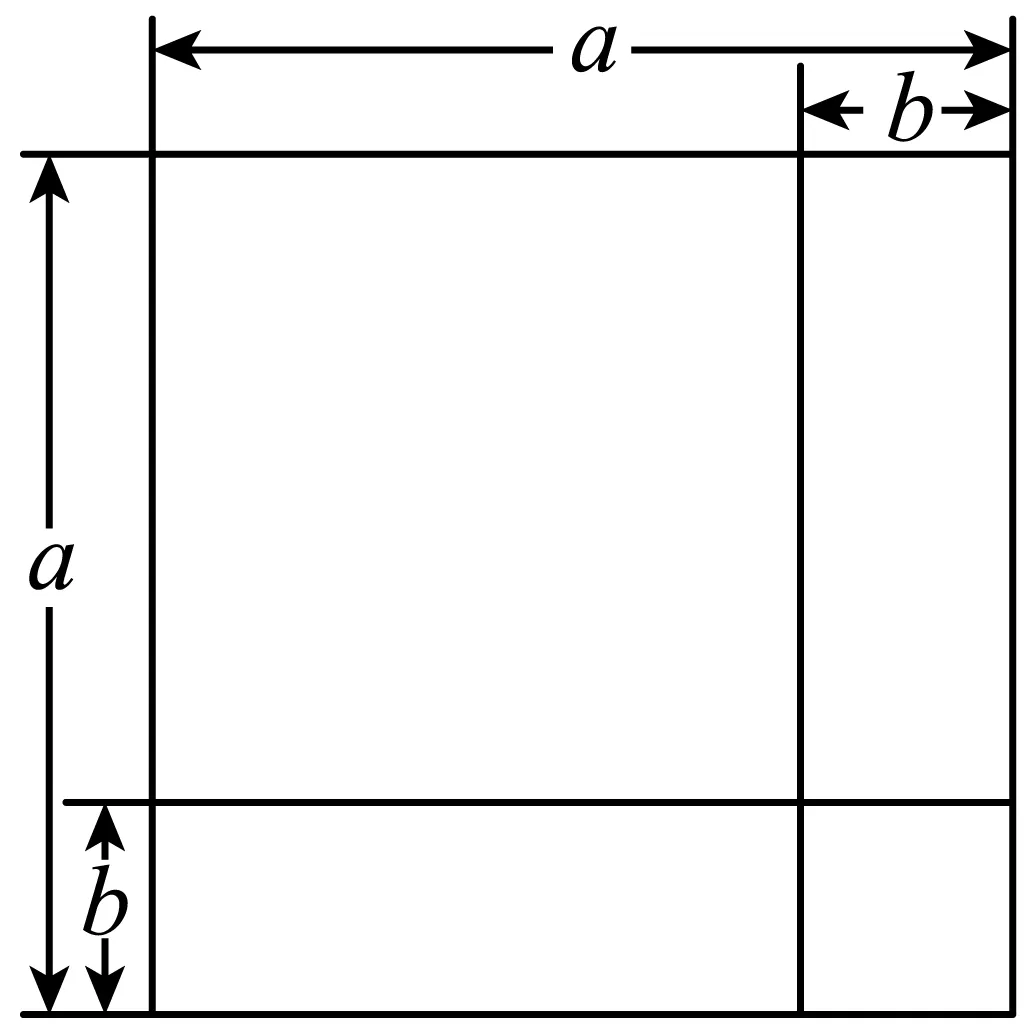
③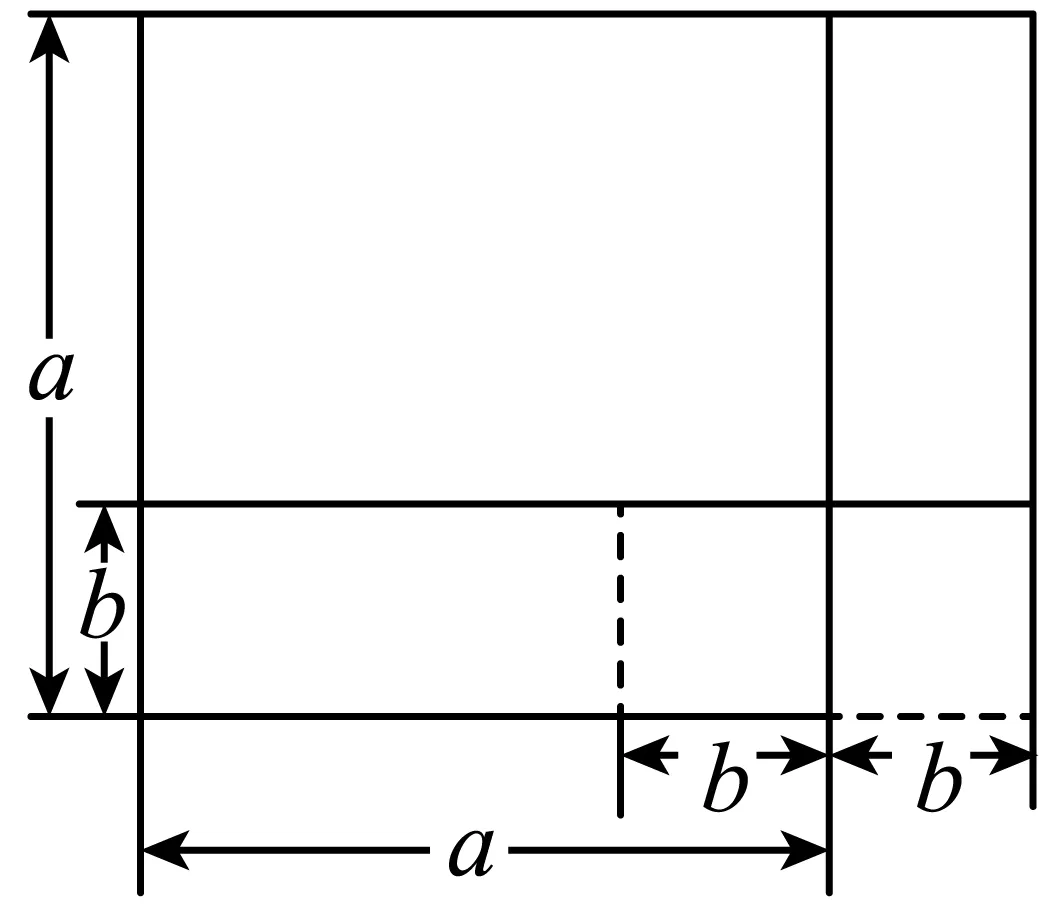 ④
④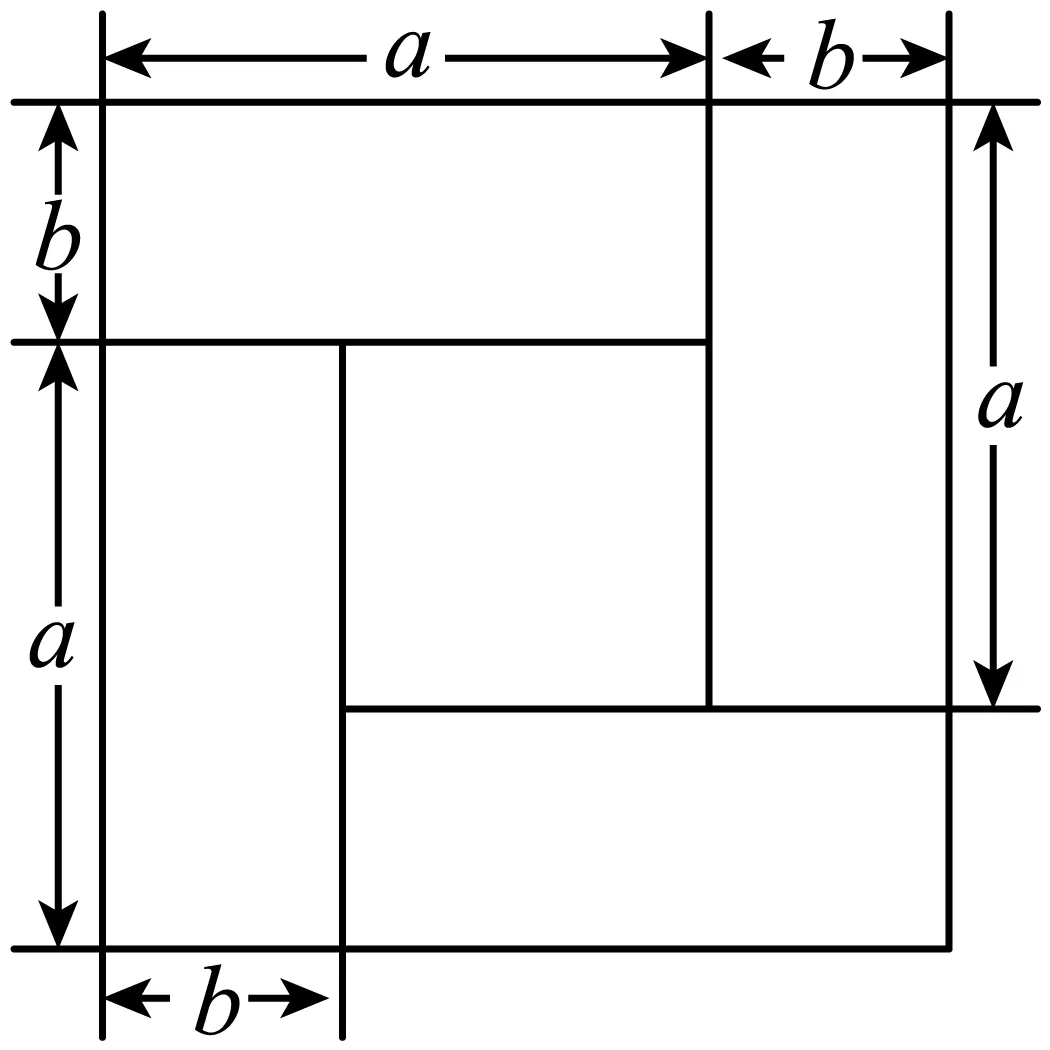
其中,图形的面积关系能正确解释相应的代数恒等式的有()
A.1个B.2个C.3个D.4个
12.(2024·江苏无锡·中考真题)计算:
(1);
(2).
13.(2023·青海西宁·中考真题)计算:.
考点04 整式的化简求值
1.(2025·浙江·中考真题)化简求值:,其中.
2.(2023·江苏·中考真题)若,则的值是.
3.(2023·江苏·中考真题)先化简,再求值:,其中.
4.(2023·湖南·中考真题)先化简,再求值:,其中.
5.(2025·湖南·中考真题)先化简,再求值:,其中.
6.(2024·甘肃·中考真题)先化简,再求值:,其中,.
7.(2023·四川凉山·中考真题)先化简,再求值:,其中,.
考点05 代数式中的规律
1.(2025·陕西·中考真题)生活中常按图①的方式砌墙,小华模仿这样的方式,用全等的矩形按规律设计图案,如图②,第1个图案用了3个矩形,第2个图案用了5个矩形,第3个图案用了7个矩形,……则第10个图案需要用矩形的个数为.

2.(2025·黑龙江绥化·中考真题)观察下图,图(1)有2个三角形,记作;图(2)有3个三角形,记作;图(3)有6个三角形,记作;图(4)有11个三角形,记作;按此方法继续下去,则(结果用含的代数式表示).

3.(2024·四川成都·中考真题)在综合实践活动中,数学兴趣小组对这个自然数中,任取两数之和大于的取法种数进行了探究.发现:当时,只有一种取法,即;当时,有和两种取法,即;当时,可得;…….若,则的值为;若,则的值为.
4.(2023·山东临沂·中考真题)观察下列式子
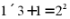
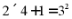
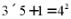
……
按照上述规律,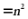
5.(2023·湖南岳阳·中考真题)观察下列式子:
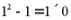
依此规律,则第(为正整数)个等式是.
6.(2025·新疆·中考真题)对多项式A,B,定义新运算“”:;对正整数k和多项式A,定义新运算

通过网盘分享的文件:三年(2023-2025)中考真题分类汇编(全国通用)
链接: https://pan.baidu.com/s/1489j7ii8Wz9ALgJ8AqGKCg?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享





