2.1一次方程(组)及其应用-初中数学中考-最新中考复习-sykedu学习助手-第一部分 安徽考点探究

第二章方程（组）与不等式（组）

第一节　一次方程(组)及其应用 - 考点知识梳理

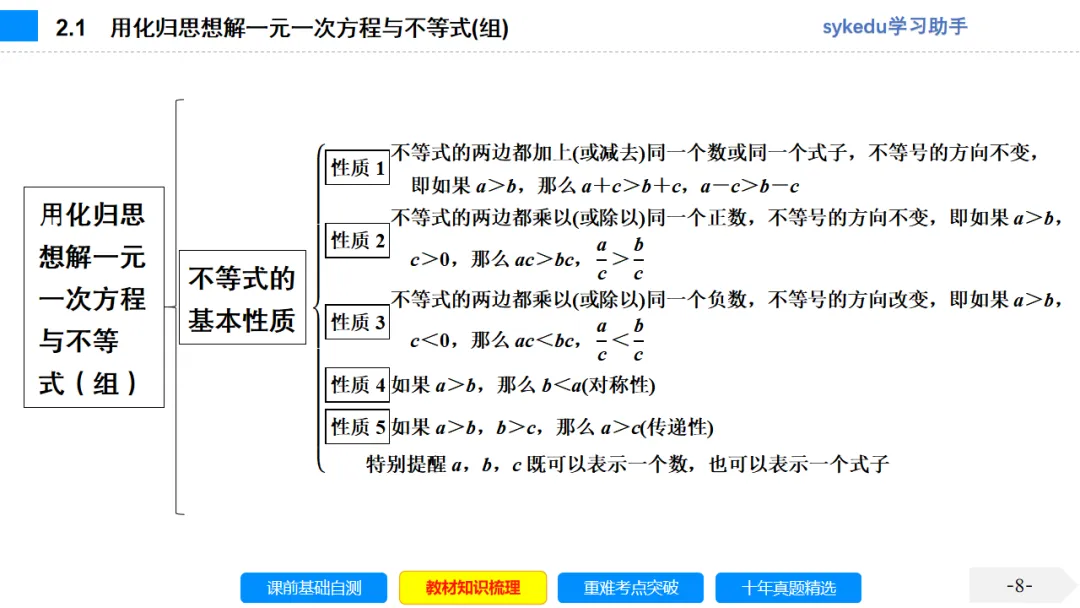
考点一  等式的性质及方程的有关概念

1．等式的性质

性质1：等式的两边都加上(或减去)同一个数(或式子)，所得的结果仍是等式．即如果a＝b，那么a±c＝b±c.

性质2：等式的两边都乘(或除以)同一个不为0的数(或式子)，所得的结果仍是等式．即如果a＝b，那么ac＝bc或c(a)＝c(b)(c≠0).

2．方程：含有未知数的等式叫做方程．

考点二        一元一次方程

1．一元一次方程

在整式方程中，只含有一个未知数(元)，并且未知数的次数都是1，这样的方程叫做一元一次方程．一元一次方程的标准形式是 ax＋b＝0(a≠0).

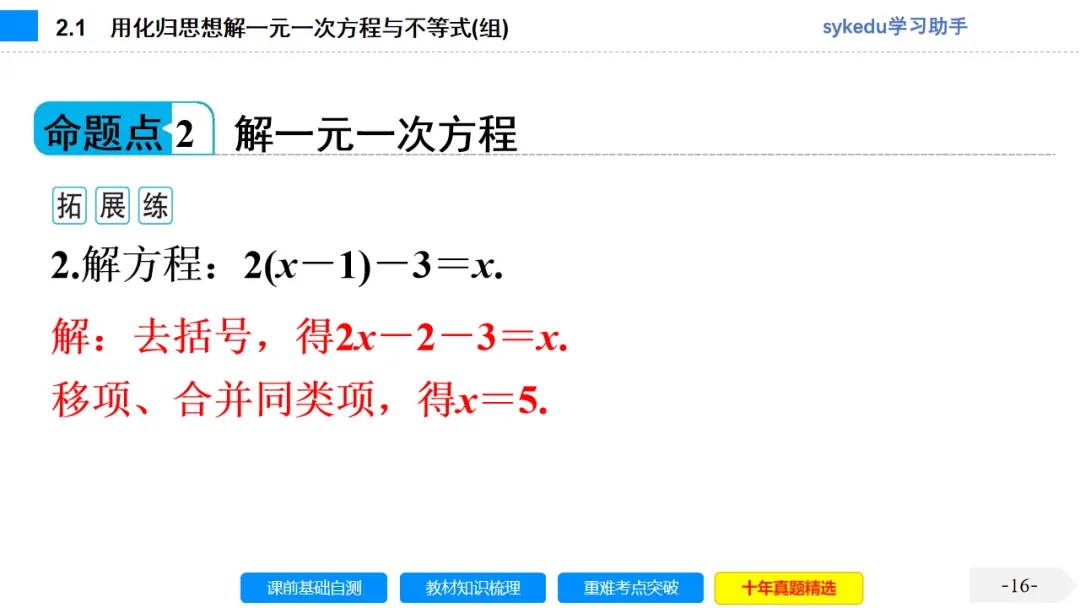
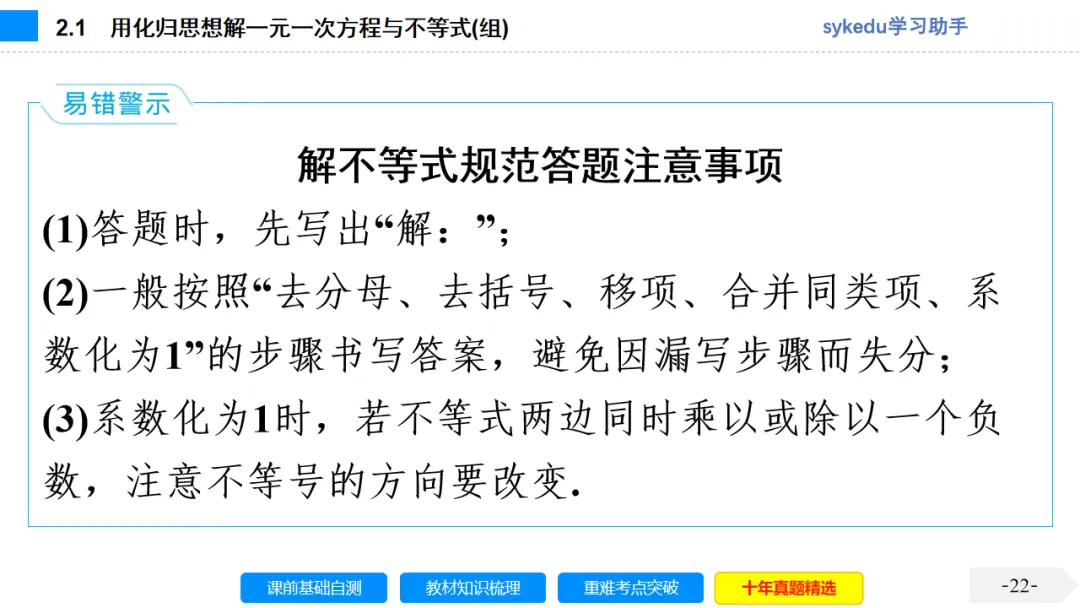
2．解一元一次方程的一般步骤

(1)去分母；(2)去括号；(3)移项；(4)合并同类项；(5)系数化为1.

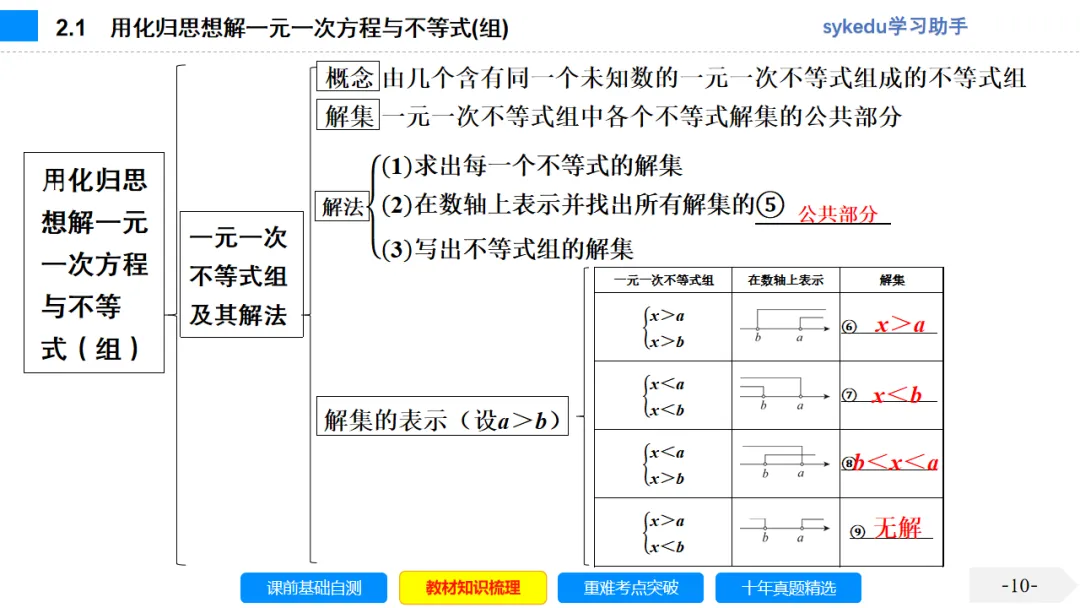
考点三          二元一次方程组及解法

1．二元一次方程组

(1)二元一次方程的一般形式：ax＋by＋c＝0(a，b，c是常数，且a≠0，b≠0)．

(2)两个含有相同未知数的二元一次方程合在一起，构成二元一次方程组．

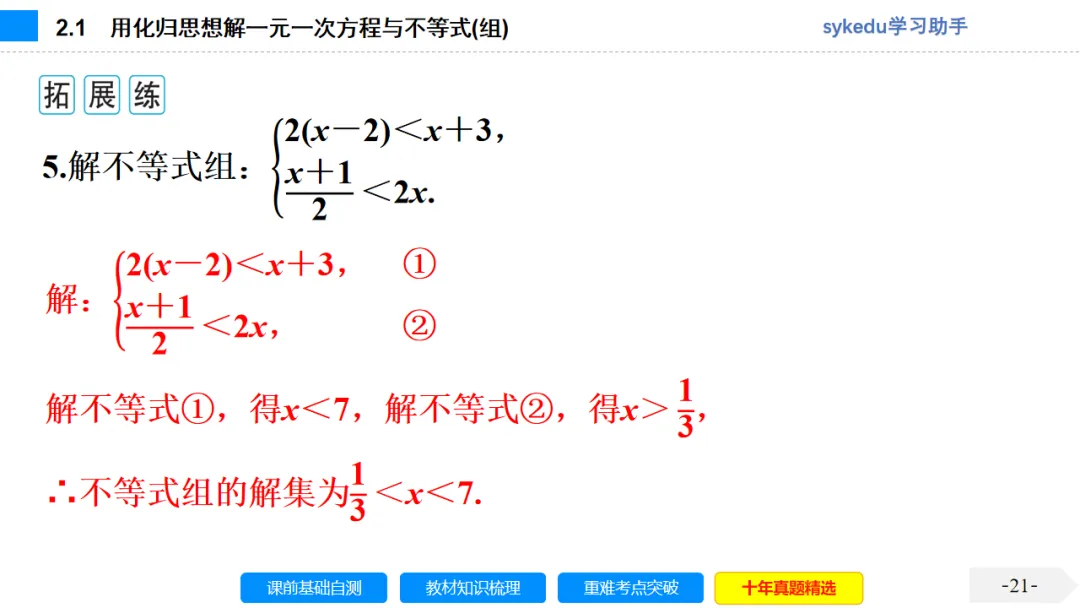
2．解二元一次方程组的基本思路：消元．

3．二元一次方程组的解法：(1)代入消元法；(2)加减消元法；(3)图象法．

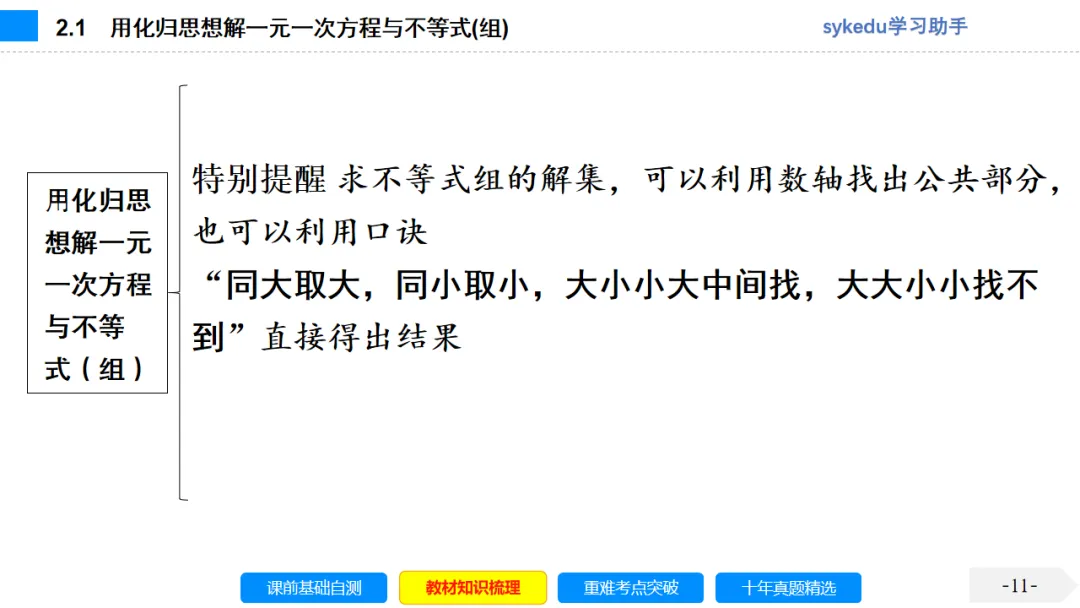
温馨提示

当方程组中一个方程的某个未知数的系数的绝对值为1时，用代入消元法较为简单；当方程组中两个方程的某个未知数的系数的绝对值相等或成倍数关系时，用加减消元法较为简单.

考点四       三元一次方程组的定义与解法（选学）

1．三元一次方程组：方程组中含有三个相同的未知数，每个方程中含未知数的项的次数都是1，并且一共有三个方程，像这样的方程组叫做三元一次方程组．

2．解三元一次方程组的一般步骤：三元一次方程组消元(――→)二元一次方程组消元(――→)一元一次方程．

考点五       列一次方程 (组)解应用题

1．列一次方程(组)解应用题的一般步骤

(1)弄清题意，搞清楚条件是什么，求什么．

(2)设未知数：

(3)找出能够包含未知数的等量关系；

(4)列出方程(组)．

(5)求出方程(组)的解．

(6)检验(看是否符合题意)．

(7)写出答案(包括单位名称)．

2．列一次方程(组)解应用题的关键是：确定等量关系．

3．应用题中常见的数量关系及题型

(1)数字问题(包括日历中的数字规律)

①设个位数字为c，十位数字为b，百位数字为a，则这个三位数是100a＋10b＋c；

②日历中前后两日差1，上下两日差7.

(2)体积变化问题

(3)打折销售问题      ①利润＝售价－成本；②利润率＝ 成本　(利润)×100%.

(4)行程问题      路程＝速度×时间.

若用v表示轮船的速度，用v_顺、v_逆、v_水分别表示轮船顺水、逆水和水流的速度，则有如下关系：

v_顺＝v＋v_水v_逆＝v－v_{水    v}＝2(v顺＋v逆)v_水＝2(v顺－v逆)

在轮船航行问题中，知道v_顺、v_逆、v、v_水中的任何两个量，总能求出其他的量．

(5)储蓄问题

①利息＝本金×利率×期数；

②本息和＝本金＋利息＝本金×(1＋利率×期数)．