

广东中考数学压轴题,
为何年年都是初三的“失分重灾区”?
核心考点到底有哪些、哪些题型年年必考?
一. 高频考点与题型
1、几何综合(占比约50%):
(1)动态几何(旋转、折叠、平移)与坐标系结合,如正方形旋转后点的坐标计算、折叠后点的轨迹分析。
(2)圆与三角形综合题:切线性质、圆周角定理、垂径定理的应用(如2017、2018、2023年题)。
(3)特殊四边形(矩形、正方形)的性质与判定,常涉及对称性和面积最值。
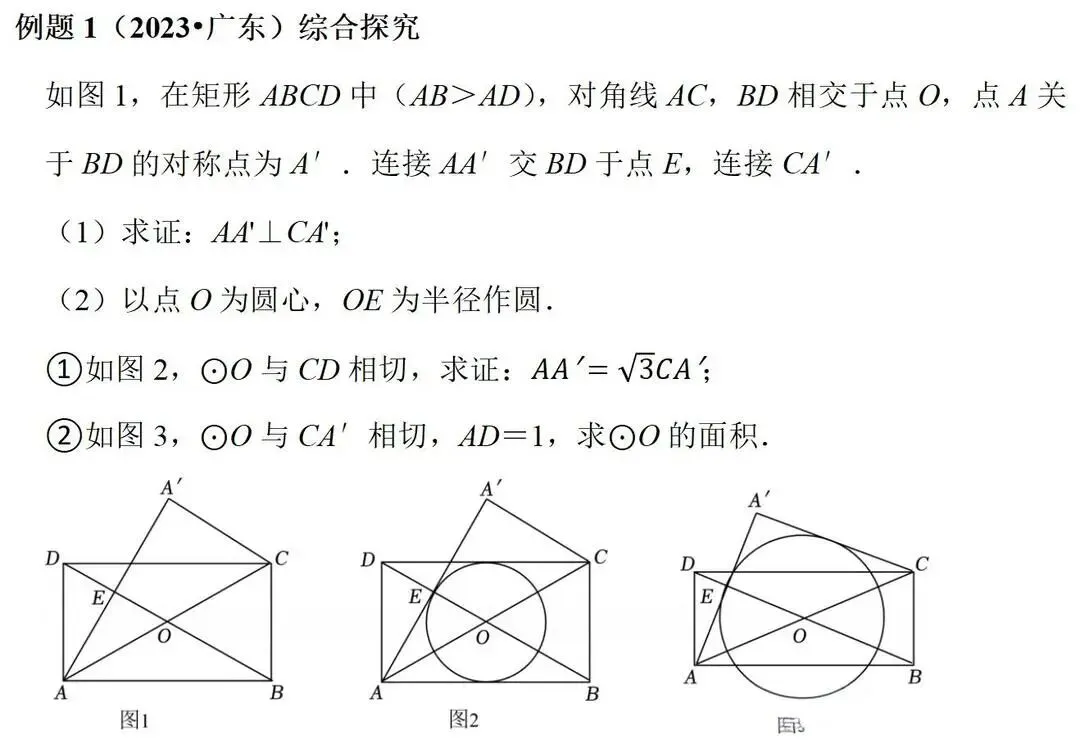
2、函数综合(占比约40%):
(1)二次函数与几何结合:求解析式、对称轴、顶点坐标,与直线交点问题(如2016、2020、2022年题)。

(2)反比例函数与一次函数交点及不等式问题(如2019、2020年题)。
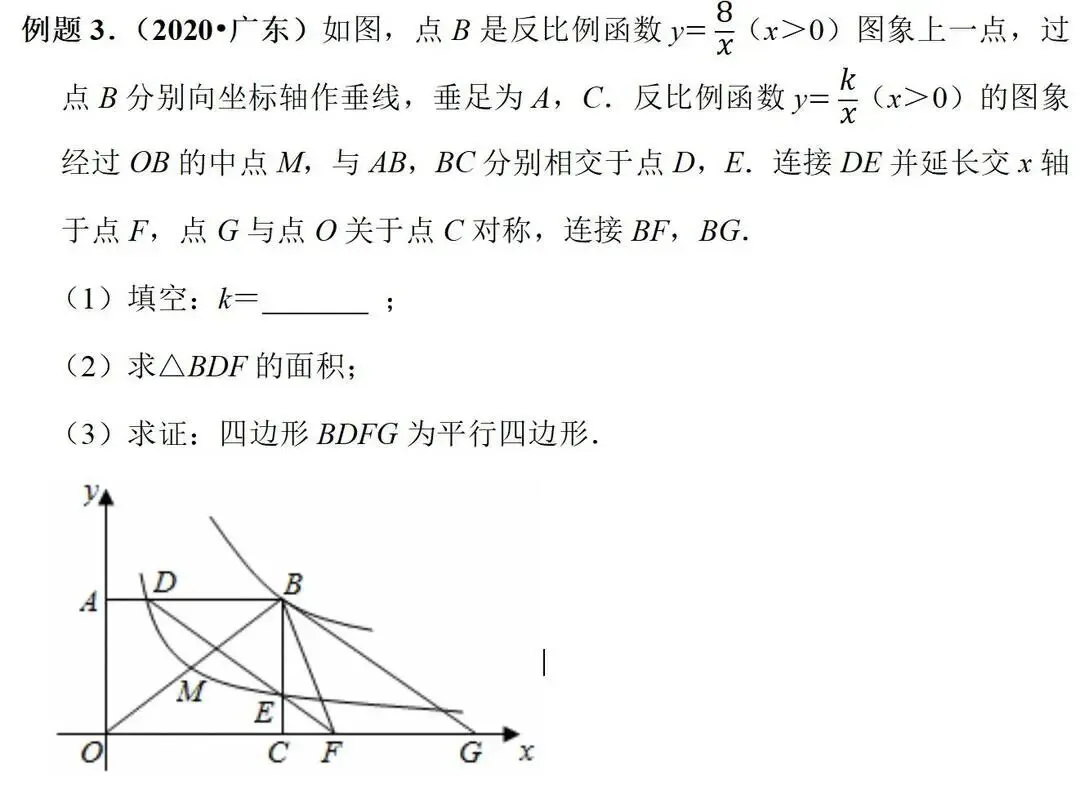
(3)动态函数关系:通过几何变换(如旋转)导出函数表达式(如2023年题)。
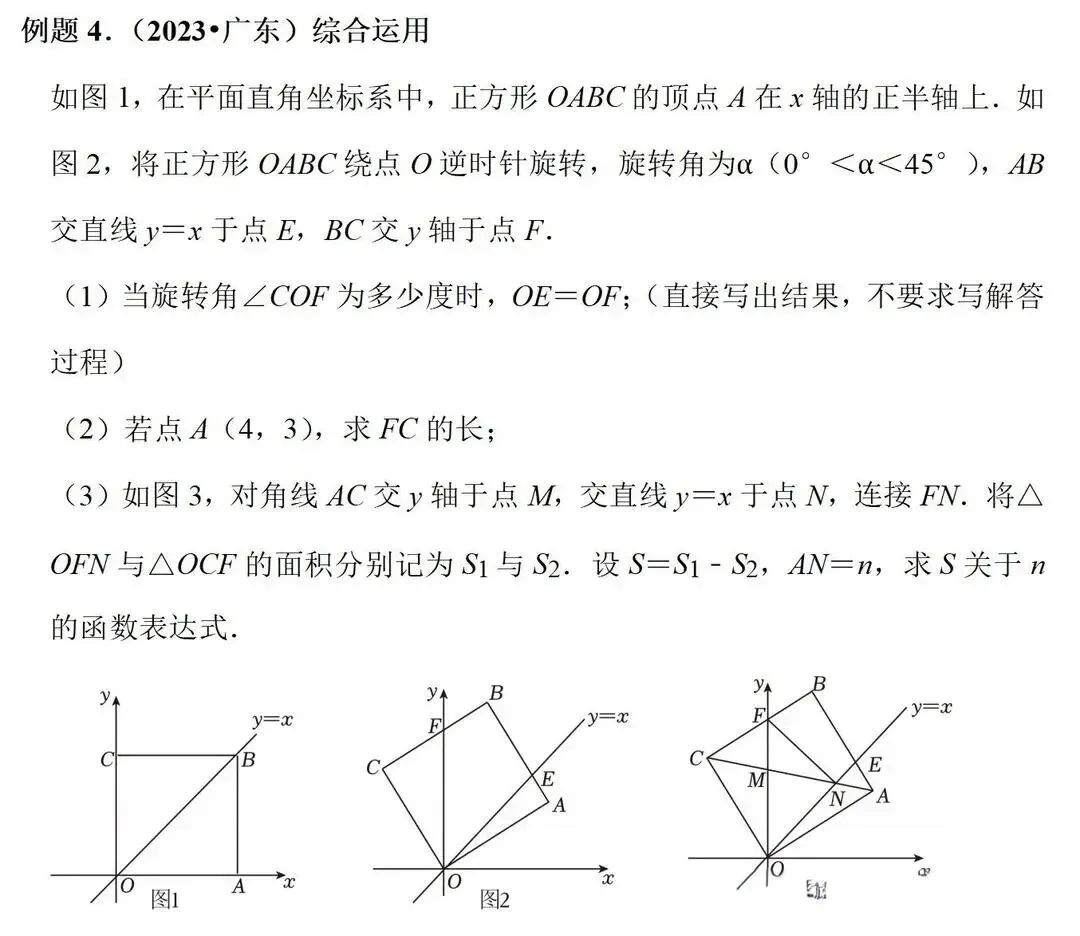
3、存在性问题与最值问题(占比约10%):
(1)平行四边形、相似三角形的存在性判定(如2021年题);
(2)线段长度、面积、角度的最值问题(如2022年题)。
二. 同一题型未考到的潜在考点
1、几何方面:
(1)立体几何(三视图、球体或棱柱体积计算);
(2)解析几何中的非圆二次曲线(椭圆、双曲线);
(3)复杂轨迹问题(如圆锥曲线的生成)。
2、代数方面:
(1)高次方程或分式方程的特殊解;
(2)数列与函数结合的实际应用题。
3、综合应用:
(1)跨学科实际模型(如物理运动中的抛物线);
(2)新定义题型(如自定义几何变换规则)。
备注:这些知识点考到的可能性极小。
三. 2026年压轴题预测
1、题型:动态几何与二次函数综合题。
2、考点:
(1)动态几何 + 抛物线 + 尺规作图:折叠 / 旋转图形与抛物线结合,融入尺规作图(如黄金分割、角平分线作图),要求结合相似三角形判定求点坐标、推导线段关系,兼顾几何直观和运算能力;
(2)含参二次函数的代数推理 + 最值:强化含参变量的二次函数推导,结合几何图形的面积 / 线段最值,要求严谨的代数推理步骤,分类讨论参数取值范围,杜绝漏解;
(3)新定义综合题:自定义几何变换 / 函数规则(如 “中外比点”“子抛物线”),结合教材拓展内容(如黄金分割、勾股定理拓展),考查快速“翻译”新定义、转化为常规题型的能力。
四. 备考建议
1. 夯实核心基础,强化经典模型
✅ 整理几何综合经典模型:动态几何(旋转 / 折叠 / 平移)的“变中不变”思想是关键,总结全等 / 相似、对称性、轨迹分析的解题技巧,熟练掌握圆、特殊四边形的核心性质;
✅ 补全冷门考点盲区:针对性练习尺规作图(黄金分割、角平分线、垂直平分线)、分式方程(无解讨论)、命题真假判断等知识点,避免基础题失分;✅ 熟练函数基础推导:二次函数解析式、对称轴、顶点坐标的推导做到零失误,掌握反比例与一次函数的交点、不等式求解的常规方法。2. 突破压轴难点,训练高阶能力
3. 适应新考向,提升综合素养
✅ 吃透新定义题型:训练快速阅读、理解新定义的能力,学会将陌生定义转化为常规数学知识,不被新名词吓住,按题目要求一步步推导;
✅ 提升情境化解题能力:多做结合生活、文化、跨学科的情境题,学会从题干中提取有效数学信息,建立数学模型,解决实际问题;
✅ 规范解题书写:尤其是尺规作图、代数推理、新定义证明题,书写步骤要规范、清晰,避免因步骤跳跃、逻辑断裂导致的失分。

距离数学中考仅剩 137 天,备考的关键不是刷遍所有题,而是吃透十年真题规律,夯实核心考点,针对性突破 2025 新考向,基础题保满分、中等题不丢分、压轴题多拿分,就能在数学考试中脱颖而出!
评论区聊聊:你最担心数学哪个题型?评论区留言,一起交流解题技巧!

插播一条重要消息!
26中考签约mk好消息【公费生,半公费生,奖学金生,优待生】等福利政策🌟🌟
1️⃣🚀DH/JW/HL/HW 四大名校升学唯一降分录取优先第1️⃣志愿上岸||签约满足保高中三年顶配班型和公费生待遇。
2️⃣第一批次活动报名马上截止,速速登记签约指标🈶限制人满停止⚠️
乐思培优6大校区:公益深度链接高中名校升学资源,100%值得信赖❗️

欢迎大家添加彭校微信
发送孩子【学校+年级】
拉你进东莞小升初MK群、TY群
抢先了解更多🌹🌹🌹





——往期推荐——







