1.3分式-初中数学中考-最新中考复习-sykedu学习助手-第一部分 安徽考点探究

第一章　数与式（文章最后有电子版资源供大家免费下载）

第三节　分式 - 考点知识梳理

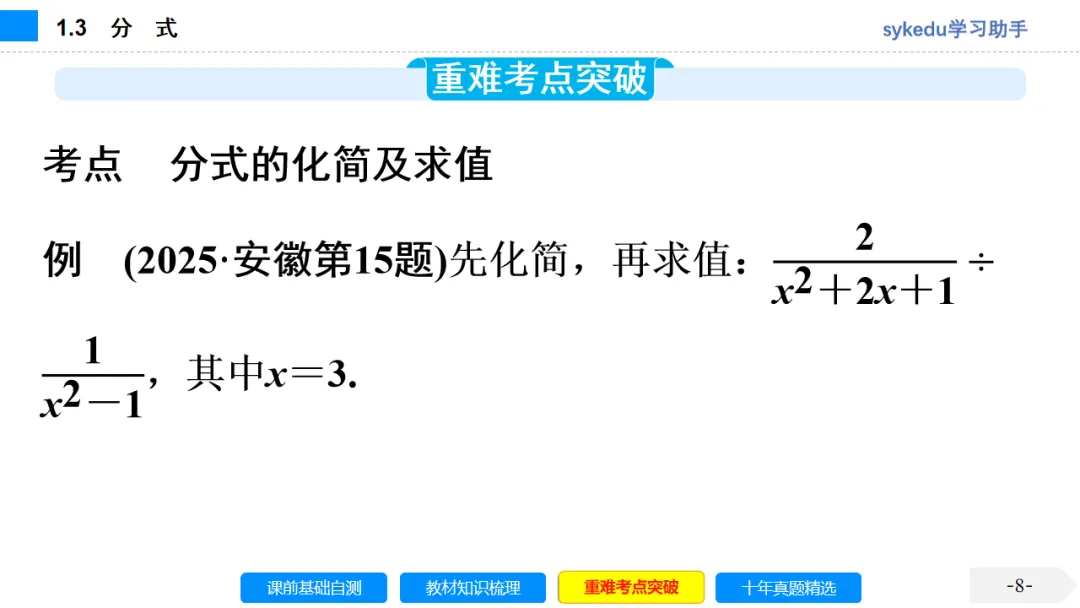
考点一        分　式

1．形如B(A)(A，B是整式，且B中含有字母)的式子叫做分式．

2．分式有无意义：当B＝0时，分式无意义；当B≠0时，分式有意义．

3．分式的值为0：当A＝0且B≠0时，分式的值为0.

温馨提示

B中含有字母是分式与分数概念的根本区别；判断一个式子是不是分式，若分子和分母含有公因式，不要约去公因式，直接根据概念判断即可.

考点二      分式的基本性质

1.b·m(a·m)＝b(a)，b÷m(a÷m)＝b(a)(m≠0)；

a(－b)＝－a(b)＝－a(b).

2．通分的关键是确定几个分式的最简公分母．确定最简公分母的一般步骤是：当分母是多项式时，先 因式分解，再取系数的最小公倍数与所有不同字母(因式)的最高次幂的积为最简公分母．

3．约分的关键是确定分式的分子与分母中的最大公因式．确定最大公因式的一般步骤是：当分子、分母是多项式时，先因式分解，再取系数的最大公约数　与相同字母(因式)的最低次幂的积为最大公因式．

温馨提示

1.若原分式的分子(或分母)是多项式，运用分式的基本性质时，要先把分式的分子(或分母)用括号括上，再乘(或除以)整式.

2.应用分式的基本性质时，要深刻理解“都”与“同”这两个字的含义，避免犯只乘分子或只乘分母的某一项的错误.

考点三       分式的运算

1．分式的加减法

同分母的分式相加减：c(a)±c(b)＝c(a±b)　；

异分母的分式相加减：b(a)±d(c)＝bd(ad±bc).

2．分式的乘除法

b(a)·d(c)＝bd(ac)　，b(a)÷d(c)＝b(a)·c(d)　＝bc(ad).

3．分式的乘方

(m(n))^k＝mk(nk)(m≠0，k是正整数)．

4．分式的混合运算

在分式的混合运算中，应先算乘方、开方，再算乘除，最后进行加减运算，如遇到有括号的，先算括号里面的．运算结果必须是最简分式或整式．

注意：在分式的运算中，分式只能通分，不能去分母．

考点四        分式求值

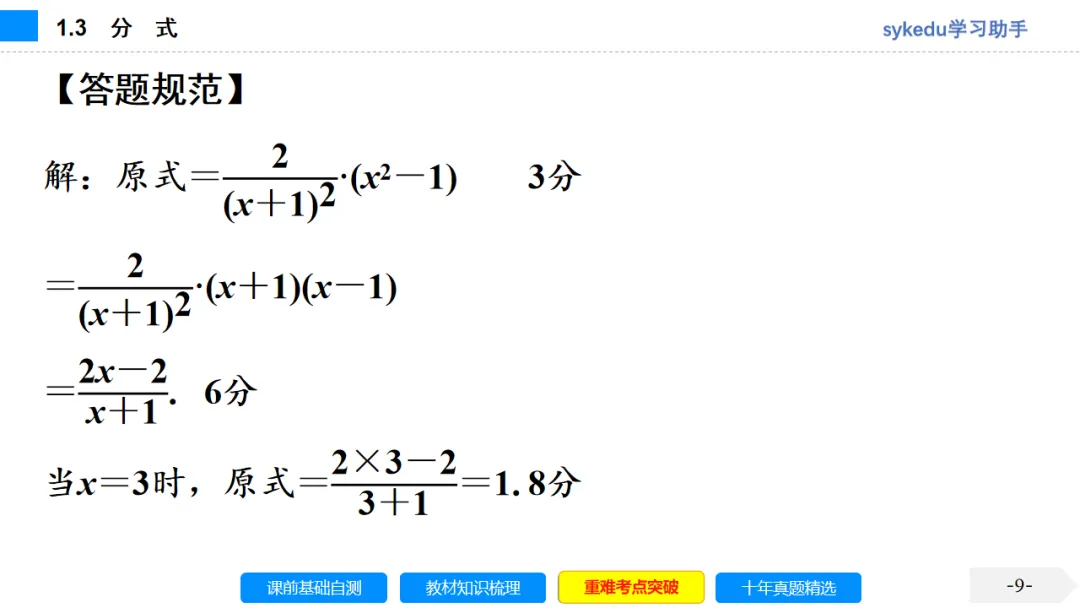
分式的求值方法很多，主要有三种：(1)先化简，再求值；(2)由值的形式直接转化成所求的代数式的值；(3)式中字母表示的数未明确告知，而是隐含在方程等题设条件中．解这类题，一方面从方程中求出未知数或未知代数式的值；另一方面把所求代数式适当地化简变形．两种方法同时用有时能获得简易的解法．

1.3　分　式-sykedu学习助手.pptx