
第(1)问思路1:
该抛物线的二次项系数已知,只剩下、两个待定系数 .将已知的点和代入即可列出关于、的二元一次方程组,解之即可得,.
第(1)问思路2:
由和两点的纵坐标相等,可知这两点关于该抛物线的对称轴对称,由此可得:
对称轴为直线:, 所以,
即,所以该抛物线的函数表达式为:,再将已知的点代一个进去,即可解得.
解决本问的关键是将,,,四个点求出(或表示)出来.
抛物线有三个待定系数,而已知其过,两点,虽不足以求出所有待定系数(需要已知三个点),但可以用其中一个系数表示另外两个系数 .这样,两点的坐标虽无法具体求出,但可以用同一个参数表示 .以上的理解是解题关键!
将和代入抛物线中,可得:
,,
所以抛物线的函数表达式可化为:
,
于是,
将该抛物线的函数表达式化为顶点式(或将代入),可求得:
,
这样,两点已经表示出来.又易求得:
和,
于是可得:,,
故.
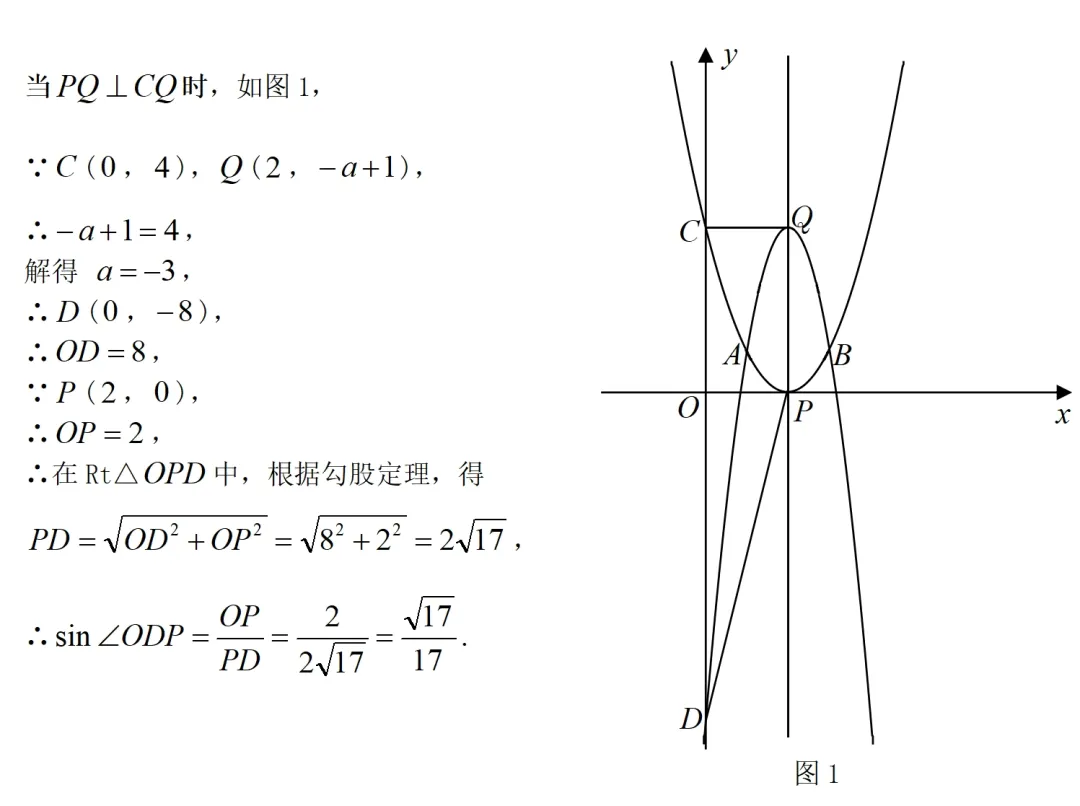
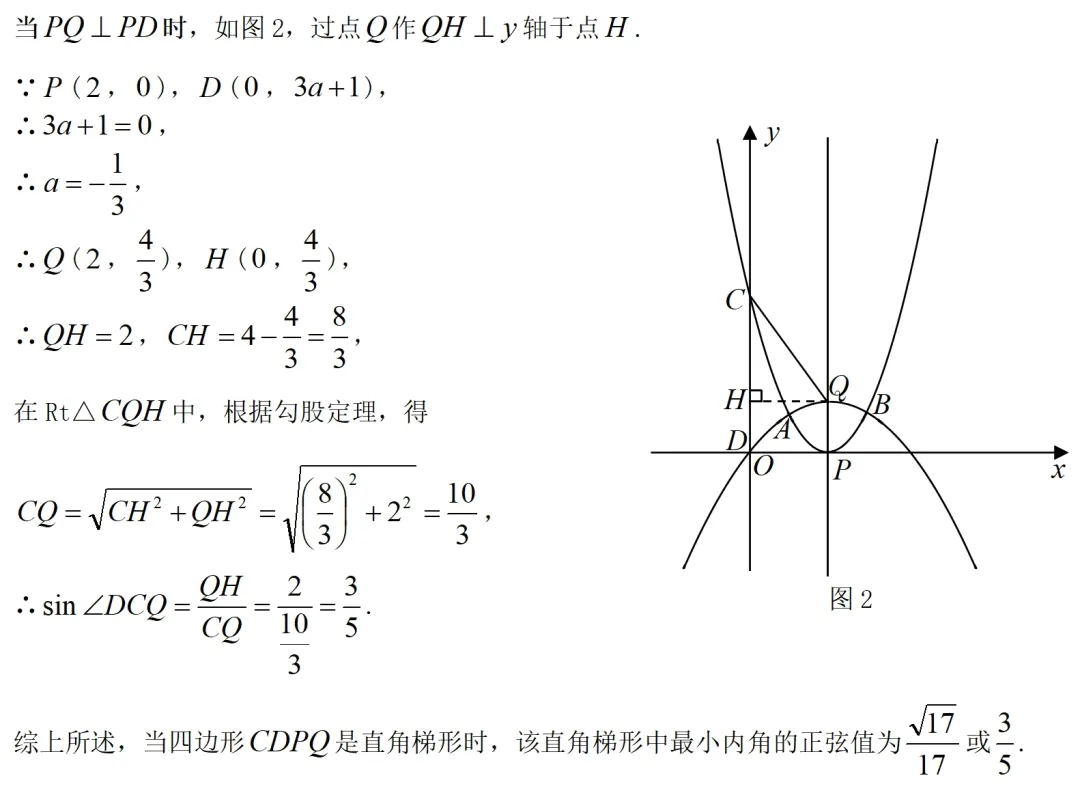
第(2)②问分析:
由于,两点在轴上,,两点在两条抛物线公共的对称轴上,故一定有.因此当四边形是直角梯形时,有和两种情况,需分类讨论 .熟练作图是解题关键!
文章来源:
四季读书网
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!





