
点
1.明确该点是定点还是动点;
2.确定点的具体坐标;
3.若涉及平移、旋转、轴对称、中心对称等几何变换,梳理该点与变换前/后对应点的关联;
4.判断点所在的图形(或运动轨迹);
5.若动点在圆上,需围绕圆心和半径展开分析。
直线/射线
1.区分是定直线还是动直线;
2.推导对应一次函数解析式(重点关注斜率k);
3.动直线的两类运动形式:绕定点旋转或平行平移;
4.若为绕定点旋转,留意“假对称真旋转”的特殊情况;
5.若存在几何变换(平移、旋转、轴对称、中心对称),分析变换前后直线的内在关系。
角
1.明确角的大小是否固定,尤其关注“定边对定角”(对应轨迹为圆弧)的情况;2确定角的位置(顶点位置、角的两边所在直线)是否固定;
3.若存在角平分线,可利用其自带的轴对称结构解题;
4.若角与圆相关,需判断其是否为圆心角或圆周角。
三角形
1.判断三角形是否为特殊三角形(369三角形、等边三角形、等腰直角三角形、普通等腰三角形、普通直角三角形);
2.部分特殊三角形(如等腰直角三角形、等边三角形)的顶点可通过旋转相互转化;3计算边长时,可结合勾股定理、相似三角形、三角函数三大传染工具进行转化求解。
平行四边形
1.抓住“对边平行且相等”的核心性质;
2.利用“对角线互相平分”的性质(可关联中心对称、8字全等、中点重合的两条线段);
3.以“以动制静”的视角分析平行四边形,其一条边可平移至对边位置。
矩形/正方形
1.沿用平行四边形的所有分析要点;
2.矩形的四个顶点都在以对角线为直径的圆上;
3.矩形可与直角三角形、等腰三角形相互转化解题。
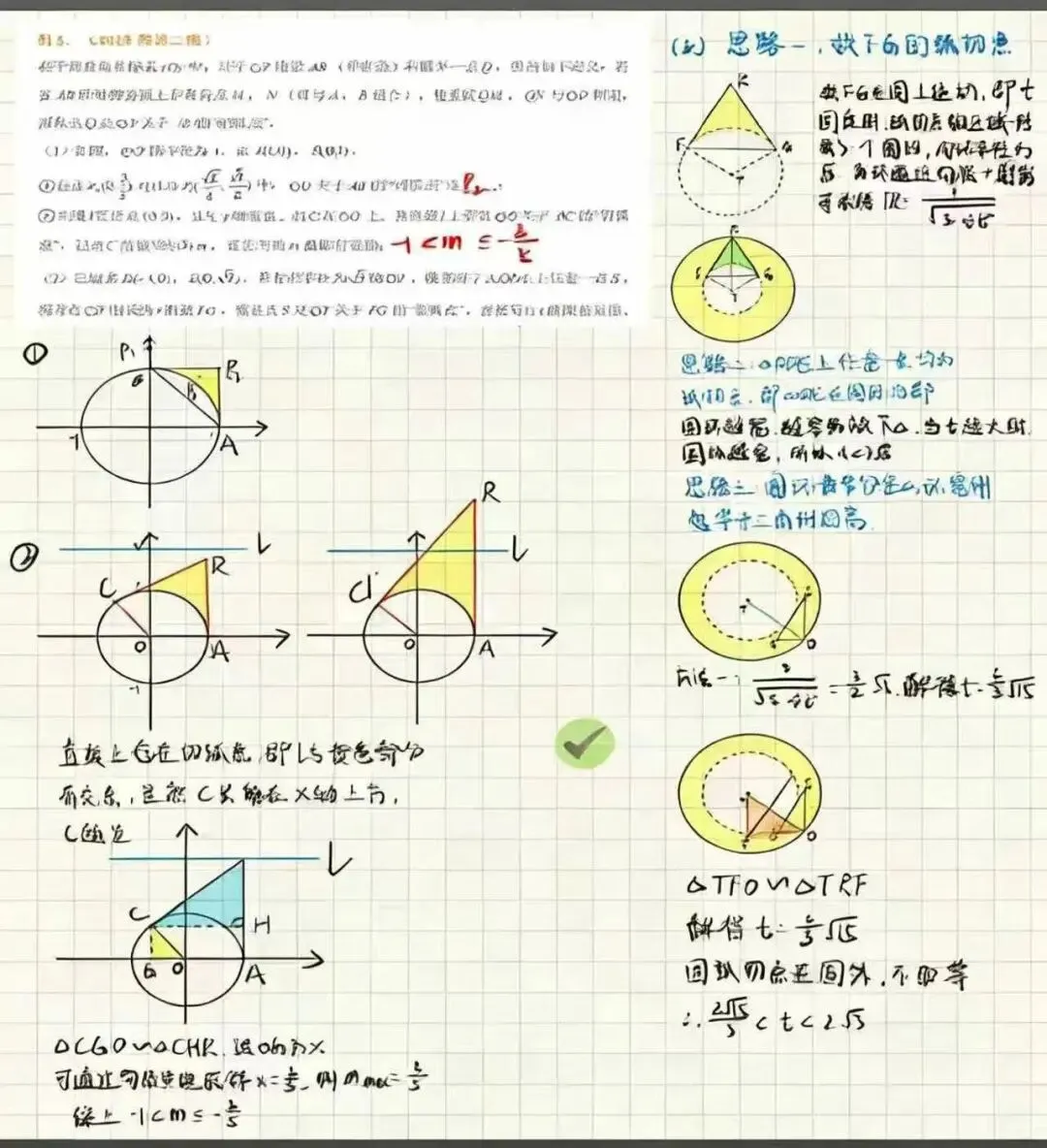
圆
1.决定性思维:圆心和半径是确定一个圆的两个关键元素;
2.明确点与圆的位置关系(圆内、圆上、圆外);
3.直线与圆相交时,优先联想垂径定理相关结构;
4.直线与圆相切时,重点寻找切线对应的直角三角形;
5.运用双节棍模型解题;
6掌握过圆内定点的最长弦(直径)和最短弦的相关规律。
圆弧
1.依据定义,遇到带“弧”的问题可先找垂足;
2.本质上仍是圆的一部分,核心仍是确定圆心和半径;
3.连接圆弧的两个端点可得到圆的弦,进而运用垂径定理相关结构。