n
专题03分式及分式方程
考点01 分式值为0或有意义
1．（2025·黑龙江齐齐哈尔·中考真题）若代数式有意义，则实数的取值范围是．
2．（2025·四川德阳·中考真题）函数y＝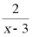
的自变量x的取值范围是．
3．（2024·黑龙江齐齐哈尔·中考真题）在函数中，自变量的取值范围是．
4．（2024·山东济南·中考真题）若分式的值为0，则的值是．
5．（2025·贵州·中考真题）若分式的值为0，则实数的值为（）
A．2B．0C．D．-3
6．（2023·四川凉山·中考真题）分式的值为0，则的值是（）
A．0B．C．1D．0或1
考点02 分式的化简计算
1．（2025·湖南·中考真题）约分：；
2．（2023·广东广州·中考真题）已知，代数式：，，．
(1)因式分解A；
(2)在A，B，C中任选两个代数式，分别作为分子、分母，组成一个分式，并化简该分式．
3．（2025·黑龙江绥化·中考真题）计算：．
4．（2025·陕西·中考真题）化简：．
5．（2025·江西·中考真题）化简：
6．（2024·甘肃临夏·中考真题）化简：．
7．（2023·陕西·中考真题）化简：．
8．（2023·湖南常德·中考真题）先化简，再求值：，其中．
考点03 分式化简求值
1．（2025·北京·中考真题）已知，求代数式的值．
2．（2025·青海·中考真题）先化简，再从，，中选一个合适的数代入求值．
3．（2025·黑龙江·中考真题）先化简，再求值：，其中．
4．（2025·吉林·中考真题）先化简，再求值：，其中．
5．（2025·重庆·中考真题）先化简，再求值：，其中．
6．（2024·广东深圳·中考真题）先化简，再代入求值：，其中．
7．（2024·西藏·中考真题）先化简，再求值：，请为m选择一个合适的数代入求值．
8．（2024·山东淄博·中考真题）化简分式：，并求值（请从小宇和小丽的对话中确定，的值）
9．（2023·湖北鄂州·中考真题）若实数、分别满足，，且，则．
10．（2023·青海西宁·中考真题）先化简，再求值：，其中，是方程的两个根．
考点04 解分式方程
1．（2025·北京·中考真题）方程的解为．
2．（2025·湖南长沙·中考真题）分式方程的解为．
3．（2024·青海西宁·中考真题）解方程：．
4．（2024·山东济宁·中考真题）解分式方程时，去分母变形正确的是（）
A．B．
C．D．
5．（2017·四川绵阳·中考真题）关于x的分式方程的解是．
6．（2025·上海·中考真题）解方程：．
7．（2025·黑龙江·中考真题）已知关于的分式方程解为负数，则的值为（）
A．B．C．且D．且
8．（2025·黑龙江齐齐哈尔·中考真题）如果关于的分式方程无解，那么实数的值是（）
A．B．C．或D．且
9．（2025·四川眉山·中考真题）若关于x的不等式组至少有两个正整数解，且关于x的分式方程的解为正整数，则所有满足条件的整数a的值之和为（）
A．8B．14C．18D．38
10．（2024·重庆·中考真题）若关于的不等式组至少有2个整数解，且关于的分式方程的解为非负整数，则所有满足条件的整数的值之和为．
11．（2023·湖南永州·中考真题）若关于x的分式方程（m为常数）有增根，则增根是．
考点05 分式方程的实际应用
1．（2025·吉林长春·中考真题）小吉和小林从同一地点出发跑800米，小吉的平均速度是小林的1.25倍，结果小吉比小林少用40秒到达终点．求小林跑步的平均速度．
2．（2024·黑龙江绥化·中考真题）一艘货轮在静水中的航速为，它以该航速沿江顺流航行所用时间，与以该航速沿江逆流航行所用时间相等，则江水的流速为（）
A．B．C．D．
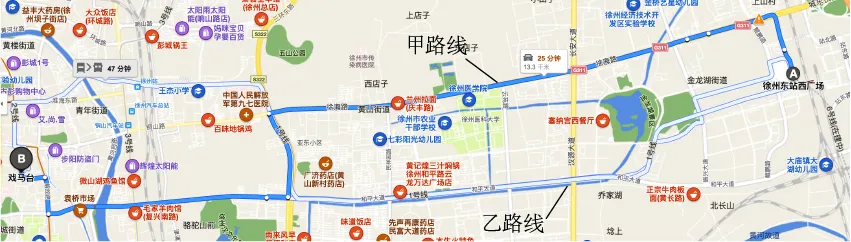
3．（2023·江苏徐州·中考真题）随着2022年底城东快速路的全线通车，徐州主城区与东区之间的交通得以有效改善，如图某人乘车从徐州东站至戏马台景区，可沿甲路线或乙路线前往．已知甲、乙两条路线的长度均为，甲路线的平均速度为乙路线的倍，甲路线的行驶时间比乙路线少，求甲路线的行驶时间．
4．（2025·山西·中考真题）我国自主研发的型快速换轨车，采用先进的自动化技术、能精准高效地完成更换铁路钢轨的任务．一辆该型号快速换轨车每小时更换钢轨的公里数是一个工作队人工更换钢轨的2倍，它更换116公里钢轨比一个工作队人工更换80公里钢轨所用时间少22小时．求一辆该型号快速换轨车每小时更换钢轨多少公里．
5．（2025·黑龙江绥化·中考真题）用A，两种货车运输化工原料，A货车比货车每小时多运输15吨，A货车运输450吨所用时间与货车运输300吨所用时间相等．若设货车每小时运输化工原料吨，则可列方程为（）
A．B．C．D．
6．（2024·四川达州·中考真题）甲乙两人各自加工120个零件，甲由于个人原因没有和乙同时进行，乙先加工30分钟后，甲开始加工．甲为了追赶上乙的进度，加工的速度是乙的倍，最后两人同时完成．求乙每小时加工零件多少个？设乙每小时加工个零件．可列方程为（）
A．B．
C．D．
7．（2023·辽宁丹东·中考真题）“畅通交通，扮靓城市”，某市在道路提升改造中，将一座长度为36米的桥梁进行重新改造．为了尽快通车，某施工队在实际施工时，每天工作效率比原计划提高了，结果提前2天成功地完成了大桥的改造任务，那么该施工队原计划每天改造多少米?
8．（2025·江苏扬州·中考真题）某文创商店推出甲、乙两款具有纪念意义和实用价值的书签，已知甲款书签价格是乙款
通过网盘分享的文件：三年（2023-2025）中考真题分类汇编（全国通用）
链接: https://pan.baidu.com/s/1489j7ii8Wz9ALgJ8AqGKCg?pwd=4321 提取码: 4321
--来自百度网盘超级会员v8的分享
