中考数学二次函数:这些＂套路＂学会了,压轴题不再怕

说起二次函数，很多同学都觉得这是中考数学的一座大山。抛物线画来画去，动点移来移去，最后把自己绕晕了。其实啊，二次函数的题目虽然变化多端，但核心规律就那么几条，掌握了这些"套路"，你会发现这类题目其实很有规律可循。

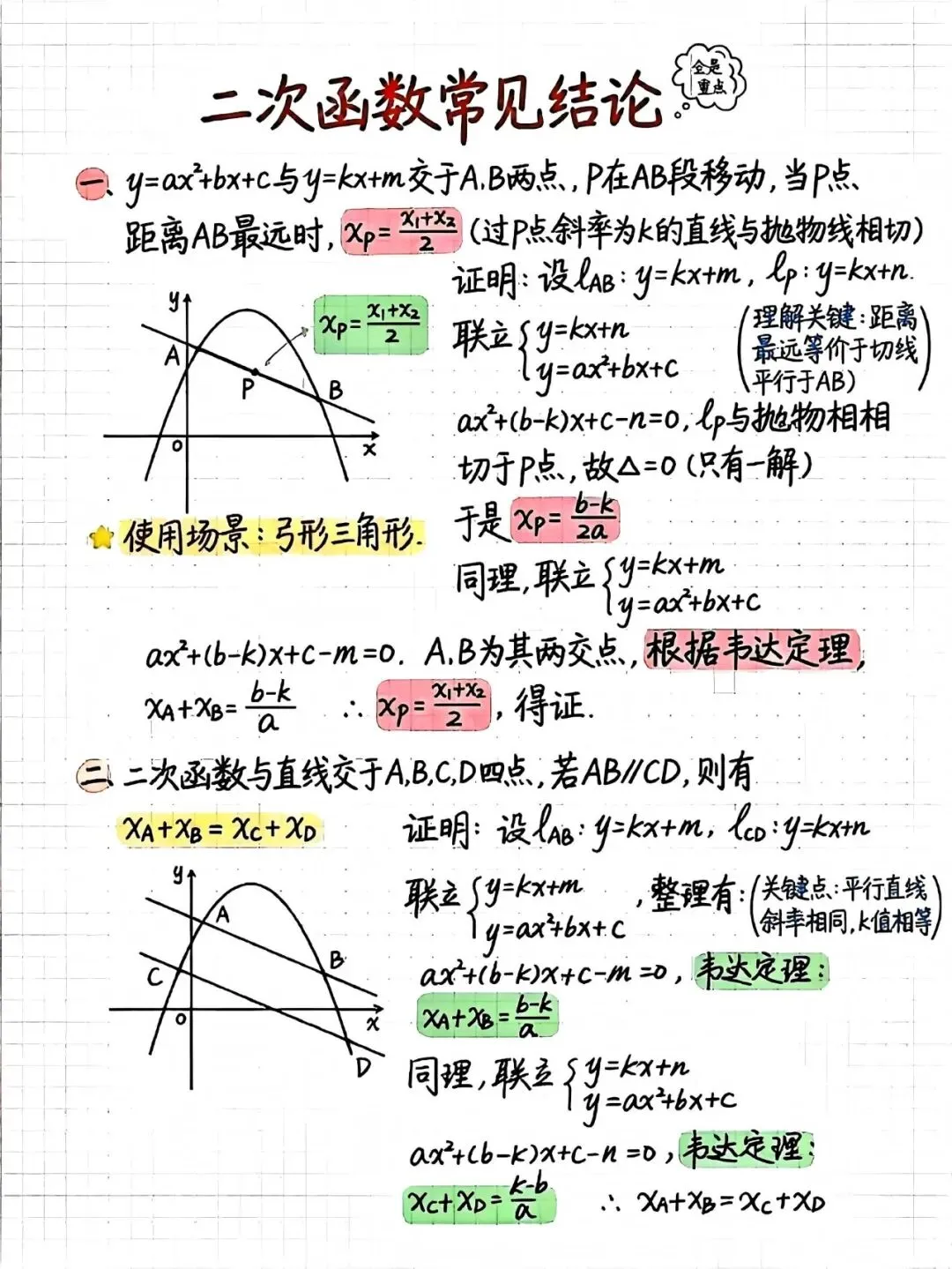
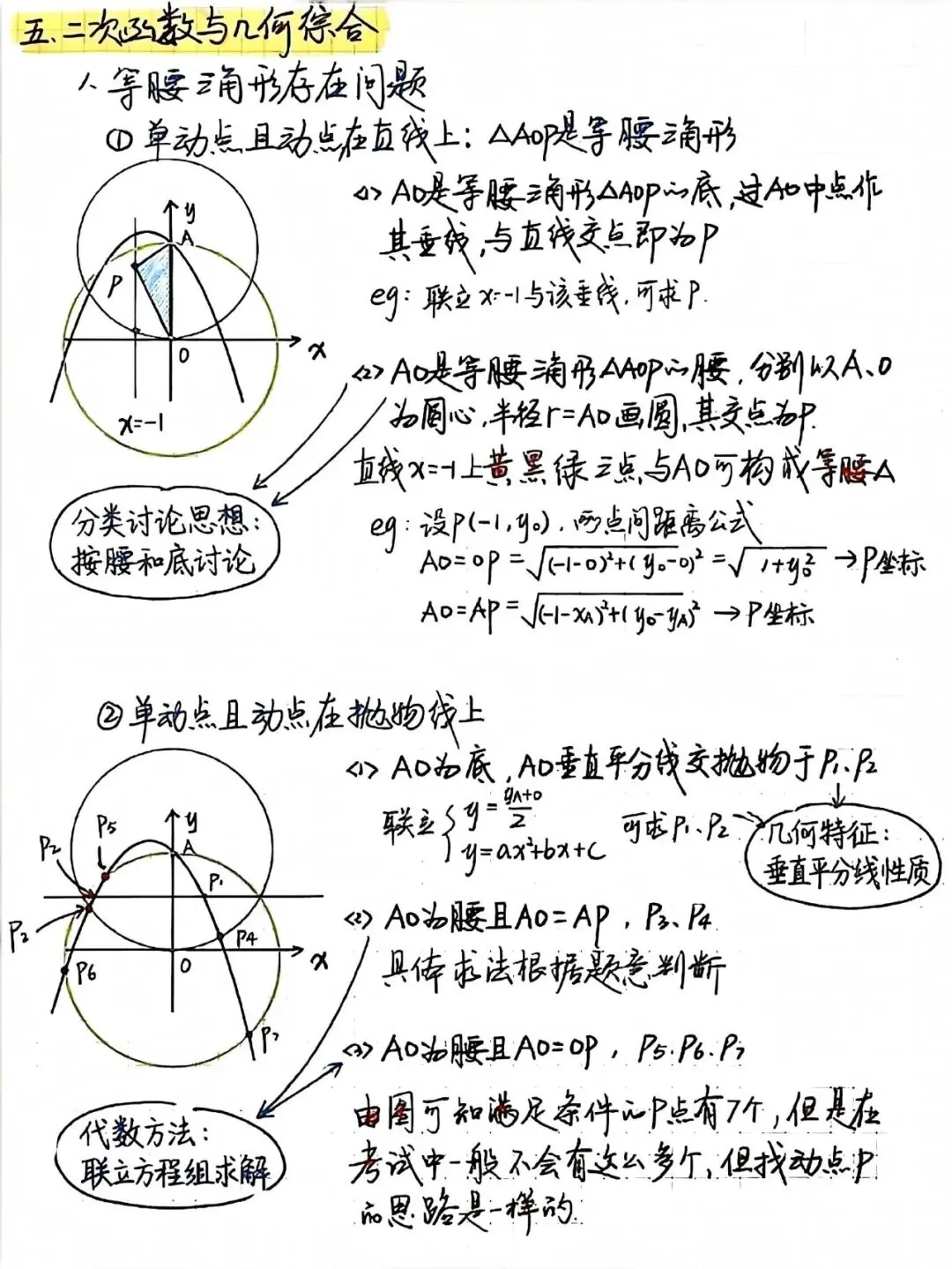
先说说最基础的。当你看到一条抛物线和一条直线相交于A、B两点，题目问抛物线上哪一点P到直线AB的距离最远时，很多同学会想着用点到直线的距离公式硬算，结果算得满头大汗。其实有个巧妙的方法：距离最远的时候，过P点且平行于AB的直线刚好与抛物线相切。这时候P点的横坐标正好是A、B两点横坐标的平均值，也就是中点。这个结论记下来，遇到"弓形三角形"面积最大的问题直接就能用，省去了复杂的计算过程。

再来说说平行线的性质。如果两条平行线分别与抛物线相交，得到A、B和C、D四个交点，那么有个有趣的规律：A和B的横坐标之和，等于C和D的横坐标之和。这个结论看起来简单，但在解决一些对称性问题时特别好用。背后的原理其实不难理解，因为平行线的斜率相同，联立方程后，根据韦达定理，一次项系数的比值是一样的，所以横坐标之和也相等。

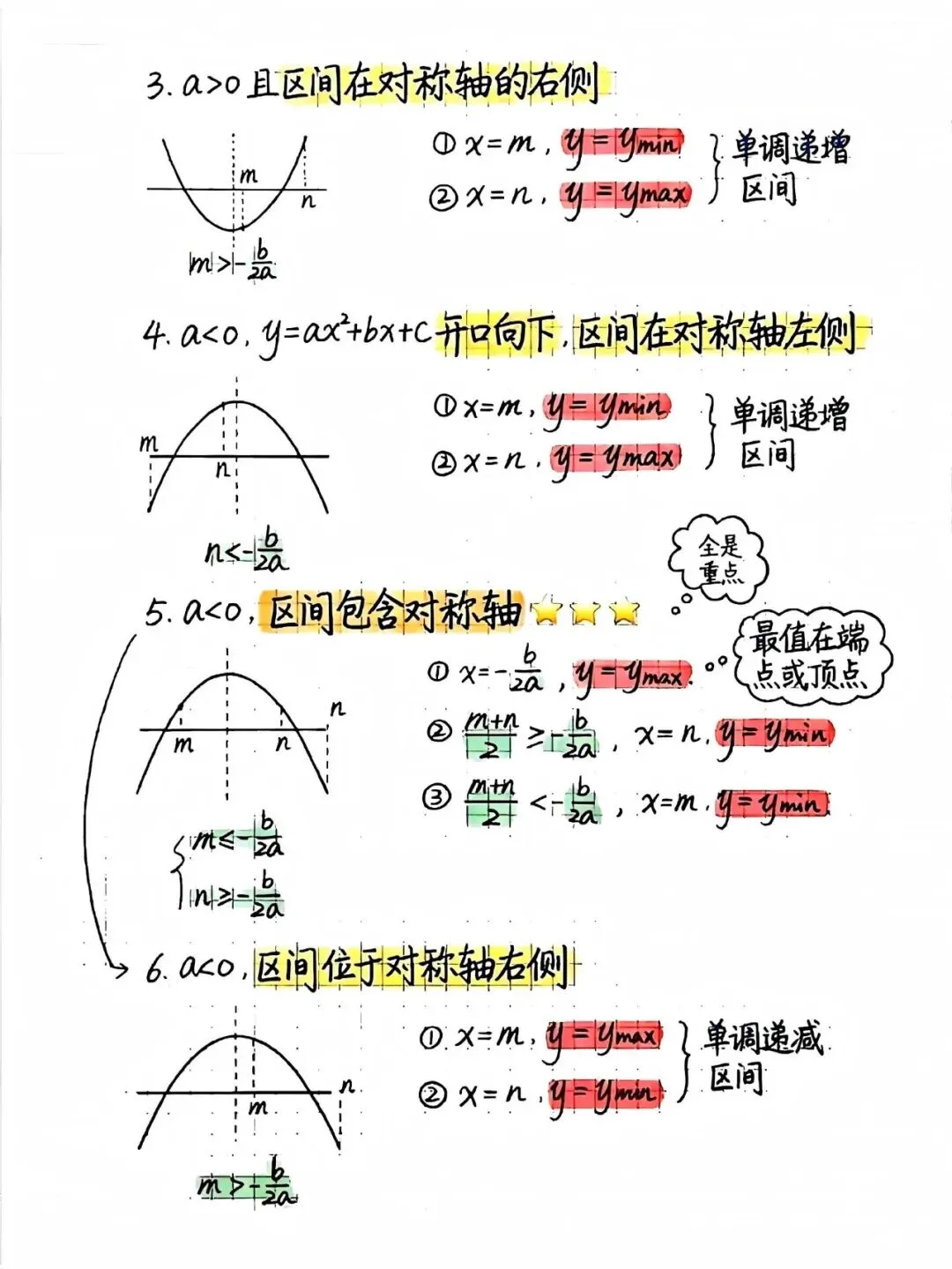
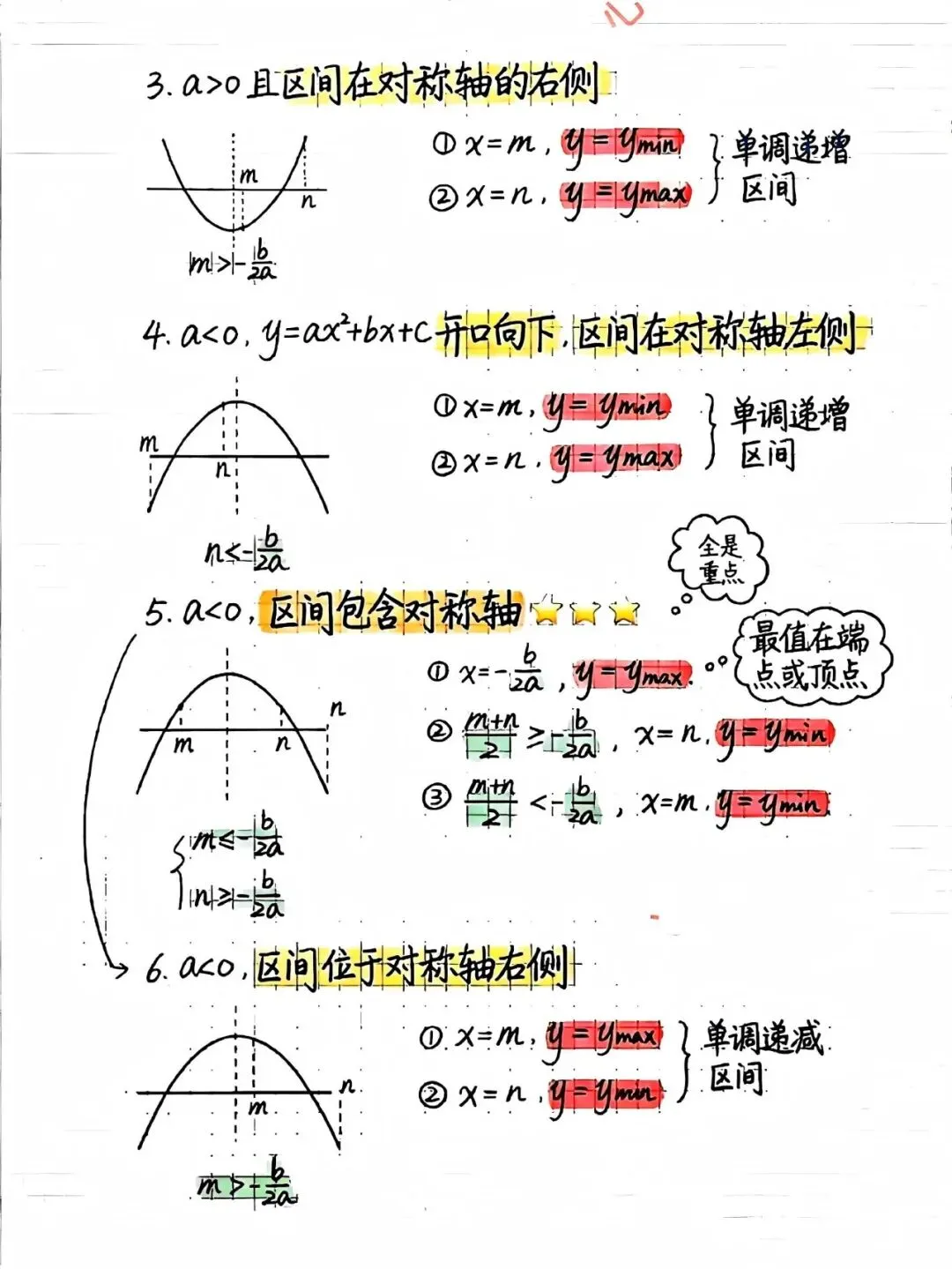
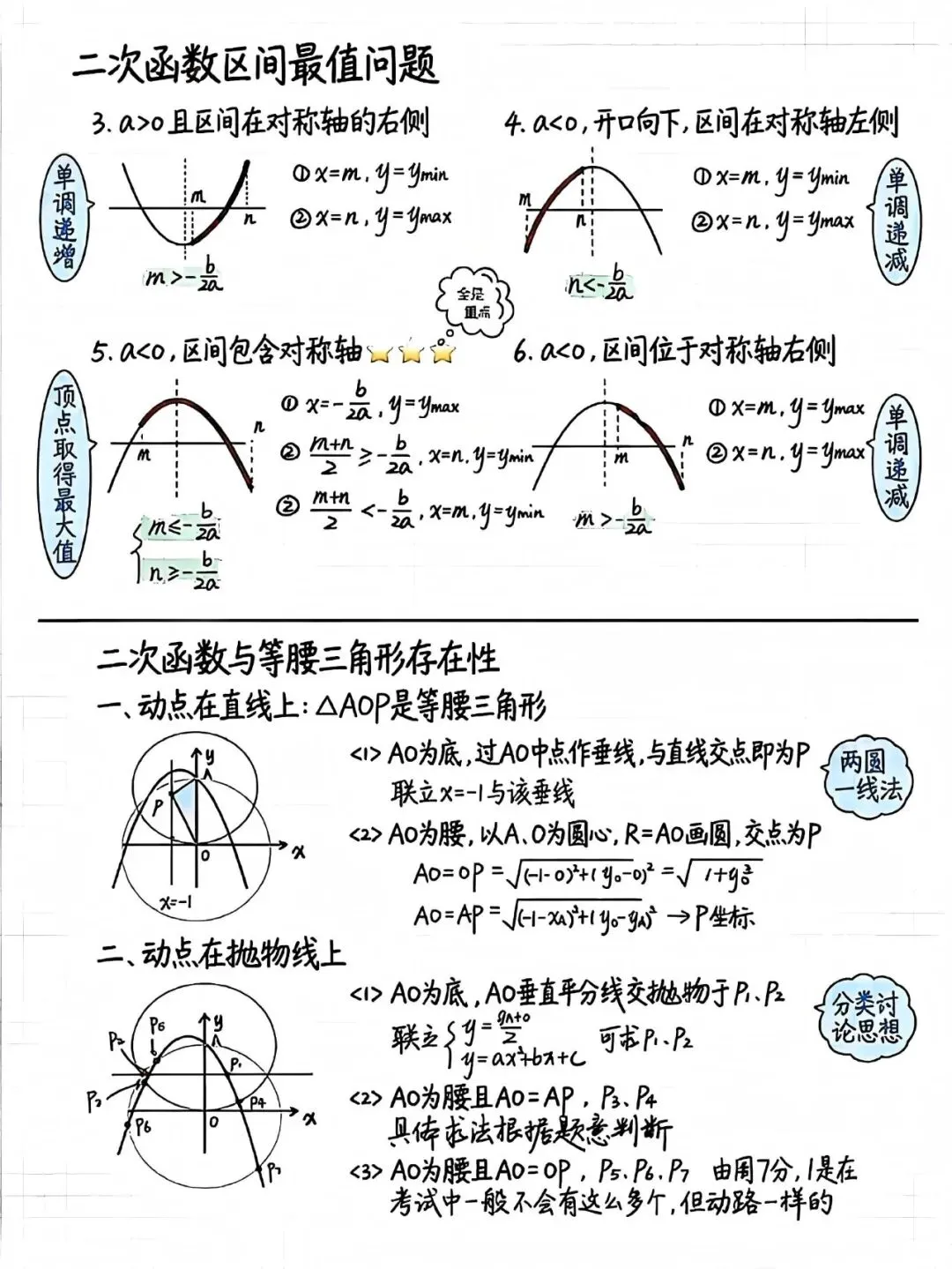
区间最值问题是很多同学的老大难。其实判断方法很直观：如果抛物线开口向上，对称轴在区间左边，那么区间内函数单调递增，最小值在左端点，最大值在右端点；如果对称轴在区间右边，情况正好相反。最复杂的是对称轴落在区间内的情况，这时候要先看区间中点和对称轴的位置关系。如果中点在对称轴右边，说明右端点离对称轴更远，最大值就在右端点；反之则在左端点。记住这个规律，分类讨论时就不会漏情况。

下面分享二次函数常见结论，一定要熟练掌握。