一、什么叫“隐形圆”?
隐形圆不是题目直接画出来的圆,而是:
题中出现了圆的关键条件
但圆没有明确给出
需要你自己“补出圆”“想到圆”
一句话:
看到某些几何特征,就要想到背后可能藏着一个圆。
二、中考隐形圆的4大核心考点
考点1:看到“等角” → 想到“同弧所对的圆”
典型信号
∠ABC = ∠ADC
两个角截同一条线段
结论
四点共圆
即:
A、B、C、D 在同一个圆上
中考常用一句话
同弧所对的圆周角相等 → 四点共圆
例题套路
若:
∠BAC = ∠BDC则:
A、B、C、D 共圆
考点2:看到“直角” → 想到“直径所对圆周角”
典型信号
∠ABC = 90°
有“垂直”关系
结论
直角对应的两点是直径端点
即:
A、C 是圆的直径
中考公式
圆周角是90° → 对应弦是直径
隐形圆最经典模型
若:
∠ABC = 90°则:
A、B、C 在同一圆上,AC 为直径
考点3:看到“等长” → 想到“圆的半径”
典型信号
OA = OB
PA = PB
两条线段相等
结论
以某点为圆心的圆出现了
例如:
OA = OB说明:
A、B 在以 O 为圆心的圆上
常见隐形圆模型
若:
PA = PB则:
P 在 AB 的垂直平分线上→ 可构造圆
考点4:看到“切线” → 想到“切线性质”
典型信号
“切于某点”
“切线”
“⊥ 半径”
结论
切点处半径垂直切线
公式:
OT ⟂ 切线
中考最爱考
切线角定理
切线长定理
三、隐形圆的万能识别口诀
一眼识圆口诀(中考最实用)
见直角想直径见等角想共圆见等长想半径见切线想垂直
四、隐形圆题型的3大解题套路
套路1:补圆(构造圆)
题目不给圆 → 自己画出来
方法
找直径端点
找圆心(垂直平分线交点)
找共圆四点
套路2:证四点共圆(中考必考)
最常用判定方法
最常用一句话模板
因为∠ABC = ∠ADC所以四点 A、B、C、D 共圆。
套路3:用圆的性质秒杀角度与长度
一旦补出圆,就立刻用:
圆的三大核心性质
同弧所对圆周角相等
直径所对圆周角是90°
切线 ⟂ 半径
五、中考隐形圆常见压轴结构
结构1:直角三角形 + 隐形圆
90° → 直径
常用于最值、证明
结构2:四边形共圆 + 角度转换
等角 → 共圆
常用于角追
结构3:切线 + 圆周角
切线角定理
常用于证明角相等
六、隐形圆题的得分策略(考场必用)
第一步:圈关键词
90°
相等角
切线
等长
第二步:写“共圆”结论
能共圆就立刻写:
四点共圆
第三步:马上调用圆性质
同弧等角
直径直角
切线垂直
七、隐形圆万能答题模板(直接套)
模板1:证四点共圆
因为∠ABC = ∠ADC所以点A、B、C、D在同一圆上。
模板2:直角推出直径
因为∠ABC = 90°所以AC为圆的直径。
模板3:切线性质
因为PT是圆的切线所以OT ⟂ PT。
八、总结:隐形圆=中考几何的“隐藏钥匙”
隐形圆题的核心不是难,而是:
你能不能第一眼看出圆藏在哪里。
中考隐形圆最重要能力:
识圆
补圆
用圆解题
一
四点共圆
【二动点到定点等于定长】

【三直角所对的是直径】

【四定弦对定角】

【一定角定高】

二
定角定周
“定角定周”三角形的三种处理手段
1 、转化为“定弦定角”
延长CB 至D,使得BD=AB,延长BC至E,使得CE=AC,则DE的长等于△ABC 的周长,
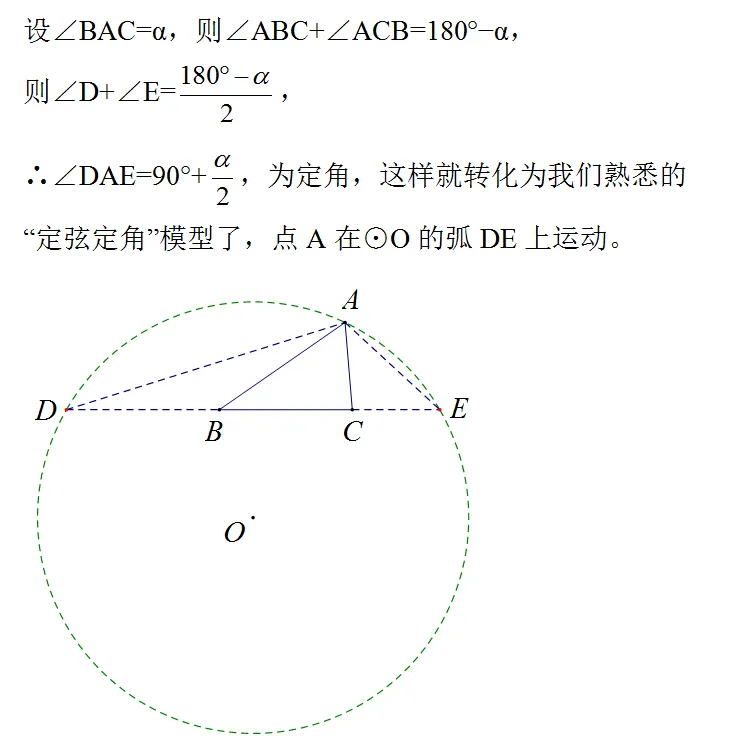
2 、转化为“定角定高”
作△ABC 的旁切圆⊙O ,则△ODB≌△OEB ,△ODC≌△OFC,∴BD=BE,CD=CF,∴AE+AF等于△ABC 的周长,又∵△AOE≌△AOF ,∴AE=AF ,为定值。
∵∠BAC 为定角,∴∠OAF=∠OAE ,为定角,∴OD=OE=OF ,为定值,
三
定角定中线
【模型解读】
如图,在△ABC中,∠BAC的大小是定值,中线AD的长为定值,满足以上条件的三角形称为“定角定中线”三角形。这类模型其实是“定弦定角”隐形圆的变形,解决办法是通过倍长中线法,将其转化为我们更熟悉的“定弦定角”模型。
四
定角定平分线
【模型解读】
如图,已知△ABC 中,∠BAC=α (定角),AD平分∠BAC ,且AD=m(定值),我们把这类三角形称为“定角定角平分线模型”,下面我们来研究一下它可能会考查哪些问题。