2025年云南省中考数学试卷
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2分)中国是最早使用正负数表示具有相反意义的量的国家.若收入10元记作+10元,则支出5元可记作( )
A.﹣5元B.5元C.﹣10元D.10元
2.(2分)地球绕太阳公转的速度约是110000km/h.110000用科学记数法可以表示为( )
A.1.1×102B.11×103C.1.1×105D.11×107
3.(2分)如图,已知直线c与直线a,b都相交.若a∥b,∠1=50°,则∠2=( )
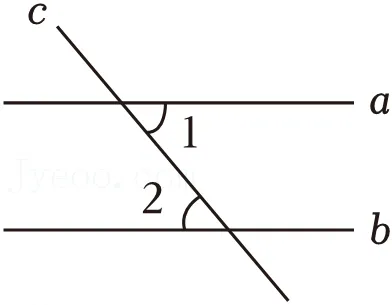
A.53°B.52°C.51°D.50°
4.(2分)下列计算正确的是( )
A.x+2x=3x2B.x2•x3=x5C.x6÷x2=xD.(xy)2=xy2
5.(2分)若点(1,2)在反比例函数y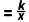 (k为常数,且k≠0)的图象上,则k=( )
(k为常数,且k≠0)的图象上,则k=( )
A.1B.2C.3D.4
6.(2分)下列图形是某几何体的三视图(主视图也称正视图,左视图也称侧视图),则这个几何体是( )
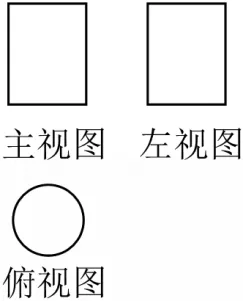
A.正方体B.长方体C.圆锥D.圆柱
7.(2分)一个六边形的内角和等于( )
A.360°B.540°C.720°D.900°
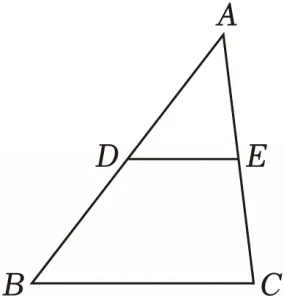
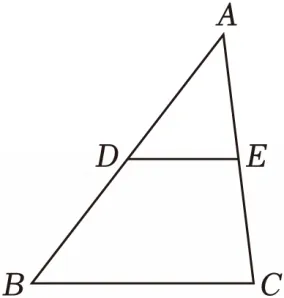
8.(2分)如图,在△ABC中,已知D,E分别是AB,AC边上的点,且DE∥BC.若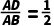 ,则
,则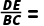 ( )
( )
A.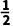 B.
B.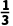 C.
C.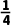 D.
D.
9.(2分)函数y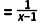 的自变量x的取值范围为( )
的自变量x的取值范围为( )
A.x≠4B.x≠3C.x≠2D.x≠1
10.(2分)中华文明,源远流长;中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )
A.B.C.D.
11.(2分)某校举办了关于垃圾分类的知识竞赛.九年级10名学生参加本次竞赛的成绩(单位:分)分别为90,80,90,70,90,100,80,90,90,80.这组数据的众数是( )
A.70B.80C.90D.100
12.(2分)按一定规律排列的代数式:a,3a,5a,7a,9a,⋯,第n个代数式是( )
A.(2n﹣1)aB.(2n+1)aC.(n+1)aD.2025a
13.(2分)若一个圆锥的侧面展开图的圆心角度数为90°,母线长为40cm,则该圆锥的底面圆的半径为( )
A.9cmB.10cmC.11cmD.12cm
14.(2分)某书店今年3月份盈利6000元,5月份盈利6200元.设该书店每月盈利的平均增长率为x.根据题意,下列方程正确的是( )
A.6000(1+x)2=6200B.6000(1﹣x)2=6200
C.6000(1+2x)=6200D.6000x2=6200
15.(2分)如图,在Rt△ABC中,∠C=90°.若AB=13,BC=5,则sinA=( )
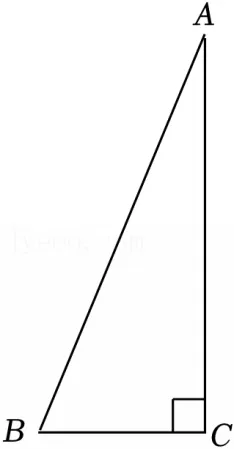
A. B.
B.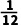 C.
C.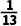 D.
D.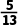
二、填空题:本题共4小题,每小题2分,共8分。
16.(2分)已知⊙O的半径为5cm.若点P在⊙O上,则点P到圆心O的距离为cm.
17.(2分)分解因式:x2+x= .
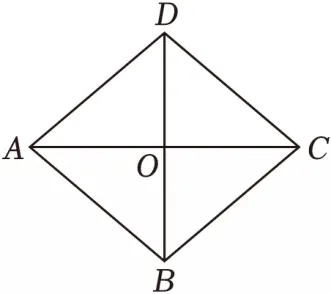
18.(2分)如图,四边形ABCD是菱形,对角线AC,BD相交于点O.若AC=6,BD=5,则菱形ABCD的面积是 .
19.(2分)某中学为了解全校1000名学生对新闻,娱乐,体育,动画,戏曲五类电视节目的喜爱情况,学校就“我最喜爱的电视节目”作了一次简单随机抽样调查.如图是根据调查结果绘制的扇形统计图.根据图中的信息,该校1000名学生中,最喜爱娱乐节目的学生大约有 名.

三、解答题:本题共8小题,共62分。解答应写出文字说明、证明过程或演算步骤。
20.(7分)计算:(π﹣2)0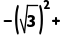 |﹣6|
|﹣6|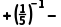 2cos60°.
2cos60°.
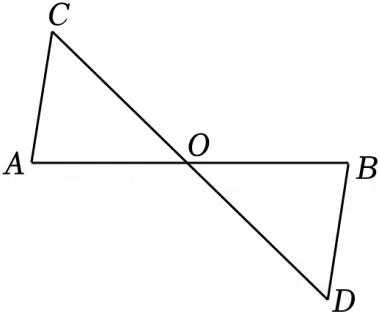
21.(6分)如图,AB与CD相交于点O,AC=BD,∠C=∠D.
求证:△AOC≌△BOD.
22.(7分)某化工厂采用机器人A,机器人B搬运化工原料,机器人A比机器人B每小时少搬运20千克,机器人A搬运800千克所用时间与机器人B搬运1000千克所用时间相等.求机器人A,机器人B每小时分别搬运多少千克化工原料.
23.(6分)九年级某班学生计划到甲,乙两个敬老院开展献爱心活动,老师把该班学生分成A,B两个小组,通过游戏方式确定去哪个敬老院.
游戏规则如下:在一个不透明的箱子中放了分别标有数字1,2的两张卡片(除数字外,都相同),班长先从这个箱子里任意摸出一张卡片,卡片上的数字记为x.在另一个不透明的箱子中放了分别标有数字1,2,3的三张卡片(除数字外,都相同),班长再从该箱子里任意摸出一张卡片,卡片上的数字记为y.若x=y,则A组学生到甲敬老院,B组学生到乙敬老院;若x≠y,则A组学生到乙敬老院,B组学生到甲敬老院.
(1)用列表法或画树状图法中的一种方法,求(x,y)所有可能出现的结果总数;
(2)求A组学生到甲敬老院,B组学生到乙敬老院开展献爱心活动的概率P.
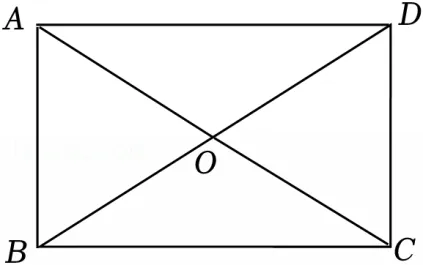
24.(8分)如图,在△ABC中,∠ABC=90°,O是AC的中点.延长BO至点D,使OD=OB.连接AD,CD.记AB=a,BC=b,△AOB的周长为l1,△BOC的周长为l2,四边形ABCD的周长为l3.
(1)求证:四边形ABCD是矩形;
(2)若l2﹣l1=2,l3=28,求AC的长.
25.(8分)请你根据下列素材,完成有关任务.
背景 | 某校计划购买篮球和排球,供更多学生参加体育锻炼,增强身体素质. |
素材一 | 购买2个篮球与购买3个排球需要的费用相等; |
素材二 | 购买2个篮球和5个排球共需800元; |
素材三 | 该校计划购买篮球和排球共60个,篮球和排球均需购买,且购买排球的个数不超过购买篮球个数的2倍. |
请完成下列任务: | |
任务一 | 每个篮球,每个排球的价格分别是多少元? |
任务二 | 给出最节省费用的购买方案. |
26.(8分)已知a是常数,函数y=(x+4)(x﹣a2+a﹣3)+1,记T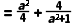 .
.
(1)若x=﹣4,a=1,求y的值;
(2)若x=3a+2,y=1,比较T与3的大小.
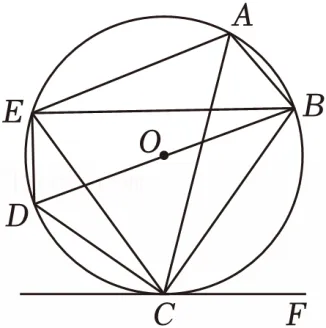
27.(12分)如图,⊙O是五边形ABCDE的外接圆,BD是⊙O的直径.连接AC,BE,CE,∠AEC=∠ACF.
(1)若CE=CB,且∠CBE=60°,求∠BCE的度数;
(2)求证:直线CF是⊙O的切线;
(3)探究,发现与证明:
已知AC平分∠BAE,是否存在常数a,b,使等式AC2=aBC•CE+bAB•AE成立?若存在,请直接写出一个a的值和一个b的值,并证明你写出的a的值和b的值,使等式AC2=aBC•CE+bAB•AE成立;若不存在,请说明理由.
2025年云南省中考数学试卷
参考答案与试题解析
一.选择题(共15小题)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
答案 | A. | C. | D | B | B | D | C | A | D | C | C |
题号 | 12 | 13 | 14 | 15 | |||||||
答案 | A | B | A | D | |||||||
一、选择题:本题共15小题,每小题2分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.【2025·云南】中国是最早使用正负数表示具有相反意义的量的国家.若收入10元记作+10元,则支出5元可记作( )
A.﹣5元B.5元C.﹣10元D.10元
【答案】A
2.【2025·云南】地球绕太阳公转的速度约是110000km/h.110000用科学记数法可以表示为( )
A.1.1×102B.11×103C.1.1×105D.11×107
【答案】C
3.【2025·云南】如图,已知直线c与直线a,b都相交.若a∥b,∠1=50°,则∠2=( )
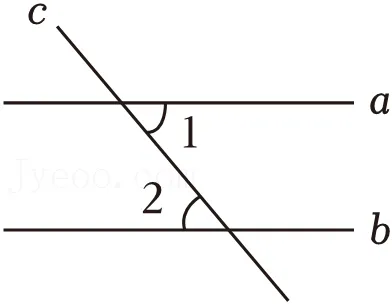
A.53°B.52°C.51°D.50°
【答案】D
4.【2025·云南】下列计算正确的是( )
A.x+2x=3x2B.x2•x3=x5C.x6÷x2=xD.(xy)2=xy2
【答案】B
5.【2025·云南】若点(1,2)在反比例函数y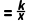 (k为常数,且k≠0)的图象上,则k=( )
(k为常数,且k≠0)的图象上,则k=( )
A.1B.2C.3D.4
【答案】B【解析】把点(1,2)代入反比例函数y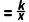 (k为常数,且k≠0)中,得2
(k为常数,且k≠0)中,得2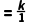 ,解得k=2.
,解得k=2.
6.【2025·云南】下列图形是某几何体的三视图(主视图也称正视图,左视图也称侧视图),则这个几何体是( )
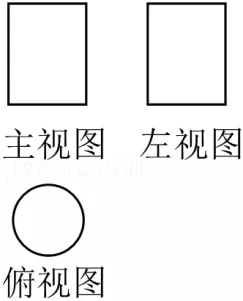
A.正方体B.长方体C.圆锥D.圆柱
【答案】D【解析】根据主视图和左视图为矩形可判断出是柱体,根据俯视图是圆形可判断出这个几何体是圆柱.
7.【2025·云南】一个六边形的内角和等于( )
A.360°B.540°C.720°D.900°
【答案】C【解析】一个六边形的内角和等于(6﹣2)×180°=720°.
8.【2025·云南】如图,在△ABC中,已知D,E分别是AB,AC边上的点,且DE∥BC.若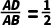 ,则
,则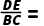 ( )
( )
A.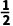 B.
B.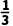 C.
C.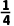 D.
D.
【答案】A【解析】∵DE∥BC,∴△ADE∽△ABC,∴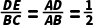 .
.
9.【2025·云南】函数y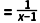 的自变量x的取值范围为( )
的自变量x的取值范围为( )
A.x≠4B.x≠3C.x≠2D.x≠1
【答案】D【解析】已知函数y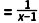 ,则x﹣1≠0,即x≠1.
,则x﹣1≠0,即x≠1.
10.【2025·云南】中华文明,源远流长;中华汉字,寓意深广.下列四个选项中,是轴对称图形的为( )

【答案】C【解析】A,B,D选项中的汉字都不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;C选项中的汉字能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形.
11.【2025·云南】某校举办了关于垃圾分类的知识竞赛.九年级10名学生参加本次竞赛的成绩(单位:分)分别为90,80,90,70,90,100,80,90,90,80.这组数据的众数是( )
A.70B.80C.90D.100
【答案】C【解析】在这一组数据中90是出现次数最多的,故众数是90.
12.【2025·云南】按一定规律排列的代数式:a,3a,5a,7a,9a,⋯,第n个代数式是( )
A.(2n﹣1)aB.(2n+1)aC.(n+1)aD.2025a
【答案】A【解析】第1个代数式为a,第2个代数式为3a,第3个代数式为5a,第4个代数式为7a,第5个代数式为9a,…,以此类推,可知,第n个代数式是 (2n﹣1)a.
13.【2025·云南】若一个圆锥的侧面展开图的圆心角度数为90°,母线长为40cm,则该圆锥的底面圆的半径为( )
A.9cmB.10cmC.11cmD.12cm
【答案】B【解析】设圆锥的底面圆的半径为rcm,则2πr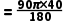 ,解得r=10,即圆锥的底面圆的半径为10cm.
,解得r=10,即圆锥的底面圆的半径为10cm.
14.【2025·云南】某书店今年3月份盈利6000元,5月份盈利6200元.设该书店每月盈利的平均增长率为x.根据题意,下列方程正确的是( )
A.6000(1+x)2=6200B.6000(1﹣x)2=6200
C.6000(1+2x)=6200D.6000x2=6200
【答案】A【解析】由题意可得,6000(1+x)2=6200.
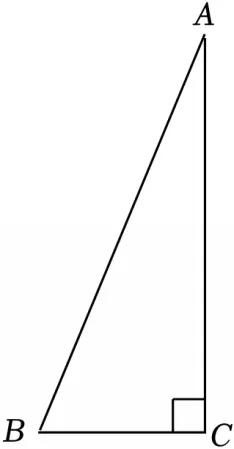
15.【2025·云南】如图,在Rt△ABC中,∠C=90°.若AB=13,BC=5,则sinA=( )
A. B.
B.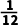 C.
C.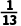 D.
D.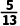
【答案】D【解析】∵在Rt△ABC中,∠C=90°.若AB=13,BC=5,∴sinA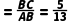 .
.
二、填空题:本题共4小题,每小题2分,共8分。
16.【2025·云南】已知⊙O的半径为5cm.若点P在⊙O上,则点P到圆心O的距离为cm.
【答案】5
17.【2025·云南】分解因式:x2+x= .
【答案】x(x+1)
18.【2025·云南】如图,四边形ABCD是菱形,对角线AC,BD相交于点O.若AC=6,BD=5,则菱形ABCD的面积是 .
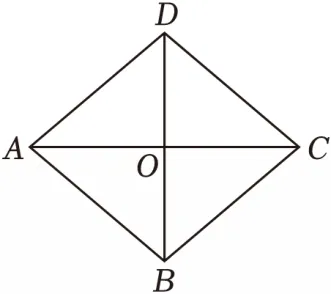
【答案】15【解析】∵四边形ABCD是菱形,AC=6,BD=5,∴菱形ABCD的面积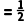 AC•BD
AC•BD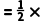 6×5=15.
6×5=15.
19.【2025·云南】某中学为了解全校1000名学生对新闻,娱乐,体育,动画,戏曲五类电视节目的喜爱情况,学校就“我最喜爱的电视节目”作了一次简单随机抽样调查.如图是根据调查结果绘制的扇形统计图.根据图中的信息,该校1000名学生中,最喜爱娱乐节目的学生大约有 名.

【答案】200【解析】该校1000名学生中,最喜爱娱乐节目的学生大约有1000×20%=200(名).
三、解答题:本题共8小题,共62分。解答应写出文字说明、证明过程或演算步骤。
20.【2025·云南】(7分)计算:(π﹣2)0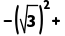 |﹣6|
|﹣6|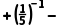 2cos60°.
2cos60°.
解:原式=1﹣3+6+5﹣2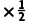
=1﹣3+6+5﹣1
=8.
21.【2025·云南】(6分)如图,AB与CD相交于点O,AC=BD,∠C=∠D.
求证:△AOC≌△BOD.
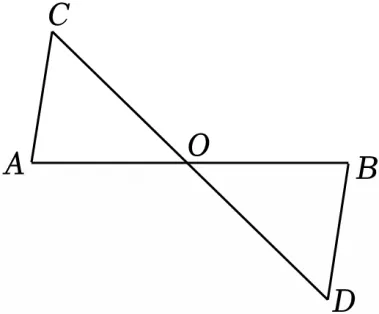
解:在△AOC和△BOD中,
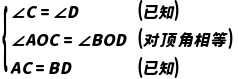 ,∴△AOC≌△BOD(AAS).
,∴△AOC≌△BOD(AAS).
22.【2025·云南】(7分)某化工厂采用机器人A,机器人B搬运化工原料,机器人A比机器人B每小时少搬运20千克,机器人A搬运800千克所用时间与机器人B搬运1000千克所用时间相等.求机器人A,机器人B每小时分别搬运多少千克化工原料.
解:设机器人A每小时搬运x千克化工原料,则机器人B每小时搬运(x+20)千克化工原料,
根据题意得: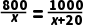
解得:x=80,
经检验,x=80是所列方程的解,且符合题意,
∴x+20=80+20=100(千克).
答:机器人A每小时搬运80千克化工原料,机器人B每小时搬运100千克化工原料.
23.【2025·云南】(6分)九年级某班学生计划到甲,乙两个敬老院开展献爱心活动,老师把该班学生分成A,B两个小组,通过游戏方式确定去哪个敬老院.
游戏规则如下:在一个不透明的箱子中放了分别标有数字1,2的两张卡片(除数字外,都相同),班长先从这个箱子里任意摸出一张卡片,卡片上的数字记为x.在另一个不透明的箱子中放了分别标有数字1,2,3的三张卡片(除数字外,都相同),班长再从该箱子里任意摸出一张卡片,卡片上的数字记为y.若x=y,则A组学生到甲敬老院,B组学生到乙敬老院;若x≠y,则A组学生到乙敬老院,B组学生到甲敬老院.
(1)用列表法或画树状图法中的一种方法,求(x,y)所有可能出现的结果总数;
(2)求A组学生到甲敬老院,B组学生到乙敬老院开展献爱心活动的概率P.
解:(1)画树状图如下:
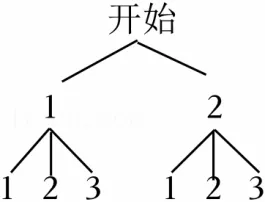
共有6种等可能的结果总数,即(1,1),(1,2),(1,3),(2,1),(2,2),(2,3);
(2)由(1)可知,共有6种等可能的结果,其中A组学生到甲敬老院,B组学生到乙敬老院开展献爱心活动的结果有2种,即(1,1),(2,2),
∴A组学生到甲敬老院,B组学生到乙敬老院开展献爱心活动的概率P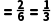 .
.
24.【2025·云南】(8分)如图,在△ABC中,∠ABC=90°,O是AC的中点.延长BO至点D,使OD=OB.连接AD,CD.记AB=a,BC=b,△AOB的周长为l1,△BOC的周长为l2,四边形ABCD的周长为l3.
(1)求证:四边形ABCD是矩形;
(2)若l2﹣l1=2,l3=28,求AC的长.
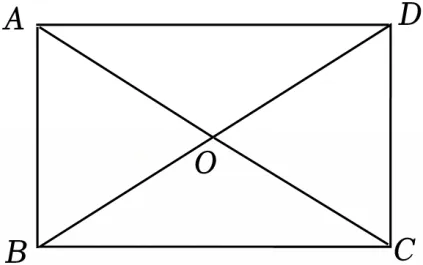
解:(1)证明:∵O是AC的中点,
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴平行四边形ABCD是矩形;
(2)∵记AB=a,BC=b,△AOB的周长为l1,△BOC的周长为l2,四边形ABCD的周长为l3,
∴l2﹣l1=BC﹣AB=b﹣a=2,l3=2(AB+BC)=2(a+b)=28,
∴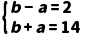
∴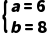
∴AB=6,BC=8,
∴AC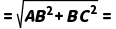 10.
10.
25.【2025·云南】(8分)请你根据下列素材,完成有关任务.
背景 | 某校计划购买篮球和排球,供更多学生参加体育锻炼,增强身体素质. |
素材一 | 购买2个篮球与购买3个排球需要的费用相等; |
素材二 | 购买2个篮球和5个排球共需800元; |
素材三 | 该校计划购买篮球和排球共60个,篮球和排球均需购买,且购买排球的个数不超过购买篮球个数的2倍. |
请完成下列任务: | |
任务一 | 每个篮球,每个排球的价格分别是多少元? |
任务二 | 给出最节省费用的购买方案. |
解:(任务一)设每个篮球的价格是x元,每个排球的价格是y元,
根据题意得: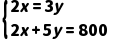 ,解得:
,解得: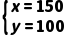 .
.
答:每个篮球的价格是150元,每个排球的价格是100元;
(任务二)设购买m个篮球,该校购买篮球和排球共花费w元,则购买(60﹣m)个排球,
根据题意得:w=150m+100(60﹣m)=50m+6000,
∵k=50>0,
∴w随m的增大而增大,
又∵60﹣m≤2m,解得:m≥20,
∴当m=20时,w取得最小值,此时60﹣m=60﹣20=40(个).
答:当购买20个篮球,40个排球时,总费用最低.
26.【2025·云南】(8分)已知a是常数,函数y=(x+4)(x﹣a2+a﹣3)+1,记T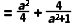 .
.
(1)若x=﹣4,a=1,求y的值;
(2)若x=3a+2,y=1,比较T与3的大小.
解:(1)把x=﹣4,a=1代入函数y=(x+4)(x﹣a2+a﹣3)+1,
得y=(﹣4+4)(﹣4﹣12+1﹣3)+1=1,
∴y的值为1;
(2)将x=3a+2,y=1代入函数,
得(3a+2+4)(3a+2﹣a2+a﹣3)+1=1,
整理得:﹣3(a+2)(a2﹣4a+1)=0,
①当a+2=0时,即a=﹣2,
∴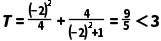
②当a2﹣4a+1=0时,a≠0,
则有a2=4a﹣1a2+1=4a,
∴a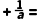 4,
4,
∴T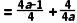
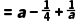
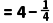
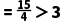
综上可知:当a=﹣2时,T<3;当a2﹣4a+1=0时,T>3.
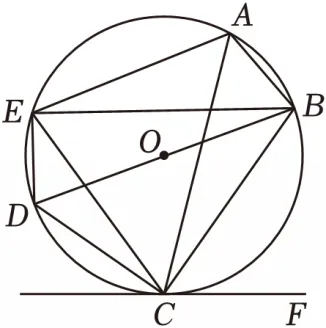
27.【2025·云南】(12分)如图,⊙O是五边形ABCDE的外接圆,BD是⊙O的直径.连接AC,BE,CE,∠AEC=∠ACF.
(1)若CE=CB,且∠CBE=60°,求∠BCE的度数;
(2)求证:直线CF是⊙O的切线;
(3)探究,发现与证明:
已知AC平分∠BAE,是否存在常数a,b,使等式AC2=aBC•CE+bAB•AE成立?若存在,请直接写出一个a的值和一个b的值,并证明你写出的a的值和b的值,使等式AC2=aBC•CE+bAB•AE成立;若不存在,请说明理由.
解:(1)∵CE=CB,且∠CBE=60°,
∴△CBE是等边三角形,
∴∠BCE=60°;
(2)证明:延长CO交⊙O于点M,连接EM,如图,
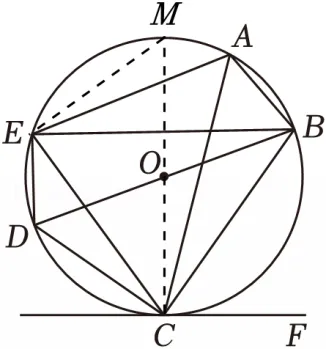
∵CM是⊙O的直径,
∴∠CEM=90°,
∴∠AEC+∠AEM=90°,
∵∠AEM=∠ACM,∠AEC=∠ACF,
∴∠ACF+∠ACM=90°,
∴∠MCF=90°,
∴OC⊥CF,
∵OC是⊙O的半径,
∴直线CF是⊙O的切线;
(3)存在常数a=1,b=1,使等式AC2=aBC•CE+bAB•AE成立;理由如下:
如图,设AC与BE交于点N,
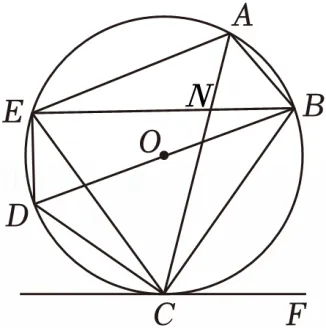
∵AC平分∠BAE,
∴∠EAC=∠BAC,
∵∠EAC=∠EBC,∠BEC=∠BAC,
∴∠EAC=∠EBC=∠BAC=∠BEC,
∴CE=CB,
∵∠BCN=∠ACB,∠CBE=∠BAC,
∴△BCN∽△ACB,
∴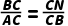
∴BC2=AC•CN①,
∵∠AEN=∠BEA,∠EAC=∠BAC,
∴△AEN∽△ACB,
∴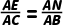
∴AE•AB=AC•AN②,
①+②得:BC2+AE•AB=AC•CN+AC•AN=AC(CN+AN)=AC2,
∵CE=CB,
∴AC2=BC•CE+AB•AE,
∴此时a=1,b=1.
∴存在常数a=1,b=1,使等式AC2=aBC•CE+bAB•AE成立.
解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2025/6/19 18:09:58;用户:初中数学;邮箱:17603237816;学号:63705528






