一、试题重现
23.(8分)【定义新运算】
对正实数a,b,定义运算“⊗”,满足a⊗b.
例如:当a>0时,(2a)⊗1.
(1)当a>0时,请计算:(2a)⊗(2a)=a;
【探究运算律】
对正实数a,b,运算“⊗”是否满足交换律a⊗b=b⊗a?
∵a⊗b,
b⊗a,
∴a⊗b=b⊗a.
∴运算“⊗”满足交换律a⊗b=b⊗a.
(2)对正实数a,b,c,运算“⊗”是否满足结合律(a⊗b)⊗c=a⊗(b⊗c)?请说明理由;
【应用新运算】
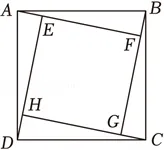
(3)如图,正方形ABCD是由四个全等的直角三角形和中间的小正方形EFGH拼成,AF=a,BF=b,且a>b.若正方形ABCD与正方形EFGH的面积分别为26和16,则(2a)⊗b⊗(2a)的值为.
二、试题解答
解:(1)由新定义得,(2a)⊗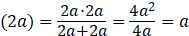 ,
,
故答案为:a;
(2)对正实数a,b,c,运算“⊗”满足结合律(a⊗b)⊗c=a⊗(b⊗c),
理由如下:左边:(a⊗b)⊗⊗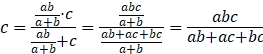 ,
,
右边: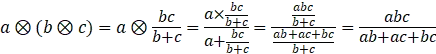 ,
,
∴左边=右边,
∴对正实数a,b,c,运算“⊗”满足结合律(a⊗b)⊗c=a⊗(b⊗c);
(3)由题意得,∠AFB=90°,
∴AF2+BF2=AB2,
∵AF=a,BF=b,且a>b,正方形ABCD的面积为26,
∴a2+b2=26,
∵四个直角三角形全等,
∴AE=BF=b,
∴EF=AF﹣AE=a﹣b,
∵正方形EFGH的面积为16,
∴(a﹣b)2=a2+b2﹣2ab=16,
∴26﹣2ab=16,
∴ab=5,
∴(a+b)2=(a﹣b)2+4ab=16+4×5=36,
∴a+b=6(舍负),
∴(2a)⊗b⊗(2a)=(2a)⊗(2a)⊗b=a⊗,
故答案为:.
三、课标体现与教学导向
这道以 “定义新运算⊗”为核心的考题,融合代数运算、运算律探究、数形结合等内容,紧扣《义务教育数学课程标准》对初中数学抽象、运算能力、推理能力、创新意识、几何直观等核心素养的培养要求,既考查了数与式、勾股定理、正方形面积等基础知识,又突出了探究性、综合性、迁移性的命题特点,充分体现了新课标重视过程、融合知识、发展能力的核心理念,同时为初中数学教学明确了强化抽象、注重探究、融数于形、培养迁移的实施方向。
(一)新课标体现
1.聚焦核心素养,全方位发展初中数学关键能力
本题以新运算定义为载体,让学生经历理解定义、运用定义、探究规律、综合应用的过程,
数学抽象体现在要求学生从文字与符号定义中,抽象出新运算的数学本质,将新运算转化为常规的分式乘除与加减运算,培养学生对数学符号和新规则的抽象理解能力。运算能力体现在考查分式的通分、约分、化简,完全平方公式的灵活运用,以及结合新运算规则的分步运算。推理能力体现在探究交换律、结合律时,要求学生从新运算定义出发,通过演绎推理分别推导相等性,步步推导,培养学生的逻辑推理与论证能力。创新意识体现在创设全新的运算规则,要求学生打破已有运算的思维定式,迁移已有知识解决新问题,同时将新运算与几何图形结合,培养学生在新情境下的数学应用与创新能力。几何直观体现在将正方形拼接的几何图形转化为勾股定理、面积关系的代数表达式,通过几何图形直观感知数量关系,再转化为代数运算求解,落实数形结合的核心要求。
2.强化知识融合,体现代数与几何的整体性
新课标倡导强调知识的综合性与关联性,本题实现了多领域知识的有机融合。
将新运算的分式运算、乘法公式、代数式变形代数内部的融合,考查学生对代数知识的综合运用能力。第三问以 “赵爽弦图” 式的正方形拼接为背景,将正方形面积、勾股定理的几何知识,转化为代数关系,再结合新运算求解,让学生体会代数与几何的相互转化。
将“运算律探究”的方法迁移到新运算中,让学生体会交换律、结合律的通用探究思路,实现知识与方法的融合。
3.注重过程性探究,落实新课标过程与结果并重的目标
新课标强调让学生经历数学知识的形成与探究过程,交换律的探究给出了完整的推导示范,引导学生掌握从定义出发,分别表示两边表达式,验证相等的探究方法。结合律的探究要求学生自主完成上述推导过程,经历理解规则、猜想结论、分步推导、得出结论的探究流程,这种设计让学生掌握探究数学规律的通用方法。
4.突出知识迁移,培养以旧知解新的数学能力
新课标强调学生能运用已有的知识和经验解决新问题,本题的核心考查点之一就是知识迁移能力。
(二)教学导向
1.培养数学抽象与符号意识,强化新定义问题的教学
新定义问题是考查数学抽象和符号意识的重要载体,教学中应注重引导学生理解新定义、转化新定义、运用新定义。设计多样化的新定义问题,培养学生的符号意识和抽象理解能力,提升学生在新情境下的数学适应能力。
2.强化运算能力的综合性培养
运算能力是初中数学的基础能力,教学中应转向综合性、技巧性、严谨性的运算能力培养。
强化分式的通分、约分、化简,乘法公式的灵活运用,勾股定理与面积关系的转化,确保学生的基础运算准确、规范。引导学生运用运算律化简复杂运算,学会观察式子特征,选择最优的运算方法。设计代数与几何融合的运算问题,让学生学会将几何数量关系转化为代数运算,提升综合运算能力。
3.重视探究性教学,让学生经历完整过程
教学中应将探究融入日常教学,尤其是运算律、数学规律、公式推导等内容,避免直接告知结论。以运算律、公式等为载体,设计探究性活动,引导学生经历提出猜想、自主推导、验证结论、总结方法的探究过程。鼓励学生大胆猜想、严谨验证,培养学生的推理能力和探究精神,让学生在探究中理解数学知识的形成过程。
4.落实数形结合思想,打破代数与几何的孤立教学
代数与几何是初中数学的两大核心领域,二者相互关联、相互转化,教学中应打破二者的壁垒,实现数形融合教学。在代数教学中融入几何直观,如用图形解释乘法公式、用数轴理解实数、用函数图象理解函数性质,让代数知识更直观。在几何教学中融入代数运算,如用勾股定理、相似、全等转化为代数数量关系,用代数运算解决几何求值、证明问题,让几何问题更易解。







