解析26年上海中考宝山区一模数学试卷

解析26年上海中考宝山区一模数学试卷

反映了2026年上海中考的命题趋势：

1、“新定义”题型常态化：

无论是填空第18题的“差直三角形”还是第24题的“子抛物线”，都在考察学生现场学习能力。遇到陌生名词不要怕，严格按照题目给出的定义去“翻译”数学语言。建议： 训练快速阅读数学定义的能力，学会举一反三。

2、强调“数学建模”与“跨学科”：

第22题（自行车）和第6题（小孔成像）都说明，数学不再是枯燥的计算，而是解决实际问题的工具。建议： 多关注生活中的几何模型（如折叠、测量、运动轨迹），学会把文字语言转化为图形语言。

3、压轴题重在“分类讨论”：

最后两道大题的第(3)问，核心考点都是分类讨论。这是上海卷拉开分差的关键。建议： 养成画图标注的习惯，动点问题要按“左、中、右”或“上、下”位置分类，等腰三角形/直角三角形存在性问题要按“边边相等/角角相等”分类，做到不重不漏。

第18题（重难点）：“差直三角形”。 这是一个新定义题型（有两个内角差为90°）。结合已知tanc=3/4和BC=4。需要进行分类讨论。很多学生容易漏解或无法理解新定义，导致失分。

第24题（函数压轴）：“子抛物线”新定义。

定义了一个新概念——将抛物线绕顶点旋转180度再平移得到“子抛物线”。第②问涉及动点与平行四边形存在性问题。需要理解“旋转180度”即关于某点中心对称的几何本质，并结合代数计算。考察数形结合与新概念接受能力。

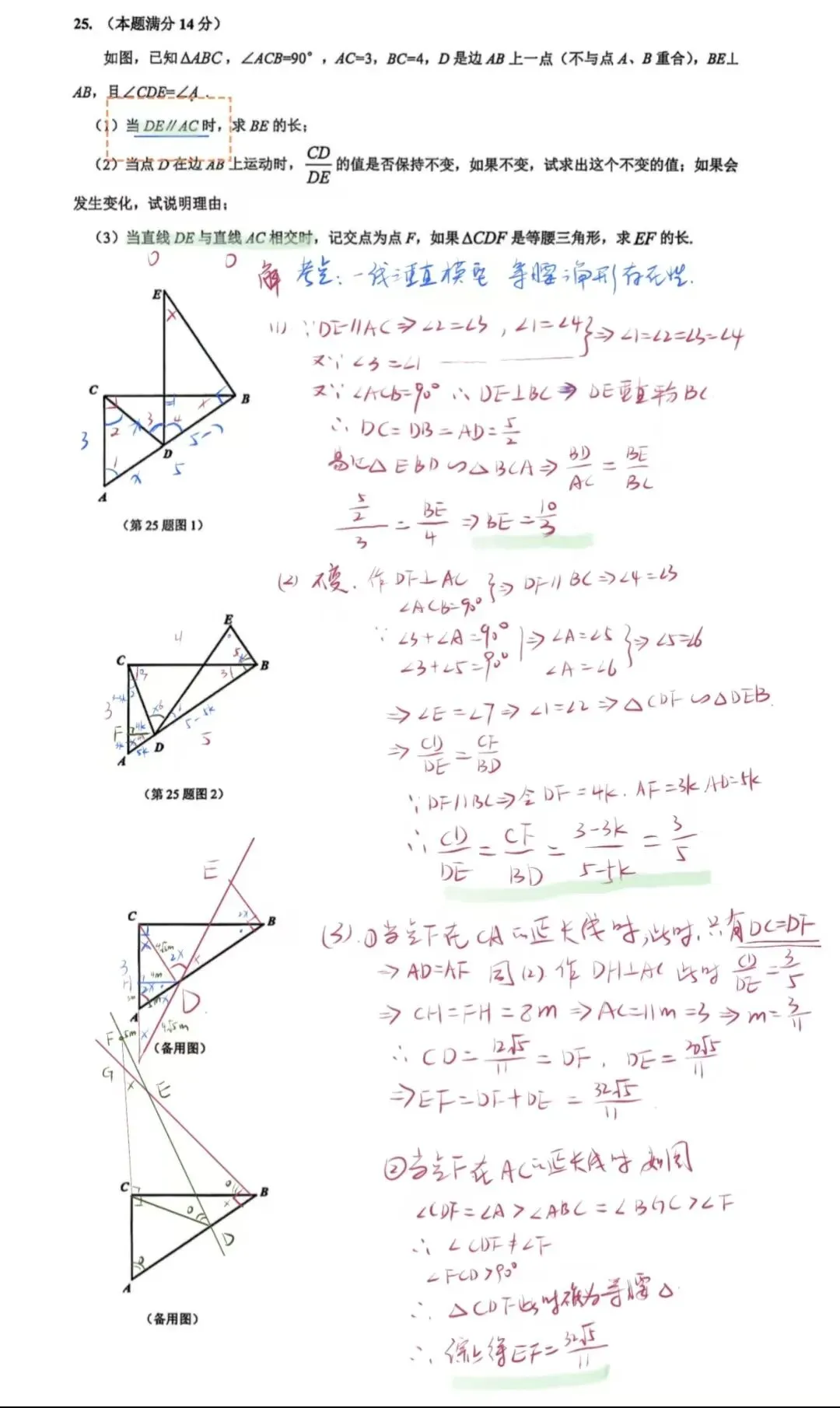
第25题（几何压轴）：动点与等腰三角形。背景是经典的直角三角形。第(2)问探究比值是否变化，本质是考察“一线三等角”模型的变式，需要证明相似。第(3)问是全卷最难处：当是等腰三角形时，求线段长。需要分类讨论（哪两条边相等？）。