
文章中的公式丢失,请在文末下载word完整电子版
①平等与对称
②旋转
③折叠
④坐标与尺规作图
 平行与对称
平行与对称
1.(2024·云南昭通·二模)文字是传承人类文明的重要媒介,我国的汉字传承了数千年之久,是各国文字中的佼佼者.下列汉字中,既可以看作轴对称图形,又可以看作中心对称图形的是( )
A. B.
B. C.
C. D.
D.
2.(2024·内蒙古包头·二模)如图,已知,则的度数是()
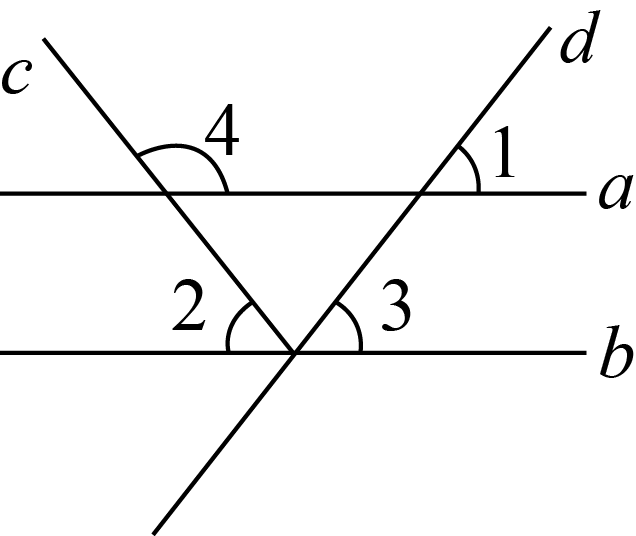
A.B.C.D.
3.(2024·宁夏银川·二模)凸透镜是中央较厚边缘较薄的透镜,如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线交于点P,点F为焦点,若,,则的度数是()
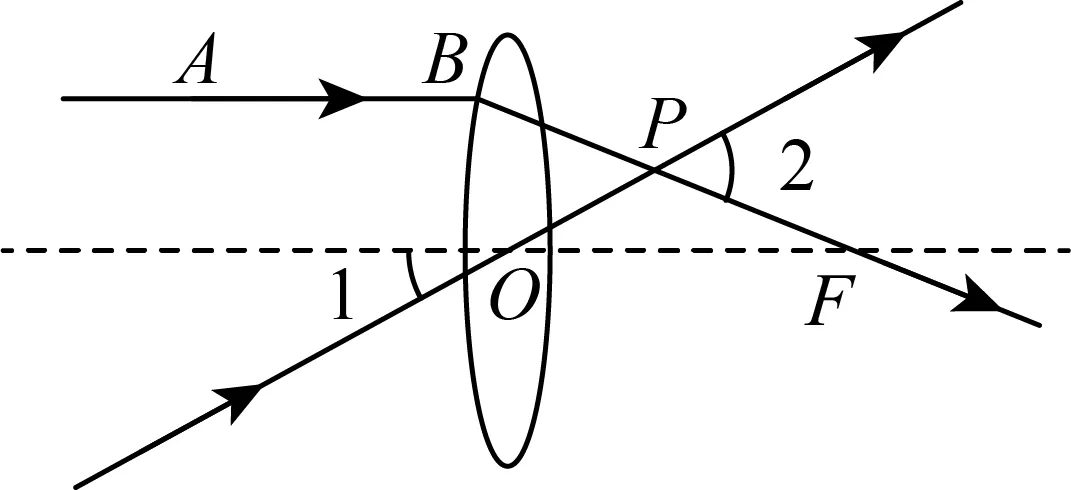
A.B.C.D.
4.(2024·山东济宁·二模)如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则的度数等于()
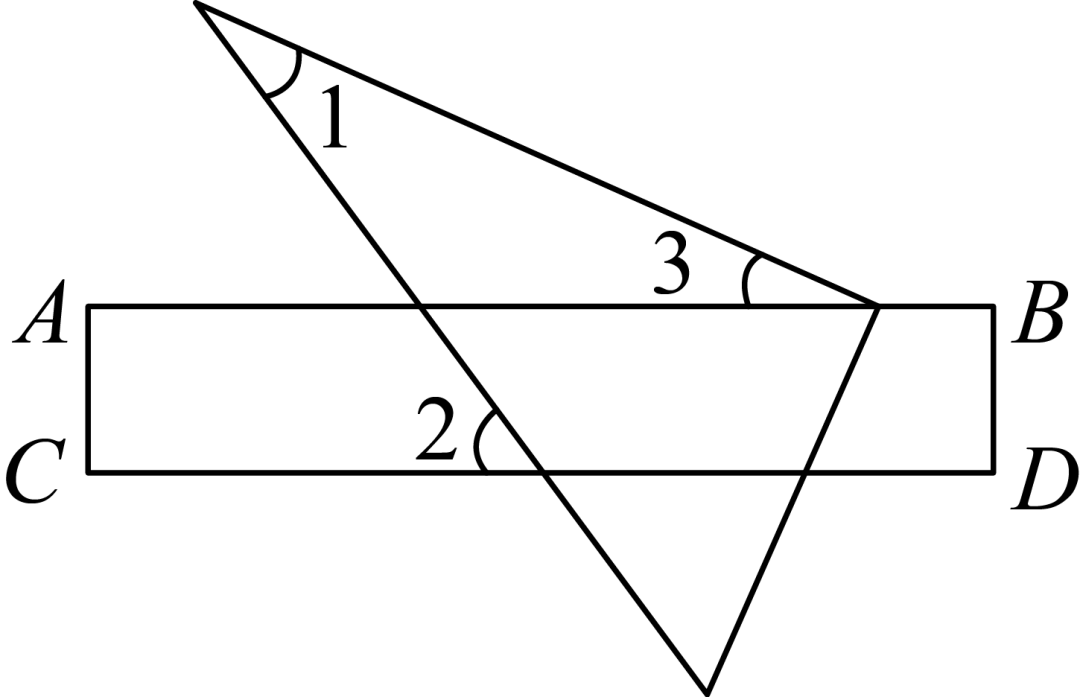
A.50°B.30°C.20°D.15°
5.(2023·浙江金华·二模)如图,于A,,若,则等于( )
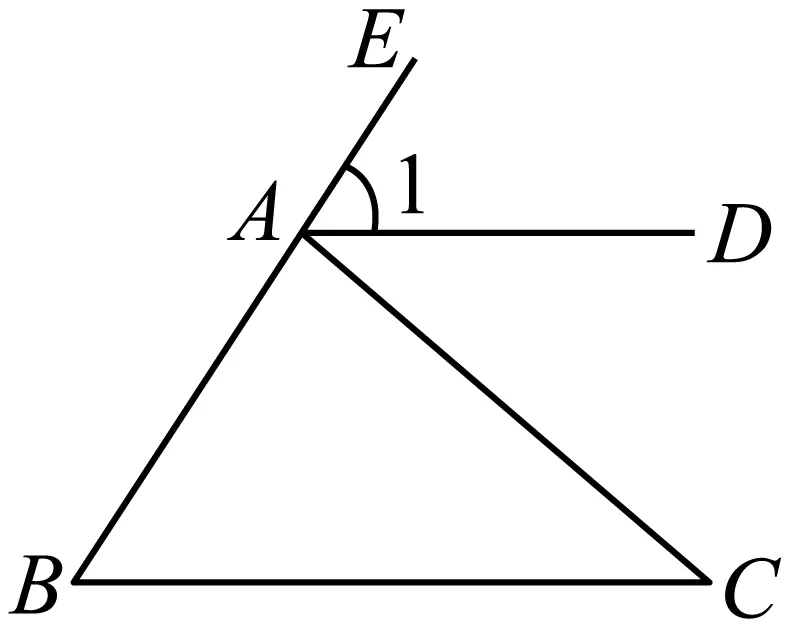
A. B. C. D.
6.(2024·商丘夏邑·二模)如图,直线,,,则的度数为( )
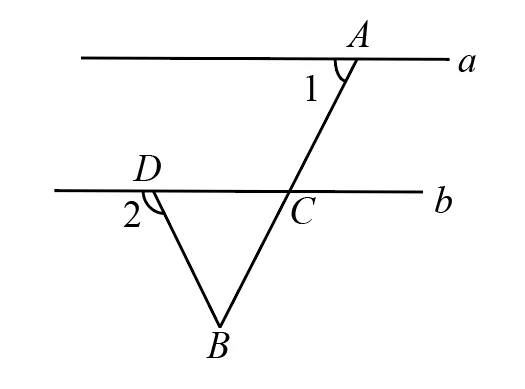
A.B.C.D.
7.(2024·山东日照·二模)数学中处处存在着美,从三国时期的赵爽弦图,到19世纪的莱洛三角形,再到近代的科克曲线和谢尔宾斯基三角形,这种特殊的数学之美,令人沉迷.下列图形中,既是中心对称图形,又是轴对称图形的是()
A.赵爽弦图 B.莱洛三角形
B.莱洛三角形
C.科克曲线 D.谢尔宾斯基三角形
D.谢尔宾斯基三角形
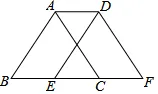
8.(2024·山东济宁·二模)如图,将周长为8的△ABC沿BC方向向右平移1个单位得到△DEF,则四边形ABFD的周长为.
9.(2024·江苏镇江·二模)如图,在、两地间修一条笔直的公路,从地测得公路的走向为北偏东,如果 、两地同时开工,那么为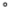
 旋转
旋转
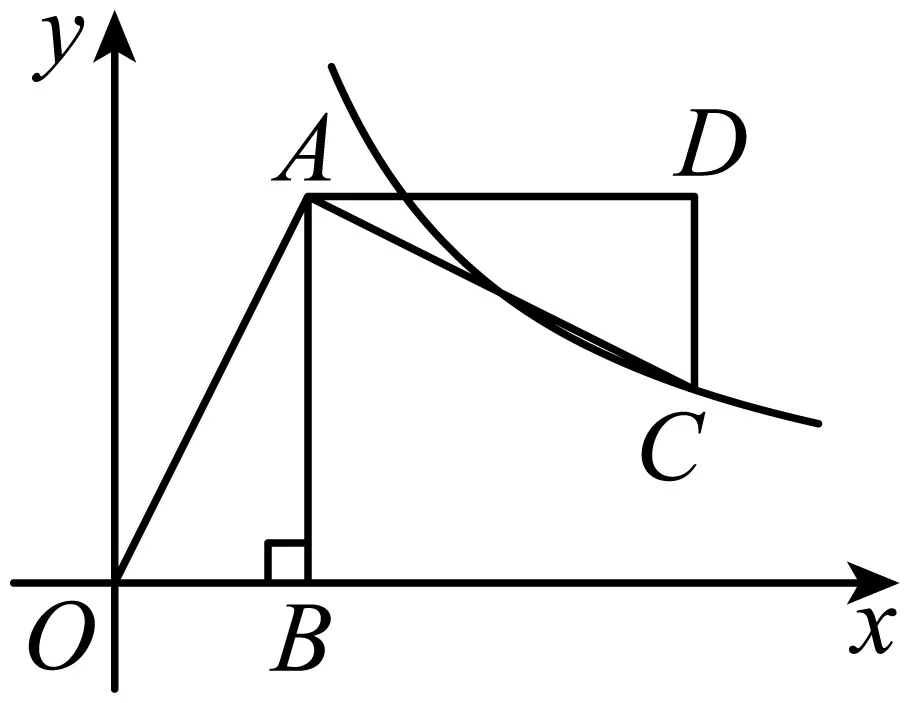
10.(2024·山东济宁·二模)如图,平面直角坐标系中,在轴上,,点的坐标为(1,2),将绕点 逆时针旋转,点的对应点恰好落在双曲线上,则的值为()
A.2B.3C.4D.6
11.(2024·河南南阳·二模)如图,将菱形绕其对角线的交点顺时针旋转后,再向右平移3个单位,则两次变换后点C对应点的坐标为()
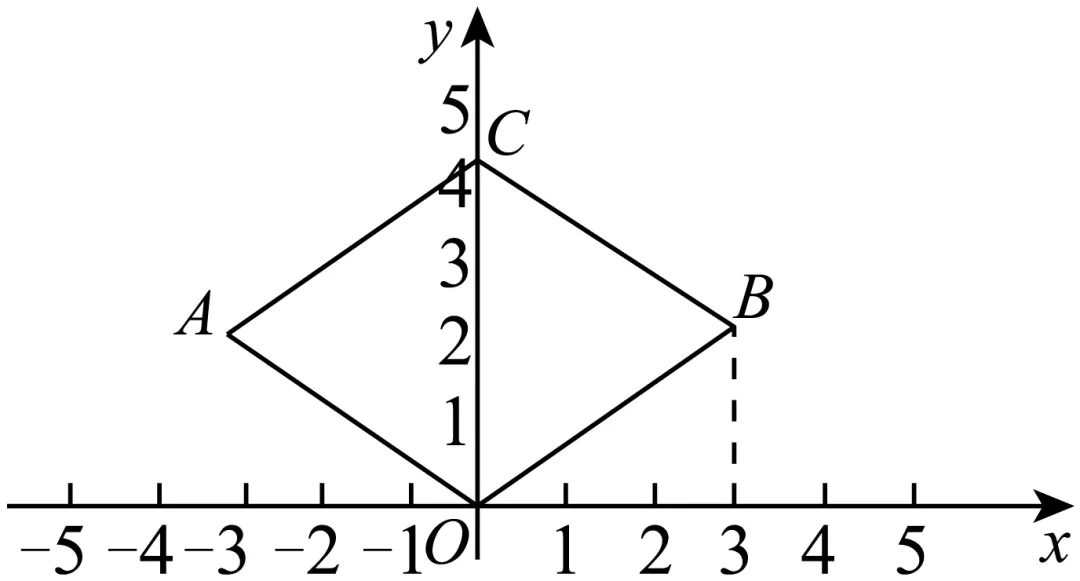
A.B.C.D.
12.(2024·内蒙古包头·二模)如图,正方形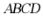 的边长为4,点
的边长为4,点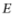 是
是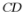 的中点,
的中点,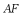 平分
平分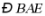 交
交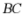 于点
于点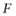 ,将
,将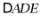 绕点
绕点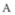 顺时针旋转90°得
顺时针旋转90°得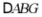 ,则
,则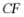 的长为.
的长为.
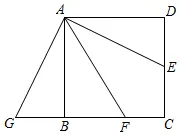
13.(2024·宁夏银川·二模)图形的旋转变换是研究数学相关问题的重要手段之一,小华和小芳对等腰直角三角形的旋转变换进行了研究.如图①,已知和均为等腰直角三角形,E分别在线段,上,且.

(1)观察猜想小华将绕点A逆时针旋转,连接,,如图②,当点E与点F重合时:
①的值为______;
②的度数为______度;
(2)类比探究:如图③,小芳在小华的基础上继续旋转,连接,(1)中的两个结论是否仍然成立?请说明理由;
(3)拓展延伸:若,当所在的直线垂直于时,直接写出的长.
14.(2024·宁夏银川·二模)如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,,,解答下列问题:

(1)将线段绕原点顺时针方向旋转得到线段,再将线段向下平移2个单位长度得到线段,画出线段和线段;
(2)如果线段旋转可以得到线段,则旋转中心P的坐标为_______.(A和E是对应点)
15.(2024·广东惠州·二模)综合探究
【问题情境】几何探究是培养几何直观、推理能力和创新意识的重要途径.解决几何综合探究问题,往往需要运用从特殊到一般、化静为动、类比等数学思想方法.
【初步探究】
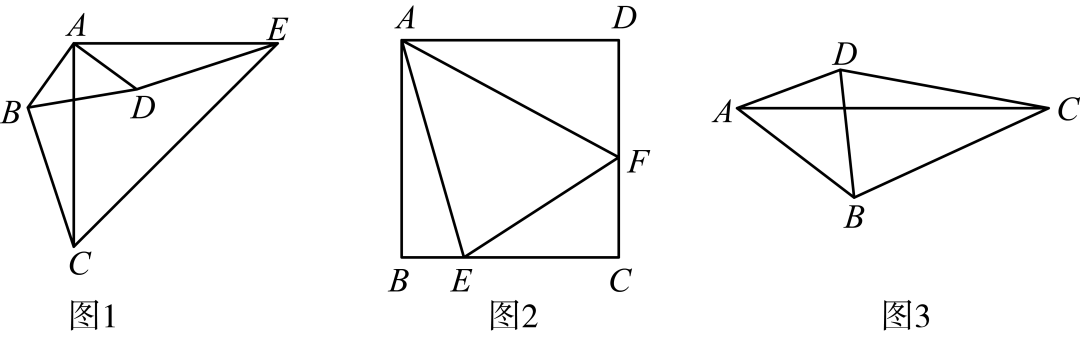
(1)如图1,将绕点逆时针旋转得到,连接,,根据条件填空:
①的度数为 ;
②若,则的长为 ;
【类比探究】
(2)如图2,在正方形中,点在边上,点在边上,且满足,,,求正方形的边长;
【拓展延伸】
(3)如图3,在四边形中,,,,为对角线,且满足,若,,请求出的长.
16.(2024·山东日照·二模)问题背景:在课外小组活动中,“创新小组”对“正方形旋转”问题进行了探究,如图,边长为的正方形的对角线相交于点,分别延长到点,到点,使,再以为邻边做正方形,连接;
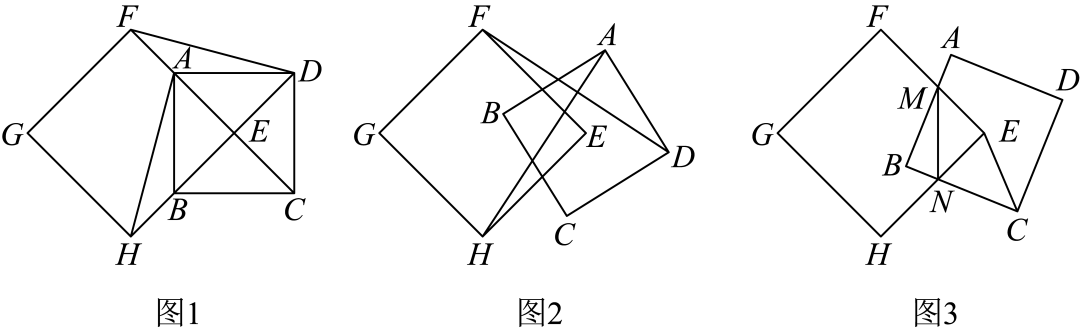
(1)解决问题:与之间的数量关系是______,位置关系是______;
(2)深入研究:如图正方形固定不动,将正方形绕点顺时针方向旋转,判断与的关系,并证明:
(3)拓展延伸:如图,在正方形旋转过程中,分别交于点,连接.当时,求的值.
17.(2024·浙江杭州·二模)将一副直角三角板与叠放在一起,如图1,,,,.在两三角板所在平面内,将三角板绕点O顺时针方向旋转()度到位置,使,如图2.
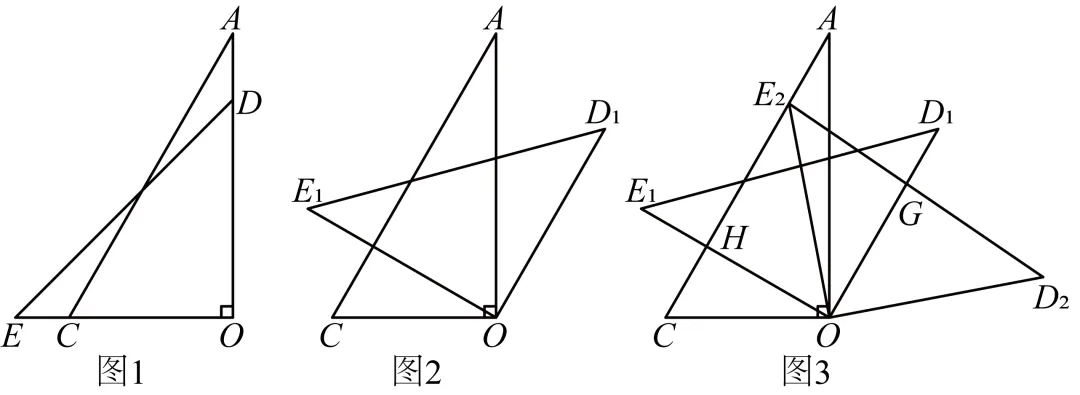
(1)求的值;
(2)如图3,继续将三角板绕点O顺时针方向旋转,使点E落在边上点处,点D落在点处.设交于点G,交于点H,若点G是的中点,试判断四边形的形状,并说明理由.
 折叠
折叠
18.(2024·河南信阳·二模)如图,中,是的中线,是边上一动点,将沿折叠,点落在点处,交线段于点,当是直角三角形时,.
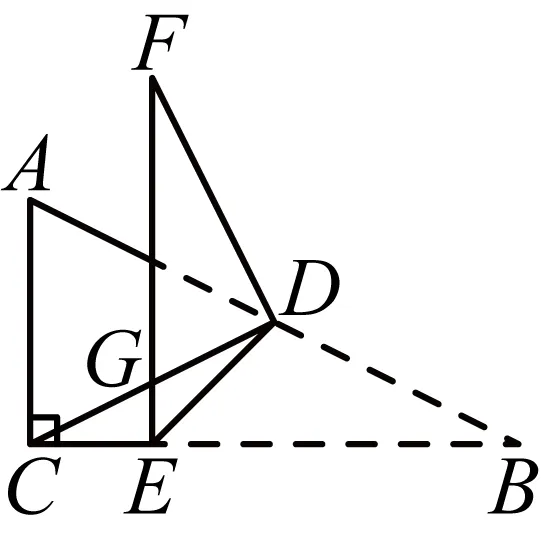
19.(2024·浙江杭州·二模)已知矩形纸片,将纸片沿折叠,使点与边上的点重合,展开纸片,连结,,与相交于点.将纸片继续沿折叠,点的对应点恰好落在上,展开纸片,连结,与交于点.已知,,则;.
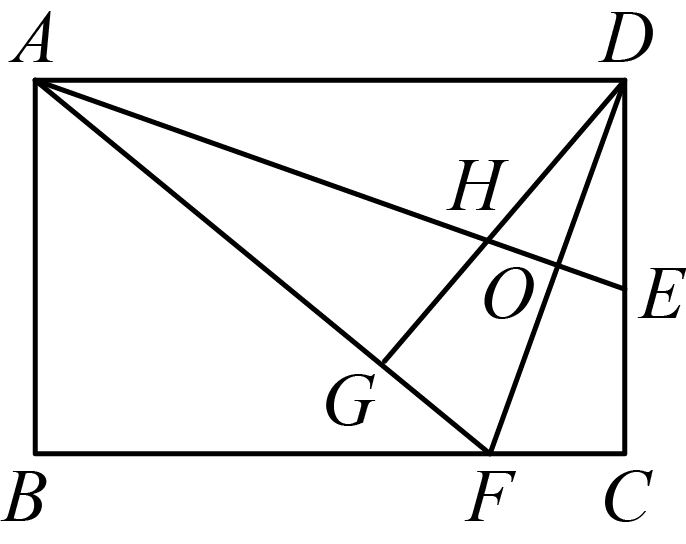
20.(2024·山东日照·二模)如图,在等腰中,,,为边的中点,为边上的一个动点,连接,将沿折叠,点的对应点为.当时,的长度为.
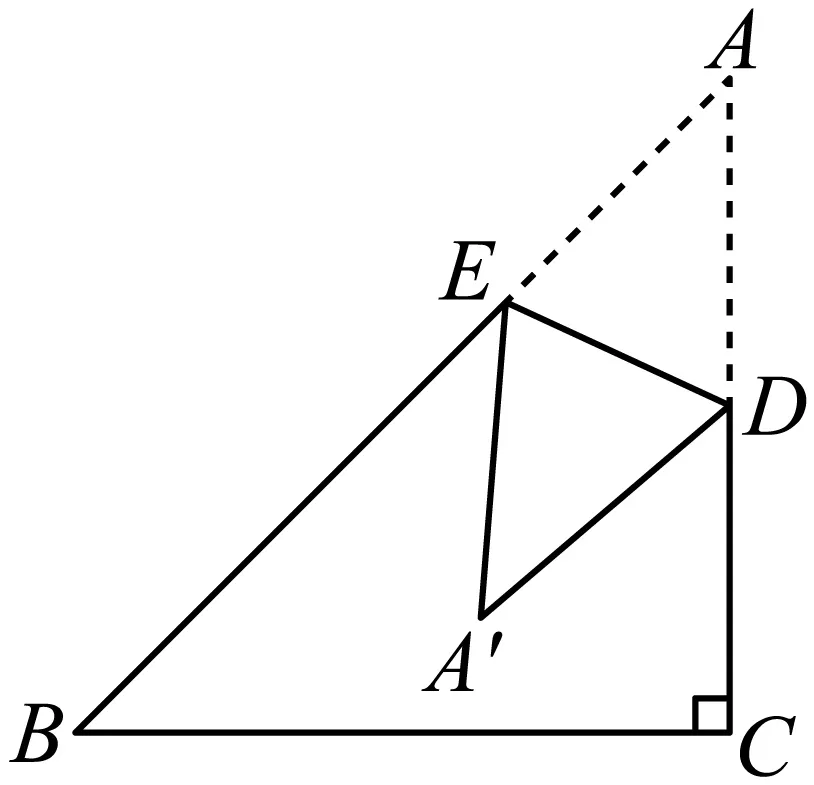
21.(2024·浙江杭州·二模)如图,腰长为22的等腰ABC中,顶角∠A=45°,D为腰AB上的一个动点,将ACD沿CD折叠,点A落在点E处,当CE与ABC的某一条腰垂直时,BD的长为.
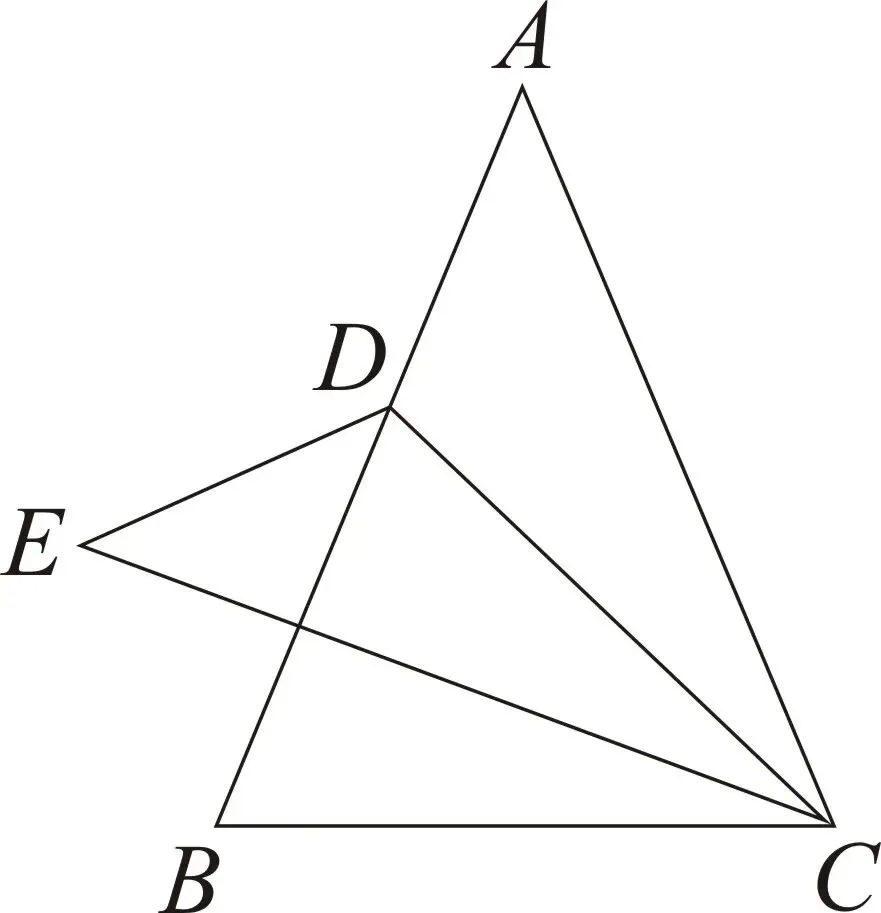
22.(2024·内蒙古包头·二模)如图①.在矩形.,点在边上,且.动点从点出发,沿折线以每秒个单位长度的速度运动,作,交边或边于点,连续.当点与点重合时,点停止运动.设点的运动时间为秒.()
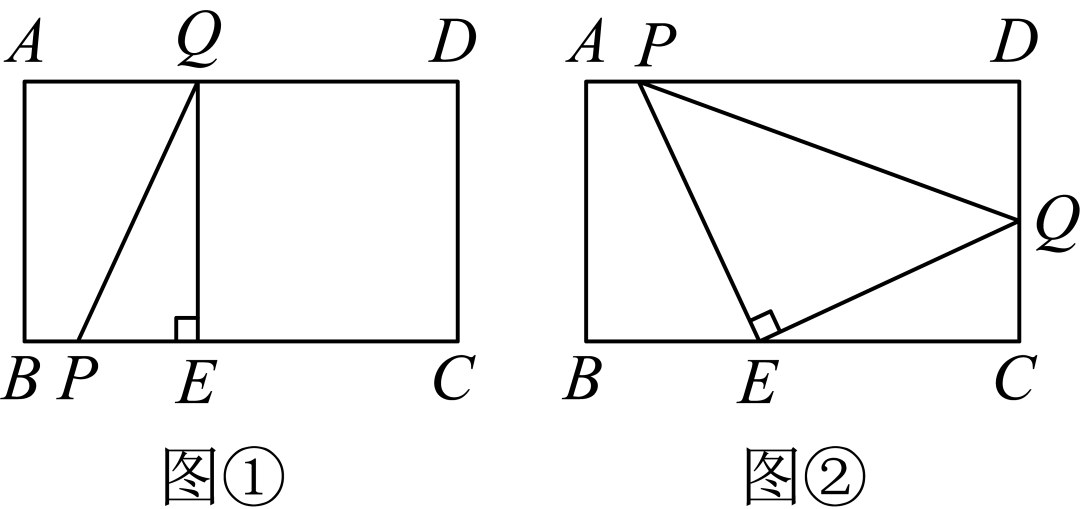
(1)当点和点重合时,线段的长为__________;
(2)当点和点重合时,求;
(3)当点在边上运动时,的形状始终是等腰直角三角形.如图②.请说明理由;
(4)作点关于直线的对称点,连接、,当四边形和矩形重叠部分图形为轴对称四边形时,直接写出的取值范围.
23.(2024·江苏镇江·二模)“折纸”是同学们经常做的手工活动.
如图1,矩形纸片,,点O为其对称中心,小明沿着过点 O 的直线将矩形纸片进行折叠,折痕交边于点 M、N,点A、B的对应点记为交边于点E.
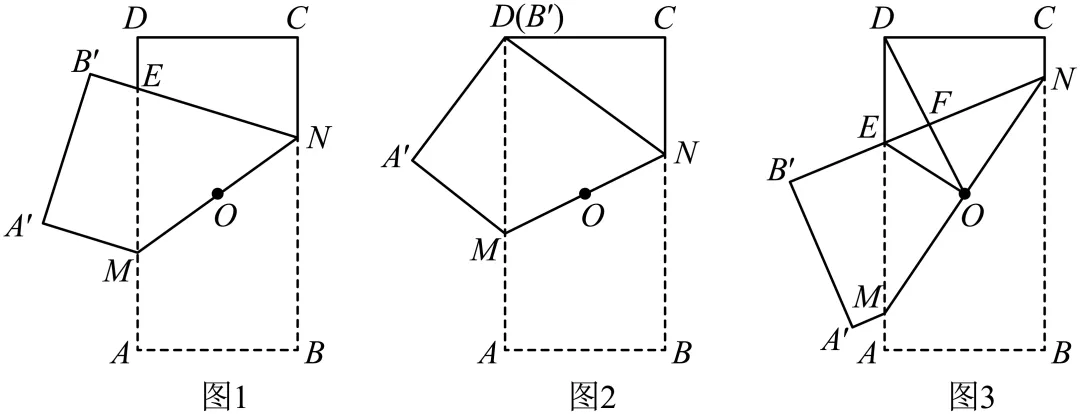
(1)如图2,当点与点D重合时,;
(2)在上述折叠过程中,求证:
①为等腰三角形;
② ;
(3)如图3,,连结交于点F,连接,则的面积为.
 坐标与尺规作图
坐标与尺规作图
24.(2024·浙江杭州·二模)如图所示,若点坐标为,则对应的点可能是()
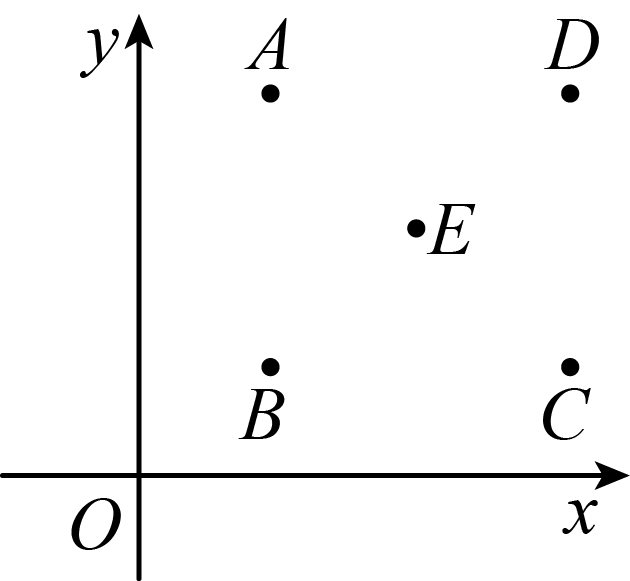
A.点B.点C.点D.点
25.(2024·浙江温州·二模)尺规作图源于古希腊的数学课题,蕴含着丰富的几何原理.如图,在中,按如下步骤尺规作图:①以点B为圆心,为半径作弧交边于点D;②以点A为圆心,为半径作弧交于点E;③连结与.若要求的度数,则只需知道()
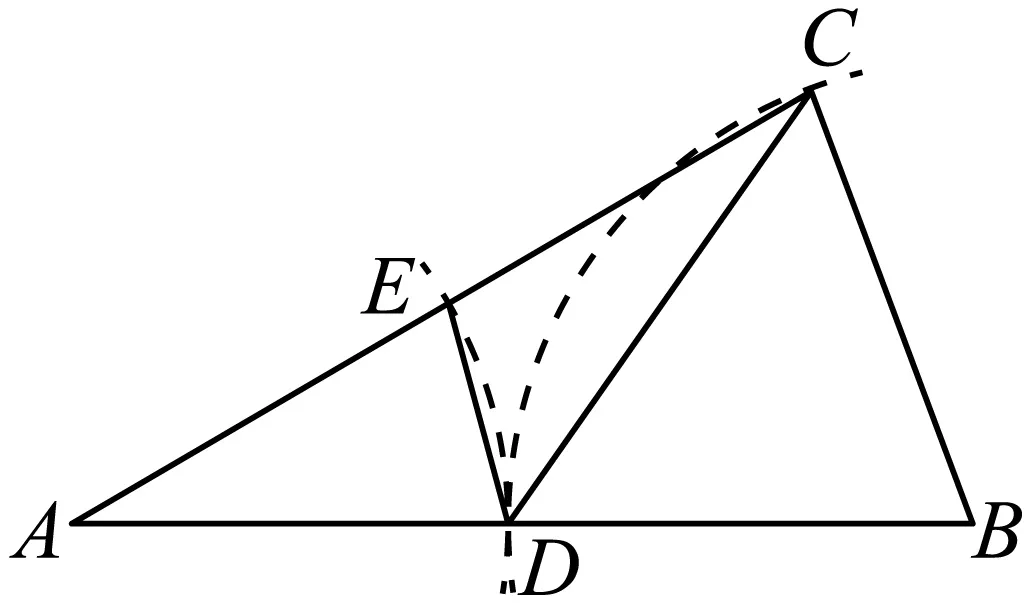
A.的度数B.的度数
C.的度数D.的度数
26.(2024·宁夏银川·二模)如图,在平面直角坐标系中,各坐标分别为,,,,,,,,,,,则依图中所示规律,的坐标为()
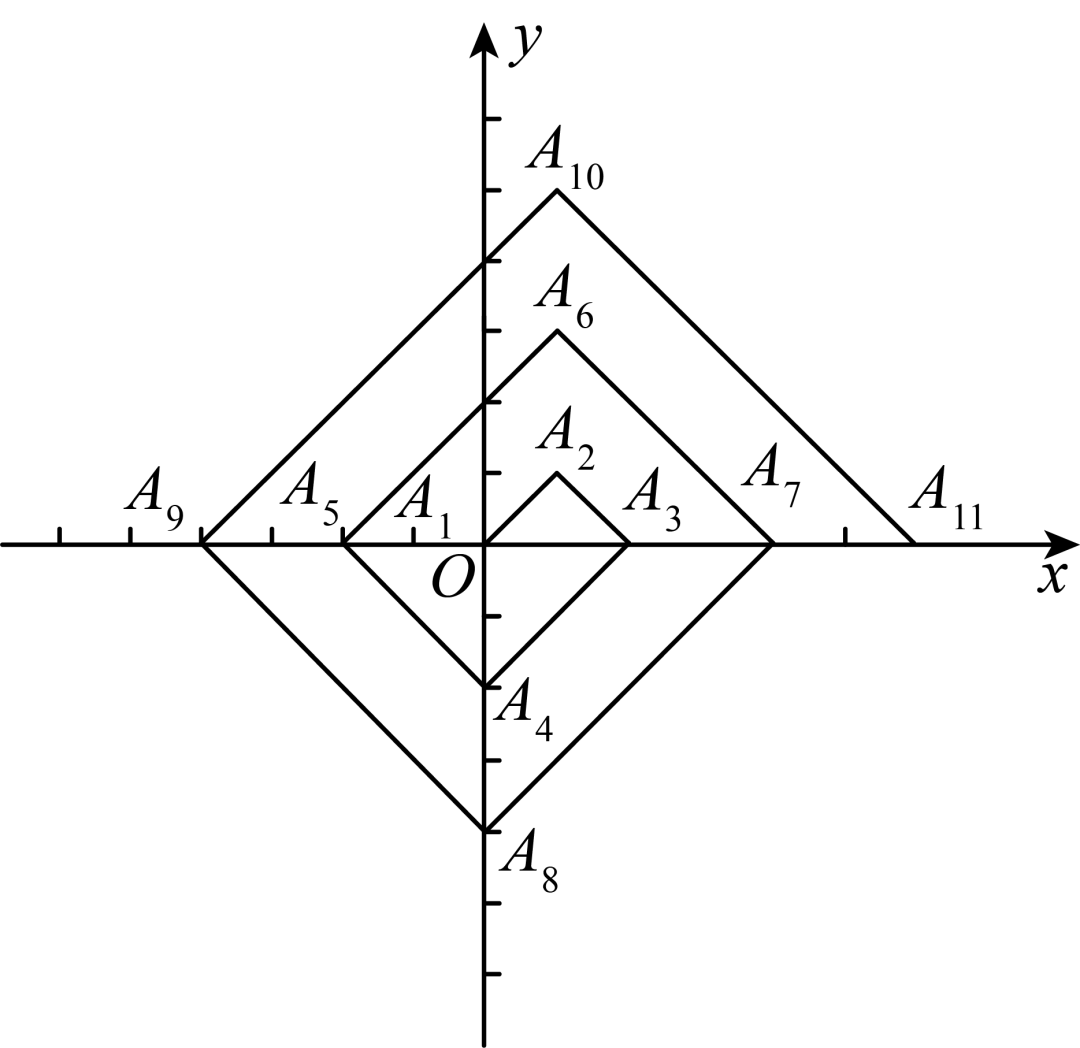
A.B.C.D.
27.(2024·河南新乡·二模)如图是由小正方形组成的网格,每个小正方形的顶点叫做格点.
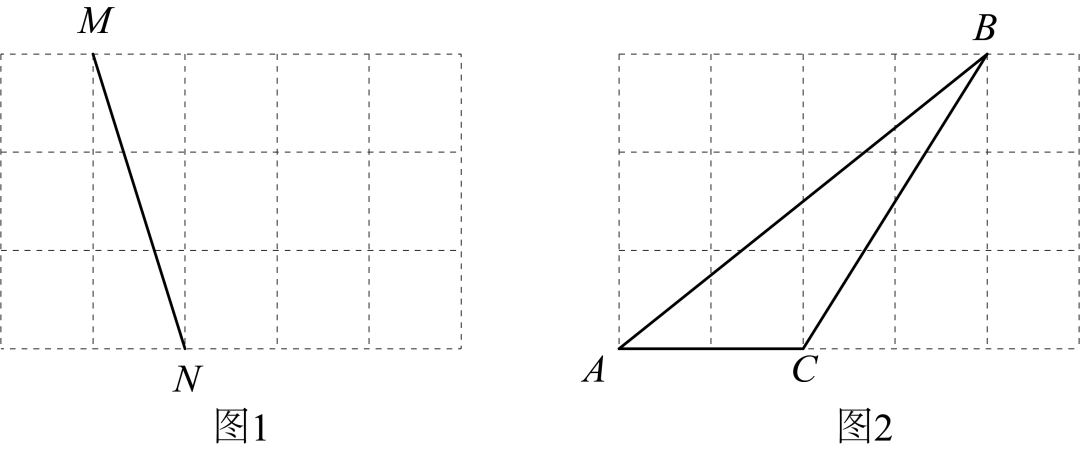
(1)图1中点都是格点,请仅用无刻度的直尺作出的中点,要求保留作图痕迹,不写作法.
(2)图2中的三个顶点都是格点,请仅用无刻度的直尺作出的角平分线,要求保留作图痕迹,不写作法.(要求:的角平分数用实线表示,其它线用虚线表示.)
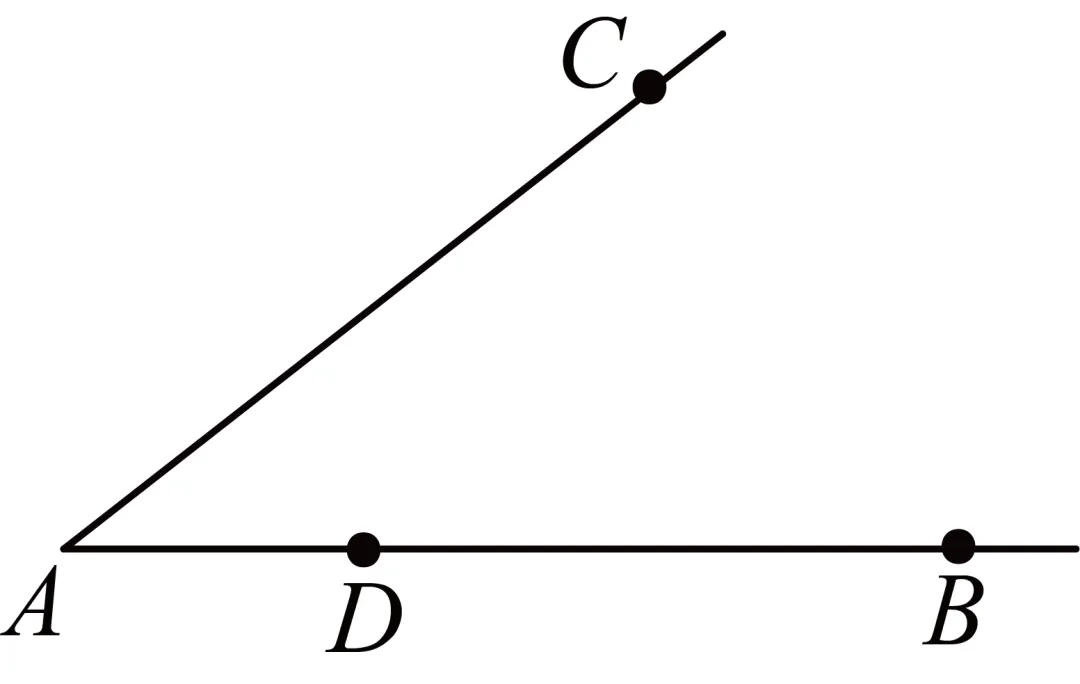
28.(2024·陕西西安·二模)如图,在中,,,为上一点,且,利用圆规和无刻度直尺在线段上找一点,使得.(保留作图痕迹,不写作法)
29.(2024·浙江杭州·二模)如图,在的正方形网格图中,小正方形的边长都为1,的顶点都在格点上,在该网格图中只用无刻度的直尺作图,保留作图痕迹.

(1)在线段上画出点,使.
(2)画出的外接圆圆心,并连接,,求弧的长
30.(2024·广东惠州·二模)如图,在中,.
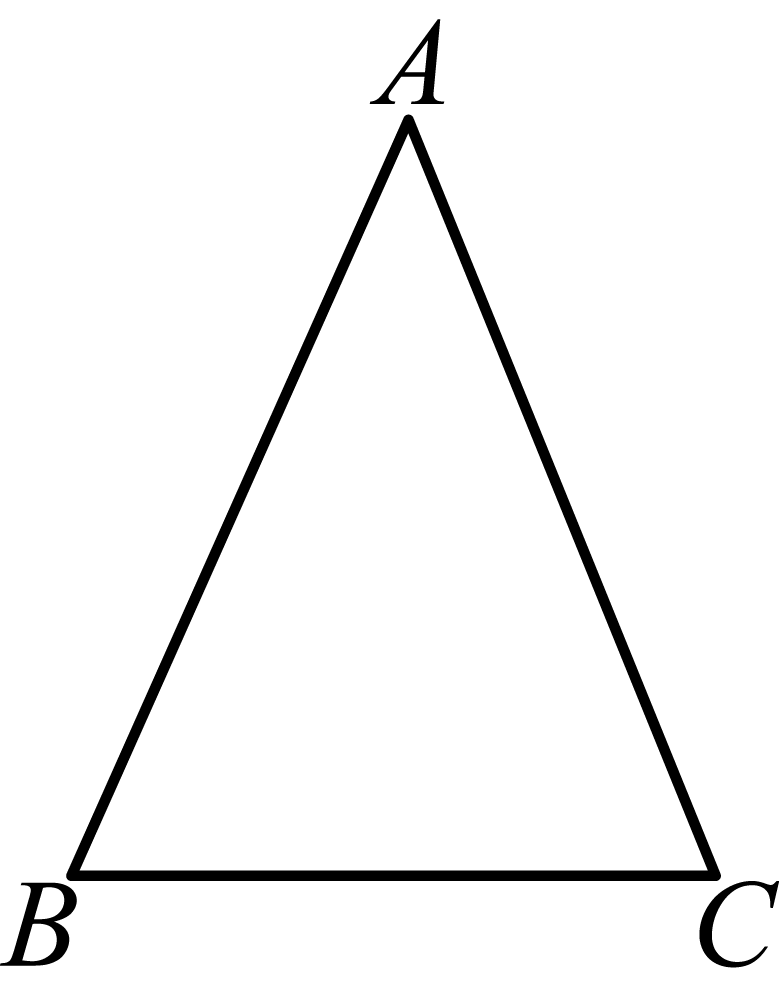
(1)实践与操作:在边上找一点D(点C,D不重合),使得为等腰三角形(尺规作图,保留作图痕迹);
(2)猜想与证明:在(1)的条件下,试猜想之间的数量关系,并加以证明.
31.(2024·浙江杭州·二模)如图,在中,平分.
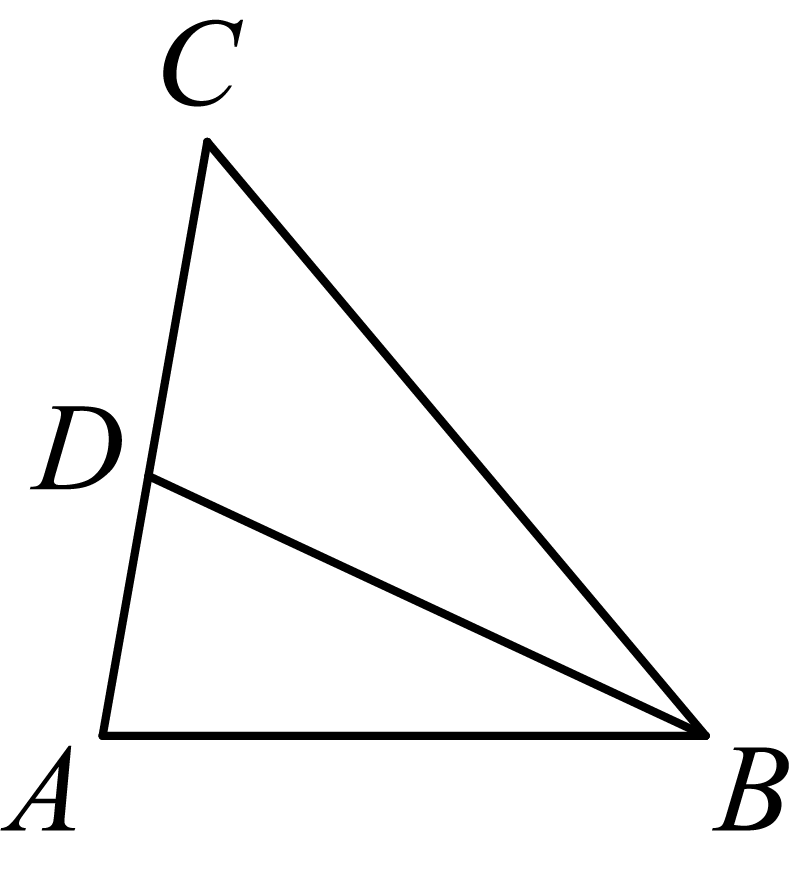
(1)作交于点.(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:.
word完整电子版下载方式:
关注公众号,发送消息:261271







