
点击箭头处“蓝色字”,关注我们哦!!

一、黄卫民老师的教学理念与命题思路
1. 教学理念与命题逻辑的内在关联
黄卫民老师从教21年来,形成了独特的"以德施教与能力培养结合"的育人理念。这一理念体现在命题中,主要表现为:
知识为本,思维为用:黄卫民老师认为,数学教学应"言学习之重本",即重视基础知识的掌握,同时"传师德而育人",将德育贯穿于解题过程中。这与其命题风格高度一致——基础题占比高,但压轴题注重思维引导而非单纯计算。
从特殊到一般的探究式学习:黄卫民老师强调,数学学习应通过具体案例理解抽象概念,再逐步推广到一般情况。这种教学思路很可能影响其命题设计,即压轴题通常以简单情形入手,再逐步深入探究,引导学生发现规律。
教学与命题的一致性:黄卫民老师曾提出,小学数学的"1+1=2"是定量关系,初中数学的)x+1=2"是变量关系,高中数学的)x+y=2"则是讨论思想的培养。这种对不同学段数学思维特点的认识,很可能体现在中考命题中,使试题既符合初中数学水平,又为高中数学学习做好铺垫。

2. 自创教学方法在命题中的体现
黄卫民老师自创的"名称概念教学法"和"庖丁解牛解题法",很可能成为其命题设计的核心方法论:
名称概念教学法:通过解析数学概念名称的字面含义,降低学生理解难度。这种方法很可能体现在中考命题中,特别是新定义题型的设计上。命题人会通过简明扼要的题干描述,引导考生从概念名称入手理解题意,而非直接给出复杂的数学定义。
庖丁解牛解题法:将复杂数学问题拆解为可操作的步骤,提升解题效率。这种方法很可能体现在压轴题的分步设计上,通过多个小问题逐步引导考生分析问题、寻找解题思路,最终解决复杂问题。
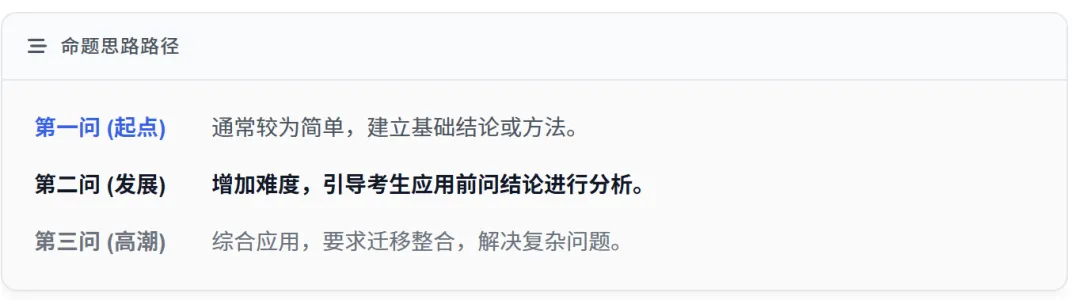
这种命题思路与江西近年中考数学真题的结构高度吻合:压轴题通常设计为2-4个小问题,难度梯度明显,第一问较为简单,第二问开始增加难度,第三问往往是综合应用,需要学生将前几问的结论或方法进行迁移或整合。

二、江西中考数学命题特色分析
1. 题型结构与难度分布
江西中考数学试卷严格遵循选择题、填空题、解答题三大模块,整体呈现"基础稳固、梯度分明、综合创新"的特征:
题型分布:选择题6题(共18分)、填空题6题(共18分)、解答题10题(共84分)。解答题占分比重较大,尤其是后几道综合题,往往成为区分度较高的题目。
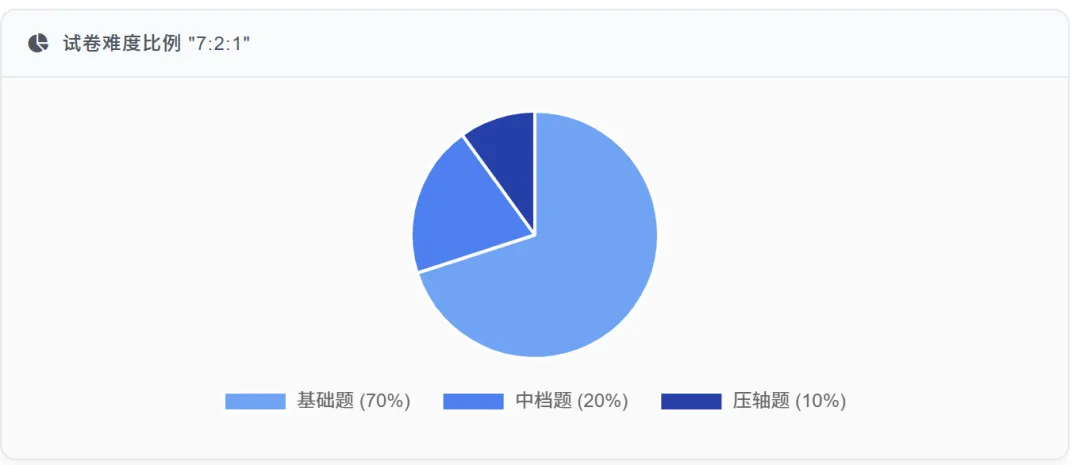
难度比例:试卷难度呈现"7:2:1"的梯度,即70%的基础题、20%的中档题和10%的压轴题。这种设计使得不同水平的考生都能在试卷中找到适合自己的题目,体现了"因材施考"的理念。
命题导向:从"知识覆盖"转向"素养导向",要求考生在掌握基础知识的同时,具备灵活运用知识解决复杂问题的能力。这一转变与黄卫民老师"以德施教与能力培养结合"的理念高度一致。

2. 压轴题的核心特点
江西中考数学压轴题通常为23-24题,具有以下鲜明特色:
综合与实践导向:近年来江西中考数学坚持将综合与实践作为必考压轴题,题目通常以特殊四边形为背景,考查几何变换、函数建模等综合应用能力。如2025年真题以正方形为背景,探究旋转放缩问题;2024年真题以菱形为背景,考查手拉手相似与解直角三角形的综合应用。
分步引导设计:压轴题通常设计为多小问,难度逐步提升,通过前几问的结论或方法为后续问题提供思路。例如2023年真题压轴题第一问通过特殊值求解,第二问通过函数关系建立,第三问通过几何变换探究,第四问通过一般化推广,形成完整的思维链条。
思维量大于计算量:题目设计注重逻辑分析而非复杂计算,考生只需通过简单的计算即可得出答案,但需要具备较强的几何直观和代数推理能力。这种设计符合"多思少算"的命题理念,强调思维过程的考查。
跨学科融合与现实情境:题目常融入物理、化学等学科知识或现实生活情境,考查学生运用数学知识解决实际问题的能力。如2024年真题中出现的物理反射原理与数学几何变换的结合题,以及2025年真题中的医保报销分段函数应用题。
新定义问题:近年来江西中考数学压轴题中常见新定义概念,如"不动点"等。这类题目考查学生对新概念的理解和应用能力,与黄卫民老师的"名称概念教学法"高度契合。



3. 典型题型与解题思路
江西中考数学压轴题常见的题型及解题思路包括:
几何变换与函数综合:如正方形、菱形的旋转、对称变换与函数图像的结合。这类题目通常需要考生通过几何变换分析图形性质,再建立函数模型进行求解。
手拉手模型与相似三角形:如2024年真题中的手拉手相似模型。这类题目通常需要考生识别基本几何模型,应用相似三角形的判定与性质进行解题。
动态几何与最值问题:如动点轨迹与函数最值的结合。这类题目通常需要考生通过动态分析,找到几何关系中的不变量,建立函数模型求解最值。
新定义与应用题:如"不动点"、"推拉门闭合参数"等新定义问题,结合实际场景设计。这类题目考查学生快速理解新概念并灵活应用的能力,与黄卫民老师的"名称概念教学法"直接相关。

三、江西中考数学压轴题考查方向
1. 核心知识考查

江西中考数学压轴题主要考查以下核心知识:
几何变换:旋转、对称、平移等变换的性质与应用。如2025年真题考查正方形的旋转与放缩,2024年真题考查菱形的旋转与相似。
相似三角形与全等三角形:相似与全等的判定与性质,以及在几何问题中的应用。如2024年真题通过相似三角形探究线段比例关系。
二次函数与几何综合:二次函数的图像与性质,以及与几何问题的综合应用。如2023年真题通过二次函数建立动点轨迹模型。
圆与直线形的综合:圆的基本性质,以及与三角形、四边形等直线形的综合应用。如2023年真题考查圆的切线判定与三角函数的综合应用。
新定义概念:通过题干给出新定义,考查学生理解与应用能力。如2025年真题中的"不动点"定义,需要学生通过名称理解其数学含义。

2. 核心素养考查
江西中考数学压轴题不仅考查基础知识,更注重以下核心素养的考查:
数学抽象:从具体问题中抽象出数学模型的能力。如通过现实场景(医保报销、新能源汽车)抽象出分段函数模型。
逻辑推理:通过已知条件推导未知结论的能力。压轴题通常需要考生通过严谨的逻辑推理,逐步解决复杂问题。
数学建模:将实际问题转化为数学问题并求解的能力。如通过物理反射原理建立几何模型,或通过经济问题建立方程模型。
直观想象:通过图形直观理解数学关系并进行想象的能力。几何变换类题目特别注重这一素养的考查。
数学运算:通过数学运算解决问题的能力。但江西中考数学更注重思维过程而非单纯计算,因此运算量相对较小。

四、2026年江西中考数学命题趋势预测
1. 命题团队与命题思路变化
根据江西省教育考试院发布的最新政策,2026年江西中考命题将首次引入高中教师参与,这为命题工作注入了新的活力和视角。结合黄卫民老师作为高中数学特级教师的身份和教学理念,可以预测2026年江西中考数学命题将呈现以下特点:
高中知识渗透:命题可能融入更多高中数学思维方法,如函数与方程思想、数形结合思想等,为高中数学学习做好铺垫。
命题视角提升:高中教师参与命题,可能使题目设计更加系统、严谨,注重数学知识的内在联系和逻辑推理。
命题风格融合:黄卫民老师的"名称概念教学法"和"庖丁解牛解题法"很可能与高中教师的命题风格相融合,形成更加注重思维过程和能力迁移的命题特色。


2. 压轴题命题方向预测
结合黄卫民老师的教学理念、近年江西中考数学真题分析以及2026年中考改革方向,可以预测2026年江西中考数学压轴题可能考查以下方向:
几何变换与函数综合:以特殊四边形(如正方形、矩形、菱形)为背景,考查旋转、对称等几何变换与二次函数、一次函数的综合应用。题目可能通过多小问逐步引导考生从特殊到一般地探究几何变换的性质与函数关系。
新定义问题:可能设计一个新数学概念,通过简明扼要的名称和定义引导考生理解其数学含义,再通过具体问题考查考生的应用能力。这种设计与黄卫民老师的"名称概念教学法"高度契合,有助于考查学生的即时学习能力和应用能力。
跨学科融合:可能融入更多学科知识和现实生活情境,如物理中的力学原理、化学中的反应速率、经济中的成本效益分析等,考查学生运用数学知识解决实际问题的能力。
代数推理强化:由于高中教师参与命题,代数推理能力的考查可能得到加强,如通过方程、不等式、函数等代数工具解决几何问题,体现数学知识的内在联系和综合应用。
开放性探究题:可能设计更具开放性的探究题,要求考生通过尝试、猜想、验证等步骤解决问题,考查学生的探究能力和创新意识。

3. 备考策略建议
基于对黄卫民老师命题思路和江西中考数学命题趋势的分析,针对2026年江西中考数学备考,提出以下建议:
重视基础概念理解:黄卫民老师的"名称概念教学法"强调从概念名称理解数学本质。因此,考生应重视对数学概念本质的理解,而非单纯记忆解题步骤。
培养问题拆解能力:针对"庖丁解牛解题法",考生应培养将复杂问题拆解为简单步骤的能力,通过多练习综合性题目,提升分析问题和解决问题的能力。
强化几何直观与代数推理:江西中考数学压轴题注重几何直观和代数推理能力的考查。考生应加强几何变换、相似三角形、二次函数等核心知识的学习,同时注重代数方法在几何问题中的应用。
关注新定义问题:考生应熟悉新定义题型的解题思路,通过名称理解概念本质,再通过具体例子验证理解,最终解决相关问题。
注重思维过程训练:江西中考数学命题注重思维过程而非单纯计算。考生应重视解题过程的规范性和严谨性,培养良好的数学思维习惯。

五、黄卫民命题特色与近年真题关联分析
通过分析近年江西中考数学真题,可以发现其与黄卫民老师的教学理念和方法高度契合,具体表现在以下几个方面:

1. 概念名称解析的体现
2025年江西中考数学第21题"函数新定义问题",考查"不动点"这一新概念。题目通过"根据定义可知不动点横纵坐标相等"的提示,引导考生从名称理解概念本质,即函数图像上横纵坐标相等的点。这种命题思路与黄卫民老师的"名称概念教学法"完全一致。
2023年江西中考数学第6题"七巧板拼接成轴对称图形",考查轴对称图形的定义。题目通过"轴对称图形"这一名称,引导考生理解其数学含义,即在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。这种从名称理解概念的命题思路,符合黄卫民老师的教学理念。

2. 庖丁解牛解题法的体现
2024年江西中考数学第23题"综合与实践压轴题",以菱形为背景,考查三角形的旋转放缩问题。题目设计为四个小问题:

(1)当m=1时,求线段比例;
(2)将三角形绕点A逆时针旋转并放大,求线段比例;

(3)猜想线段比例是否与旋转角有关;
(4)探究线段间的数量关系。
“庖丁解牛”式题目分解 (2024年真题)
第(1)问: 建立基础,通过已知条件求解线段比例。
第(2)问: 引入变量,将问题一般化,求解新条件下的线段比例。
第(3)问: 引导猜想,探究线段比例与旋转角的内在关系。
第(4)问: 综合应用,探究线段间的数量关系,完成证明。
这种分步引导、逐步深入的设计,与黄卫民老师的"庖丁解牛解题法"高度一致。考生需要从简单情形入手,通过几何变换分析图形性质,再逐步推广到一般情况,最终解决复杂问题。题目通过前几问的结论或方法为后续问题提供思路,体现了命题者对解题过程的引导和对思维过程的考查。
2023年江西中考数学第24题"动态几何与函数综合",考查推拉门闭合问题。题目设计为三个小问题:

(1)求CMN的面积;
(2)探究面积随角度变化的规律;
(3)求面积的最大值。
同样体现了分步引导、逐步深入的设计,考生需要从静态图形入手,逐步分析动态变化过程,建立函数模型,最终解决最值问题。这种设计符合黄卫民老师"将复杂数学问题拆解为可操作的步骤"的教学理念。

3. 跨学科融合的体现
2024年江西中考数学真题中,出现了一道将物理反射原理与数学几何变换相结合的题目。题目通过"光的反射"这一物理现象,构建数学模型,考查几何变换和函数关系。这种跨学科融合的设计,与黄卫民老师"注重从身体、习惯、品行着手"的育人理念相呼应,体现了数学知识在现实生活中的广泛应用。
2025年江西中考数学真题中,出现了一道以"医保报销"为背景的应用题,考查分段函数模型的建立与应用。题目通过现实生活中的医保报销政策,构建数学模型,考查考生运用数学知识解决实际问题的能力。这种设计符合黄卫民老师"将德育贯穿教学全过程"的理念,体现了数学教育的社会价值。

六、总结与展望
黄卫民老师作为江西省特级教师、教育部名师培养对象,很可能参与了2026年江西中考数学命题工作。他的"名称概念教学法"和"庖丁解牛解题法"两大原创教学方法,很可能成为其命题设计的核心方法论。
江西中考数学命题呈现"基础稳固、梯度分明、综合创新"的特征,压轴题注重思维过程而非单纯计算,强调几何直观和代数推理能力的考查。这种命题风格与黄卫民老师的教学理念高度契合,即重视基础知识的掌握,同时注重能力培养和思维训练。
2026年江西中考数学命题趋势主要体现在以下几个方面:
高中教师参与命题:命题团队将首次引入高中教师,可能使题目设计更加系统、严谨,注重数学知识的内在联系和逻辑推理。
思维导向强化:命题将继续强调思维过程而非单纯计算,注重几何直观、逻辑推理、数学建模等核心素养的考查。
跨学科融合深化:题目可能融入更多学科知识和现实生活情境,考查学生运用数学知识解决实际问题的能力。
代数推理能力提升:由于高中教师参与命题,代数推理能力的考查可能得到加强,如通过方程、不等式、函数等代数工具解决几何问题。
新定义问题创新:命题可能设计更具创新性的新定义问题,通过名称理解概念本质,再通过具体例子验证理解,最终解决相关问题。
对于考生而言,备考时应注重基础概念的理解,培养问题拆解能力,强化几何直观与代数推理,关注新定义问题,注重思维过程训练。通过系统复习教材内容,多练习综合性题目,提升分析问题和解决问题的能力,才能在2026年江西中考数学中取得优异成绩。
黄卫民老师的命题思路和方法,不仅体现了他对数学教育的深刻理解,也反映了江西中考数学命题的改革方向。随着高中教师参与命题,江西中考数学将更加注重思维过程和能力迁移,为培养具有创新精神和实践能力的数学人才做出更大贡献。这种改革方向与黄卫民老师的教学理念不谋而合,预示着未来江西中考数学命题将更加科学、严谨、富有创新性。

最终展望 (FINAL OUTLOOK)
随着高中教师参与命题,江西中考数学将更加注重思维过程和能力迁移,为培养具有创新精神和实践能力的数学人才做出更大贡献。








