【2025中考最值问题7】【浙江24(2)②】【求线段差的最小值】

试题内容

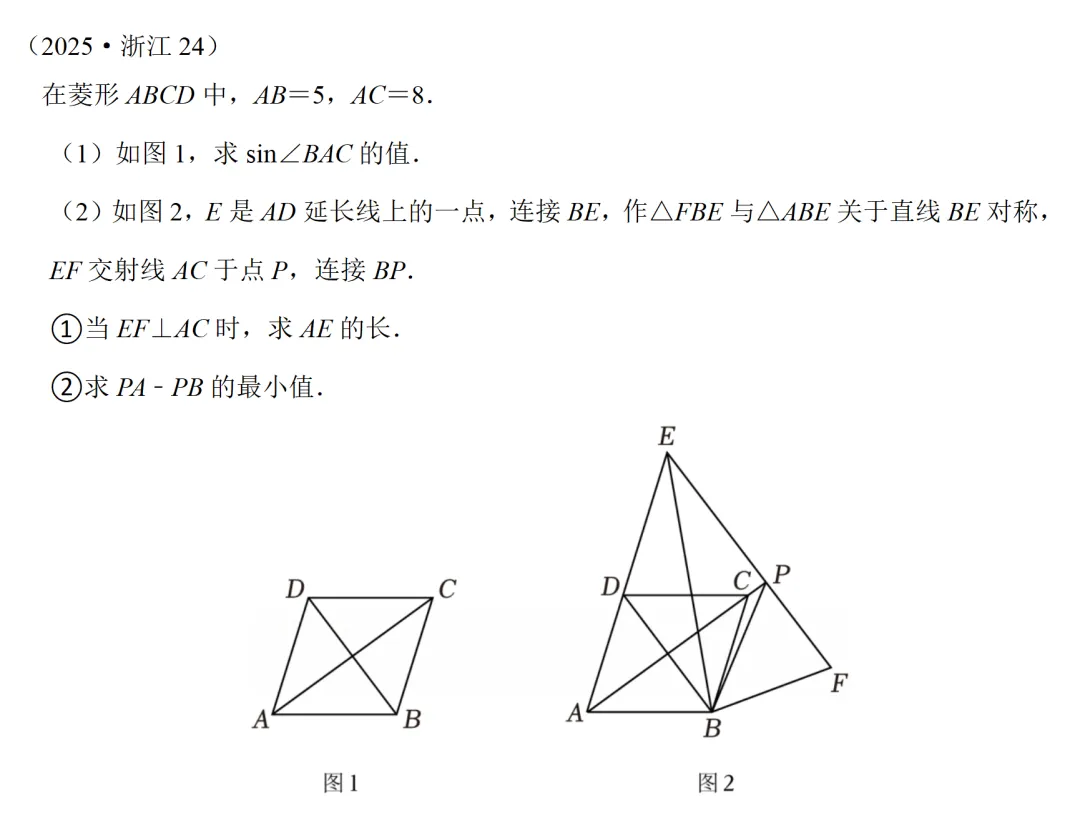
解法分析(2)②

准备工作

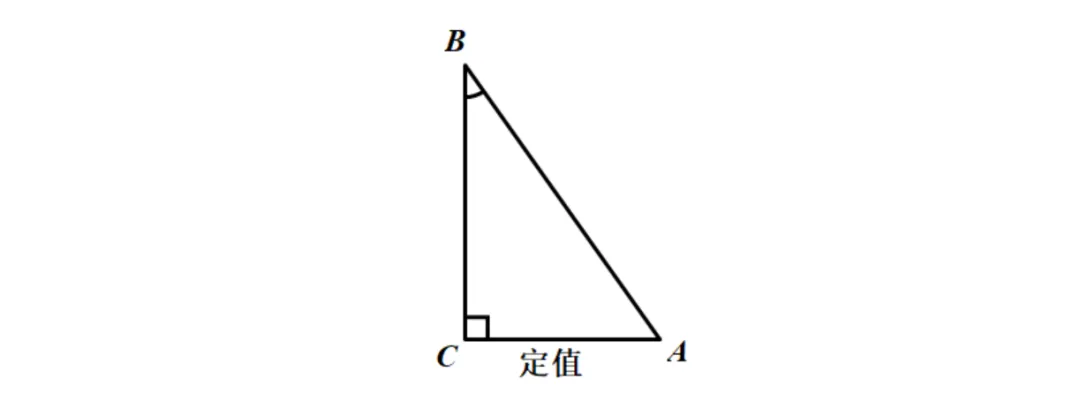
在直角三角形ABC中，直角边AC的长为定值.∵BC·tanB=定值，AB·sinB=定值，∴BC、AB随∠B的增大而减小.（结论①）∵AB=定值+BC，∴AB随BC的增大而增大.（结论②）

方法1：在长线段上截取短线段，求线段差的最小值.

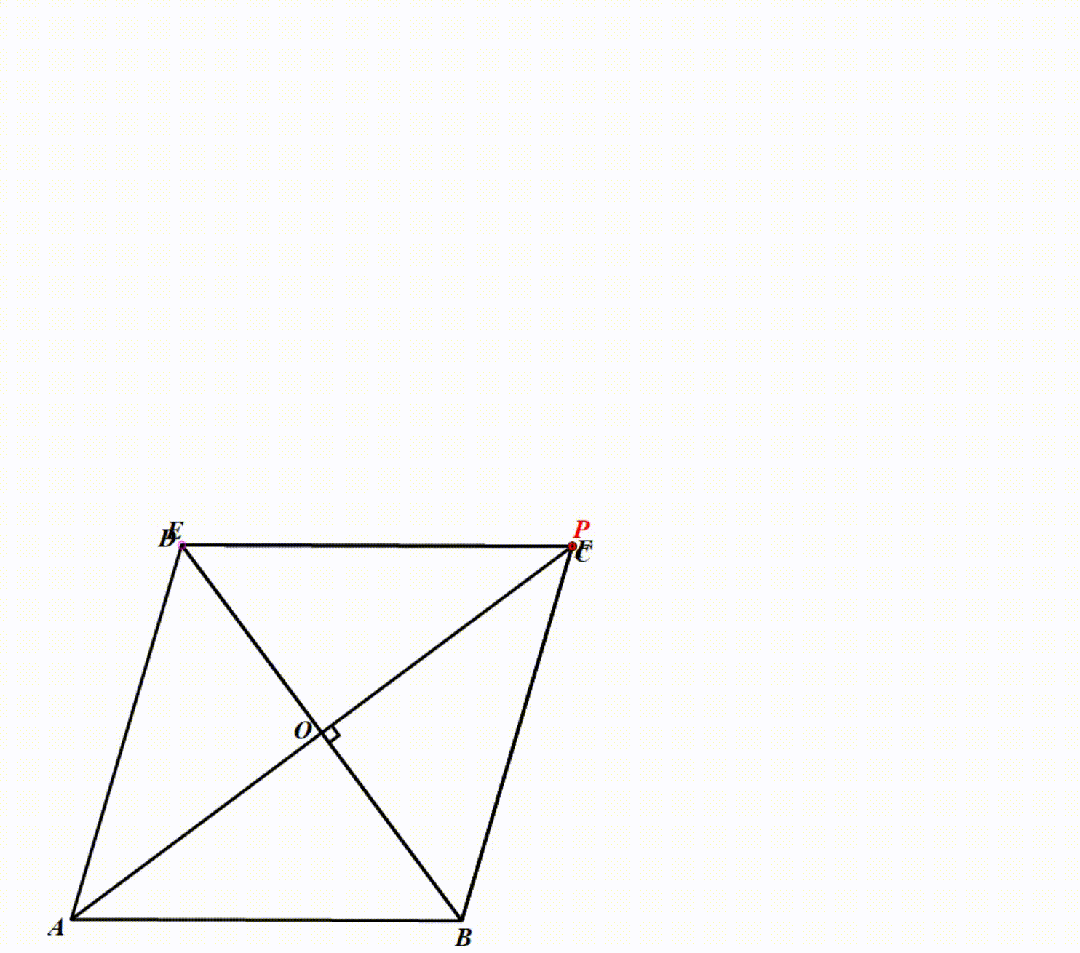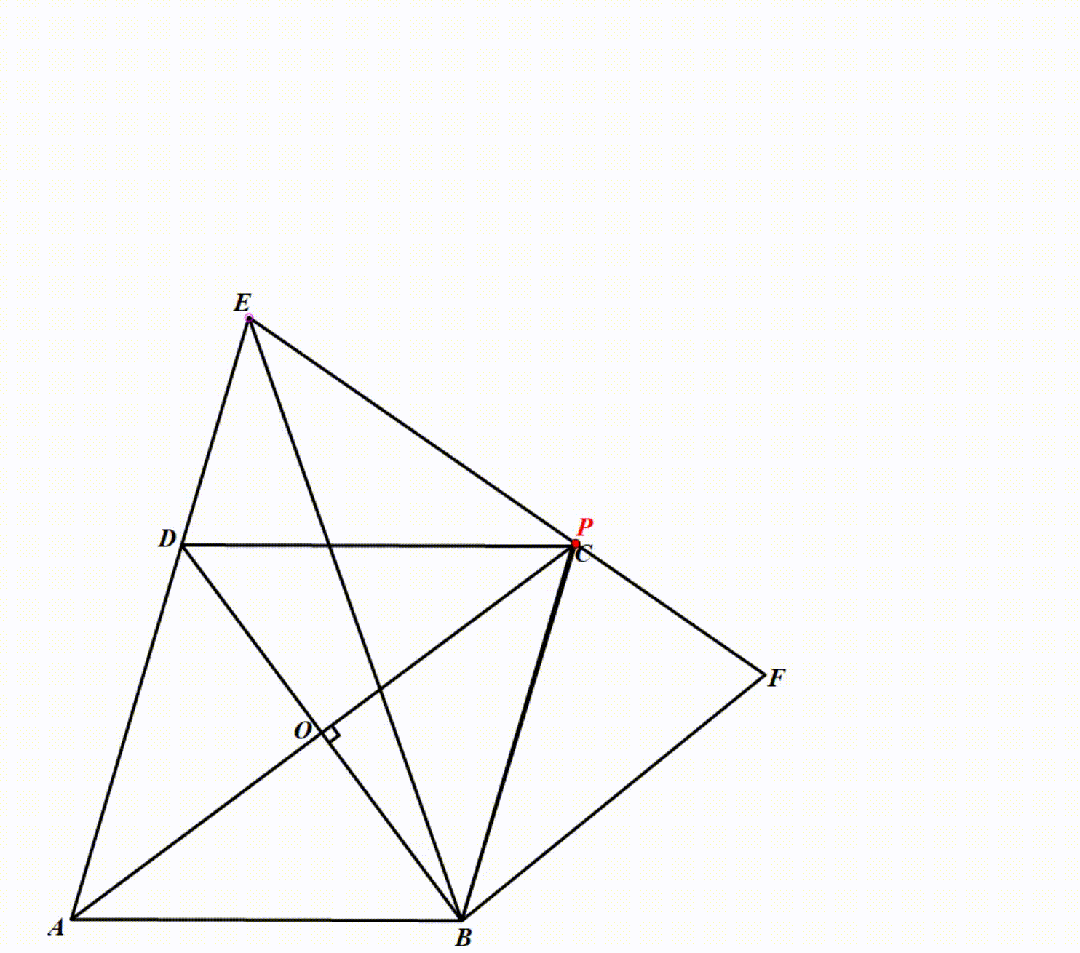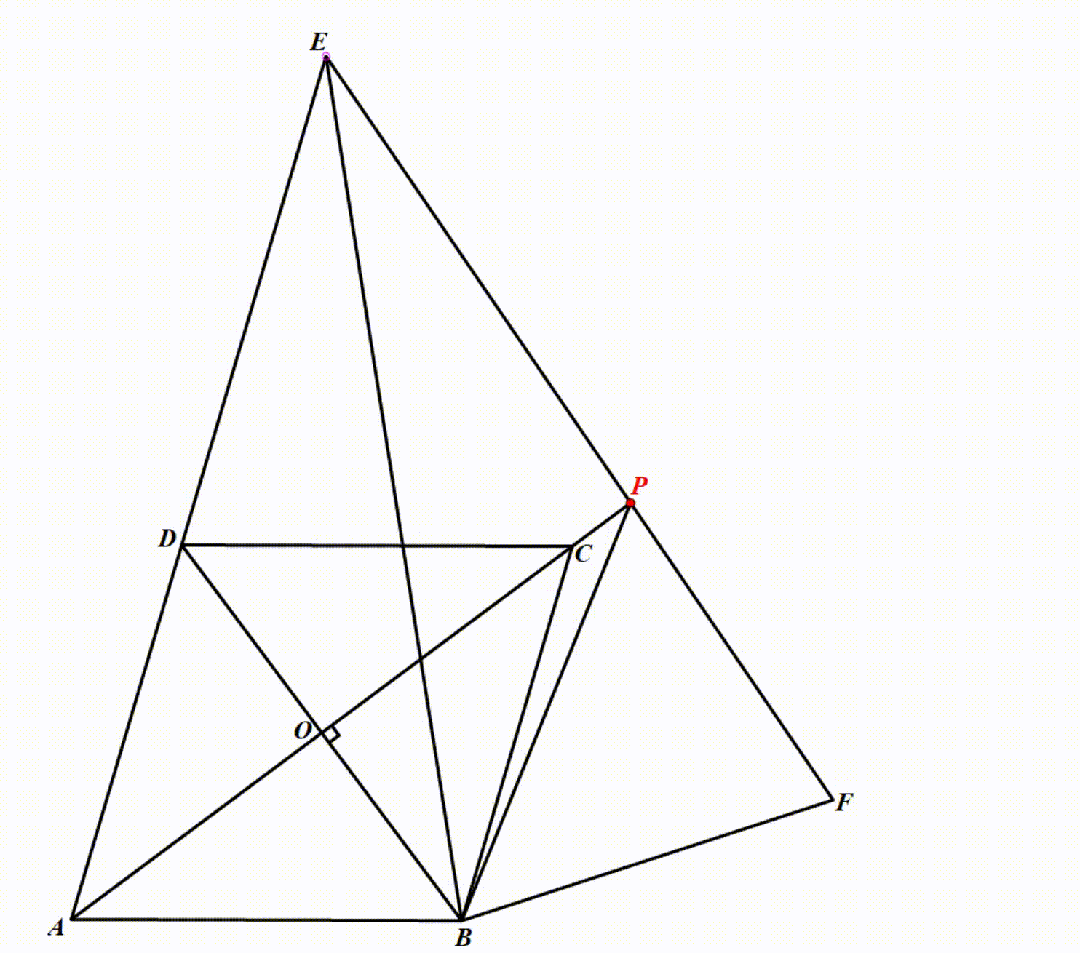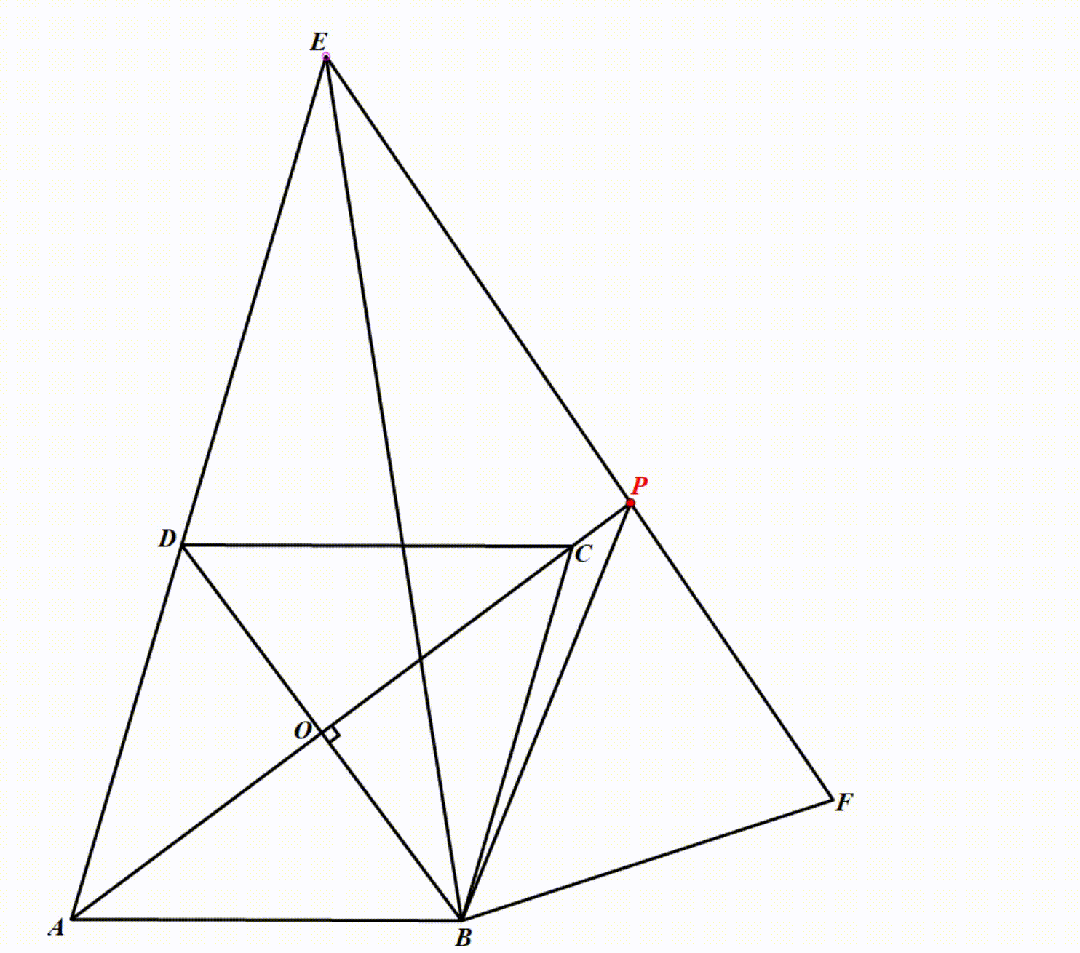
如左图，在PA上截取PG=PB，则AG=PA-PB.∵PG=PB>PO，∴点G在AO上.问题可进行如下转化：PA-PB最小→AG最小→OG最大→∠OGB最小（结论①） →∠BPG最大→PB最小（结论①）→PB⊥EF.

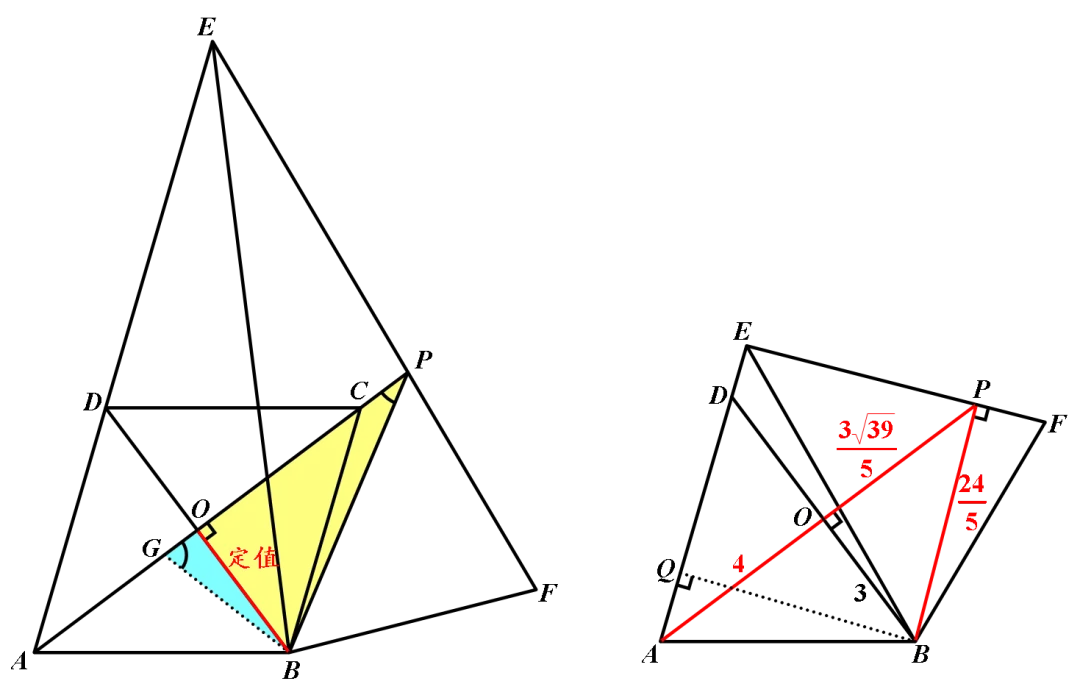
如右图，作BQ⊥AE于点Q，易证：QB=PB，BD=6，∴QB==，∴PB=.由勾股定理得：OP=.∴(PA-PB)=4+-=.

方法2：勾股定理→平方差公式→化线段差为线段和.

如左图，PA-PB=OA+OP-PB=4-(PB-OP).由勾股定理得：PB-OP=9，∴PB-OP=.问题可进行如下转化：PA-PB最小→PB-OP最大→PB+OP最小 →PB最小（结论②）→PB⊥EF.

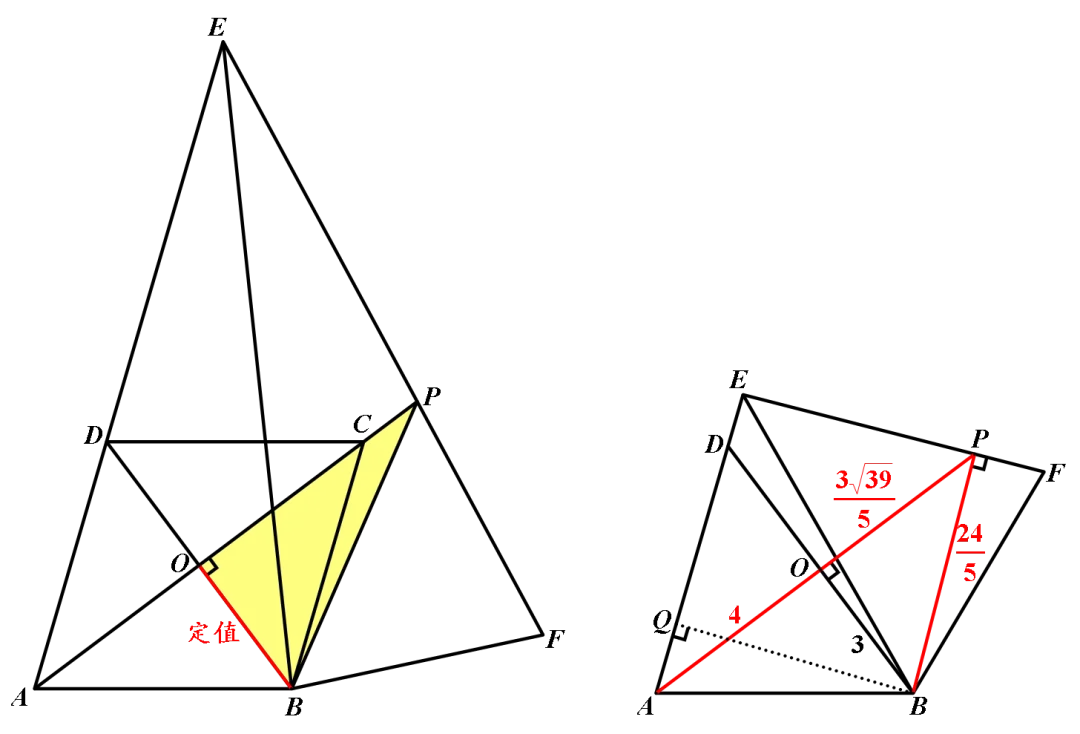
如右图，与方法1同理可得：∴(PA-PB)=.

方法3：函数模型解几何问题

如左图，设PB为，则OP=，∴PA-PB=4+-=4-.（分子有理化）当取最小值时，PA-PB最小.

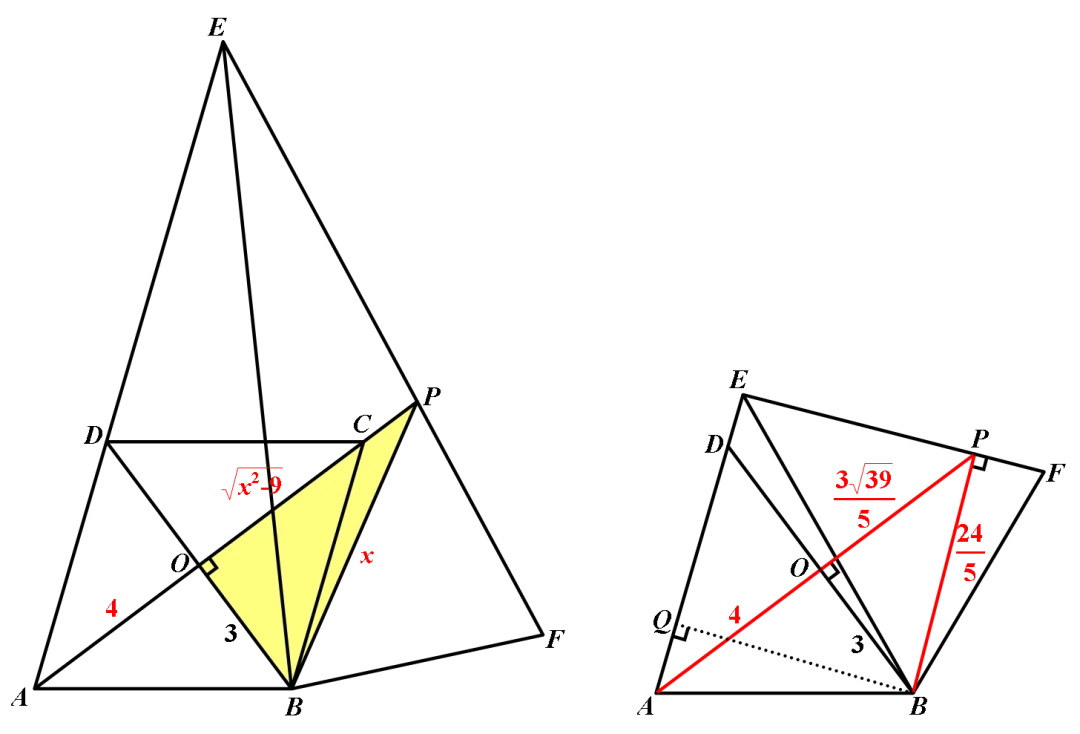
如右图，与方法1同理可得：∴(PA-PB)=.

动态演示