


试卷基本情况
1.
试卷的结构、题型及分值比例
2025年福建省中考数学试卷合理设置试卷结构和难度结构,科学取样,较为全面地检测学生的基础知识与学科素养。
从题型题量看,试卷涵盖选择题、填空题和解答题,其中选择题 10道占 40 分;填空题6道,占24分;解题9道,18道小题,占86分。
从知识分布看,数与代数共54分,占比36%;图形与几何共64分占比42.67%;统计与概率共16分,占比10.67%;综合与实践共16分占比 10.67%。知识分布与课标规定的内容占比基本一致(见表1)。

从目标要求看,涉及了解的知识有28分,占比18.67%;涉及理解的知识有 34分,占比22.67%;涉及掌握的知识有86分,占比57.33%;涉及运用的知识有29分,占比19.33%,符合学业水平考试定位(见表2)。

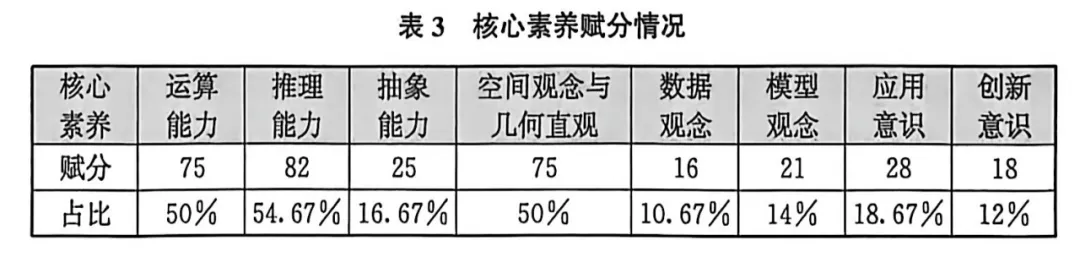
从核心素养看,全面覆盖了义务教育数学课程标准要求的九大核心素养表现,其中运算能力75分,占比50%;推理能力82分,占比54.67%抽象能力 25分,占比16.67%;空间观念与几何直观75分,占比50%;数据观念 16 分,占比10.67%;模型观念21分,占比14%;应用意识28分占比18.67%;创新意识18分,占比12%,较好地体现了素养导向下的能力立意的命题要求(见表3)。
2.
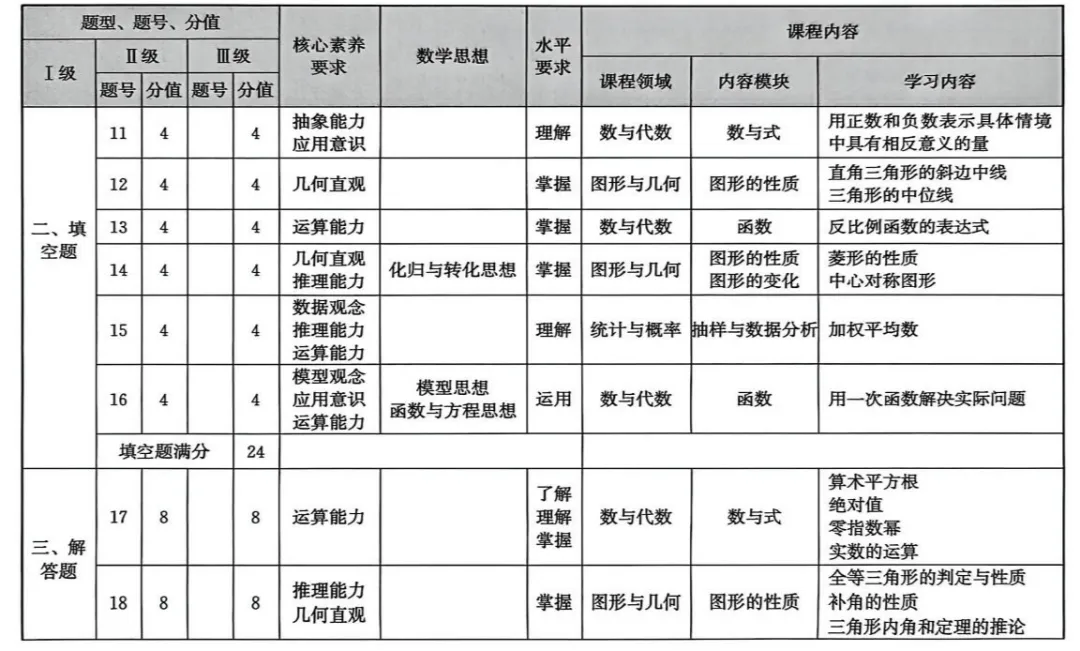
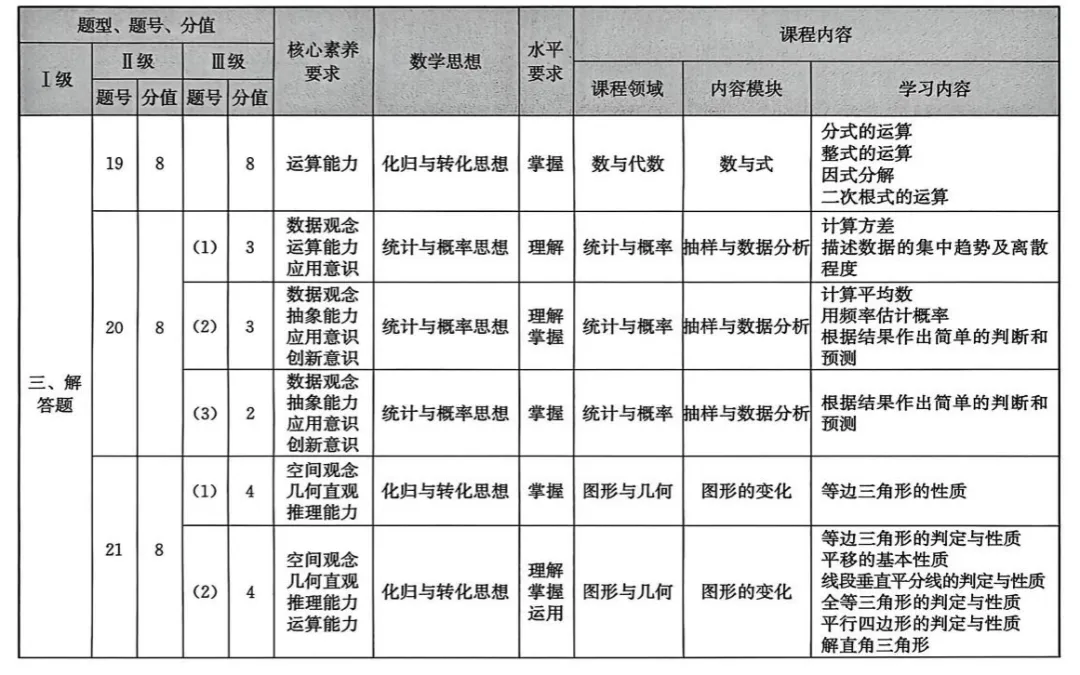
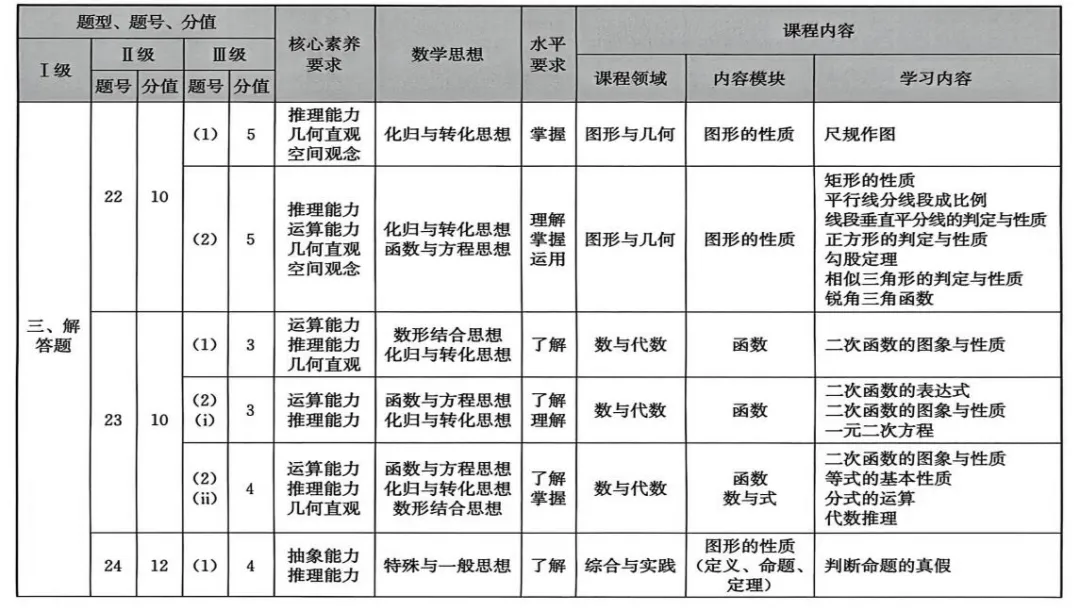
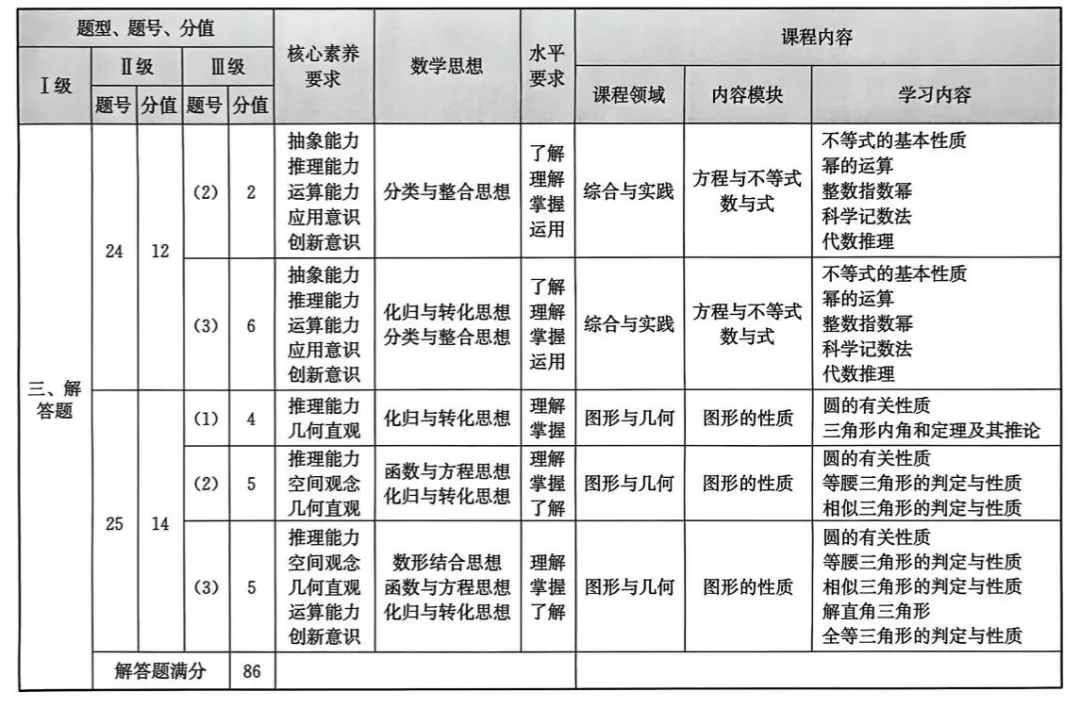
试卷考查内容分布表

3.
试卷特色
(1)关注情境创设,落实学科育人
2025年福建省中考数学试卷关注情境创设,合理设置问题情境,自然融入数学文化、学校生活、国计民生、生活实践等问题,着力五育并举倡导全面发展,体现正确的价值引领。全卷共25题,情境内容丰富,形式多样,既有生活情境、社会情境、科学情境,也有数学情境,其中涉及生活、社会和科学情境的题目就有 10题,数量占比合理,符合课程标准要求,这些题目较好地考查了学生问题的分析与解决、信息的获取与处理、数学建模等各种能力,寓思想教育于试题之中,有效落实“四能”,发展“三会”,实现学科育人。
例如,第2题以中国古算诗词题为背景,弘扬中华优秀传统文化,体现文化自信;第4题以福建博物院藏品——云纹青铜大铙为背景,引导学生感受家乡的渊源历史与灿烂文化,激发学生爱国爱乡的家国情怀;第8题以建设劳动实践基地为背景,体现劳动教育;第11题以2025年为“体重管理年”为背景,融入体育教育,引导学生关注社会、关注生活,同时融入数学抽象,要求学生学会“用数学的语言表达现实世界”;第2题古算诗词题中表述的对称图形、第4题云纹青铜大铙抽象出的立体图形、第12题中的房梁结构等,都体现了数学的对称美、和谐美和简洁美,让学生在解决问题的过程中,接受美学熏陶。
理性思维水平和分析、解决问题的能力是数学学科对智育考查的重要内容,2025年福建省中考数学试卷对学生理性思维水平和分析、解决问题能力的考查深入、具体、到位。例如,第21题以等边三角形和平行四边形为构图背景,分步设问,逐步推进,考查由浅入深,层次分明,重点突出内容丰富。在问题解决过程中,知识掌握的牢固程度、运算求解的娴熟程度、逻辑推理的敏捷性与严密性都得到充分的体现;第15题既可以通过计算加权平均数得到答案,也可以在深刻理解加权平均数概念的基础上,通过观察、对比数据的变化,直接作出判断,不同的方法彰显数学思维能力的不同层次,深刻考查了理性思维的深广度。
(2)聚焦核心素养,关注学习潜能
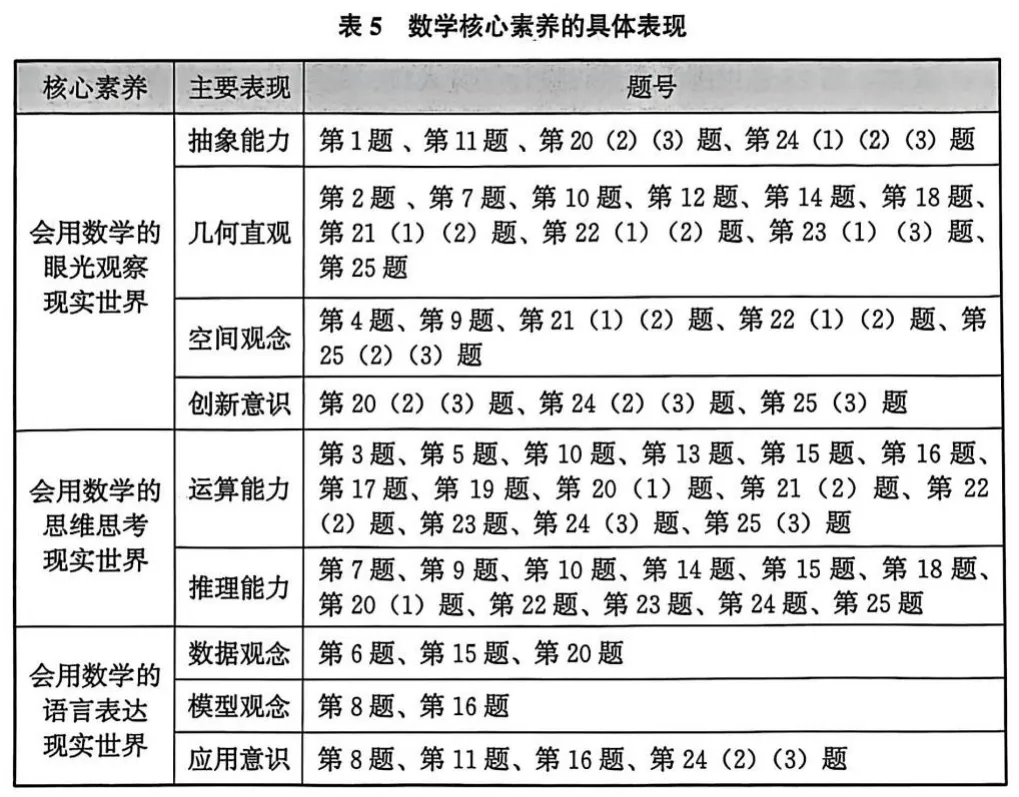
2025年福建省中考数学试卷聚焦核心素养,立足“四基”“四能”,围绕“三会”目标的具体表现,如抽象能力、运算能力、推理能力、几何直观、空间观念、数据观念、模型观念、应用意识、创新意识等,全面检测数学学科核心素养和关键能力的达成度。试题设计注重在问题情境中考查学生数学核心素养的发展水平,特别是通过开放性任务和探究性问题,有效诊断学生的思维品质、关键能力和学习潜能,充分体现了数学学科独特的育人价值(见表5)。
值得一提的是,“综合与实践”作为初中数学四个学习领域之一,是学生积累数学活动经验、培养应用意识和创新意识的有效载体,也是考查学生思维品质和学习潜能的有效载体。例如,第24题设置“背景材料十问题任务”的情境,将抽象的概念、法则、命题置于人文情境与数学情境之中,层层递进地构建问题,研究内容逐步深入,并通过情境搭建试题框架,借助小华的探究过程设计问题。问题的呈现是考生没有接触过的“新”的数学知识和规律,问题的解决需要通过阅读文本、获取信息、处理信息、建立模型等,特别是在“推广延伸”环节中更需要通过阅读,充分理解相关概念,读懂代数推理过程,理解每一步推理的算理、算法,通过积极的反思与质疑,才能理解所建构的新知识及新方法,进而建立不等式(组)型,运用已有的认知经验解决问题。“问题 3”更是需要考生用数学语言表达“迁移拓展”的结论,引导学生用规范的数学语言表达推理与论证过程实现对分析、推理、判断等代数领域关键能力的考查。解决问题所经历的发现规律、表达规律、证明规律、应用规律的研究路径,正是科学研究的基本路径之一,较好地考查了学生进一步学习的潜能。
又如,第 25 题以圆为背景,设计了宽入口、低起点、高落点的三个层层递进的问题,既考查了平面几何的主干知识,又考查了化归与转化思想、数形结合思想;既关注合情推理能力和演绎推理能力,又关注数学活动经验的积累和运用,要求学生用数学的眼光去发现问题,在解决问题的过程中归纳方法、提炼思想,尝试从不同角度、用不同方法解决问题,较好地考查了学生的学习潜能。
(3)强调学科思维,突出数学本质
2025 年福建省中考数学试卷立足初中数学四个知识领域的教育价值:“数与代数”领域通过符号化表达与结构化思维,培育抽象能力、运算能力、代数推理及模型观念,在数学严谨性中养成科学精神;“图形与几何”领域依托直观感知与空间想象,系统培养几何直观、空间观念及推理能力,建立从直观到抽象的数学认知路径;“统计与概率”领域聚焦数据批判思维与随机观念培养,强调基于数据的科学决策能力,形成数据驱动的现代社会素养;“综合与实践”领域整合跨领域知识解决真实问题,重点发展创新应用能力与数学建模思想。试卷以“情境真实性、思维层次性、方法多样性”为特色,通过开放探究、综合与实践等题型,引导学生在理解数学本质的过程中发展批判性思维,形成严谨求实的科学精神,最终实现从注重知识回忆到注重思维过程,从知识掌握到素养提升的跨越式发展。
例如,第 20题通过创设实际问题情境,考查学生对统计量含义的理解。问题的解决需要通过对数据的系统分析,并根据题目的具体要求及统计量的实际含义作出决策,从中感悟统计思维与思想方法,培养数据分析观念,在理解统计本质的基础上发展批判性思维。
第22题以尺规作图为载体,综合考查了几何与代数的相关知识、思想方法的灵活应用以及核心素养的多重表现。第(1)问需执果索因,通过逻辑推理寻找作图的切入点,经历“推理探索一尝试操作一论证证实”等过程,感悟尺规作图的合理性,强化学生对几何元素之间关系的直观理解,感受图形形成过程中的数学思维生成,突出数学本质;第(2)问需先利用图形的中心对称性直观判定正方形的中心是矩形对角线的中点,再利用平行线分线段成比例加以证明,并根据相似三角形的判定与性质或锐角三角函数求解,促进数学思维发展。
第23题以二次函数为载体,聚焦运算能力、推理能力、几何直观和空间观念等核心素养,综合考查“以形助数”的直观感知能力,根据概念、公式、法则等进行恒等变形的代数运算能力,根据运算结果进行“以数解形”的演绎推理能力。第(2)(i)问以二次函数最大值条件作为切入点,既可代入解析式求解,也可通过配方等方法求解;第(2)(ii)问关注目标导向下的代数式恒等变形,选择恰当的变形策略,确保变形得当,对解决问题至关重要。解题过程凸显思维的条理性和逻辑性。
第25题以圆为载体,聚焦推理能力、空间观念、几何直观和运算能力等核心素养,解决问题需要具备清晰的逻辑推理能力,深入研究由基本图形衍生出新的几何图形,通过正确构图、识图,分析图形中的基本元素及其相互关系,作出定性判断和定量计算。在此过程中借助数形结合揭示问题的数学本质,并运用已有的认知经验进行求解。本题的解题方法多样,凸显思维的深刻性与灵活性。
(4)调整难度结构,体现考试性质
2025年福建省中考数学试卷合理设置试卷结构和难度结构,充分关注“双减”的要求,合理兼顾初中学业达标检测与高中阶段招生选拔的双重职能,在谋篇布局上合理设置基础性、综合性、应用性、创新性的试题比例,分三级难度梯度设置试卷结构,给不同水平的学生提供展现才华的空间,充分体现初中学业水平考试的考试性质。
试卷科学把握稳定与求新的辩证关系,灵活、科学地确定试题的内容、顺序和难度。例如第1-15题,第17-19题,在试题设计上,单个试题涉及的知识点相对较少、思路相对直观,充分体现了基础性。基础题的增加,除了给学生留有更多的思考时间之外,也给学生更多展示思维水平的机会。学生可以从容地思考、试错,使思维能力强的学生脱颖而出,例如第7、9题,考查基础知识和基本方法,考生既可以从图形直观感知入手,也可以从数据入手,还可以通过逻辑推理判断,满足不同层次的思维要求,适应不同思考习惯的学生。
在突出基础性考查的同时,部分试题也关注了综合性、应用性、创新性,让优秀的学生有思考的空间和发挥的余地,实现选拔功能。例如,第16 题以弹簧秤为载体,根据弹簧秤工作原理所蕴含的数学知识和物理知识,抽象出数学模型,通过建立一次函数模型解决实际问题,体现了数学知识在其他学科的应用,强调学以致用。又如,第24题要求利用初中学过的代数知识来证明小学所学的多位数乘法的有关结论。问题的解决需要通过对题文的阅读把握题意,并在领会题意的基础上借助特例探索发现规律,再利用代数知识对规律的正确性进行论证,进而拓展迁移。第(3)问既可以借助阅读小华的证明过程所积累的经验,利用小华的方法解决;也可以直接利用小华的命题结论作为依据解决问题,较好地考查了创新意识和创新思维。
试卷机动调整题目顺序,灵活确定试题的考查内容,打破机械应试的套路模式,引领课堂教学改变僵化、固定的训练模式,引导全面落实国家课程标准。例如,第 24题以“位数探究”为载体,设置了综合与实践试题,重点考查代数推理能力,改变了前两年以几何为背景的综合与实践试题的风格;第 23题回归考查二次函数的图象与性质;第 22题的尺规作图题设置以矩形中求作正方形的推理型作图,其本质为圆中作正方形,区别于2024年以直线型为背景的作图:第21题回归以图形变换为背景,考图形的判定与性质。
(5)立足课程标准,引导回归教材
2025年福建省中考数学试卷遵循课标要求,严格依标命题,许多试题来源于教材中的例题、习题,依托变更问题情境、改变题设数据、更改设问类型等方式对原题合理改编。
第15题来源于我省使用的三个不同版本教材的共有素材,通过改变条件和结论,从不同的视角设问,考查学生对“权”的理解。只要全面落实国家课程标准,掌握加权平均数的计算方法,便可通过计算得到答案;如果学生深刻理解“权”的含义,也可通过观察对比数据的特征,直接作出判断。给不同思维水平的学生提供不同的发挥空间,体现了“源于教材,高于教材”的命题思路。
第 24 题的综合与实践问题以数学活动为载体,以发现数学规律为要旨,其设计思路来源于 2011版课标的案例 27“‘数的大小’的传递与缩放”和2022 版课标的案例6“根据大小关系排序”,深刻考查了不等式的基本性质、科学记数法和代数推理,虽然涉及的知识不多,但有效检测了学生获取信息、加工信息,综合应用相关知识分析、解决问题的能力。解决问题需要遵循数学探索发现的逻辑规律,学会像数学家一样去思考。
此外,第3、5、6、7、8、12、14、18、19 等题都有教材例习题的影子,都是教材例习题的适当改编,意在引导教学重视对教材的挖掘及合理使用,避免机械记忆和盲目刷题。
(声明:文章来源:《2026福建中考报告》。“诗仙数学”微信公众号刊载此文,是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益,请及时与我们联系,我们将及时更正、删除或依法处理。如有转载请注明出处。)

往期推荐 ●●
// 1
// 2
// 3
// 4






