中考数学热点解析(五)几何压轴题(55)

(55) 2024年凉山州中考数学第27题

如图⑴， AB 是⊙O的直径，点C 在

⊙O 上， AD平分∠BAC交⊙O于点D，

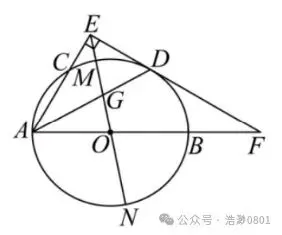
                         图⑴

过点 D 的直线 DE⊥AC 交 AC 的延长线

于点 E ，交 AB 的延长线于点 F ，

(1）求证： EF 是 ⊙O 的切线：

(2）连接 EO 并延长，分别交 ⊙O 于 M , N 两点，交 AD 于点 G ，若 ⊙O 的半径为2,∠F =30º，求 GM·GN 的值.

解析：⑴：如图⑵，连接 OD ,

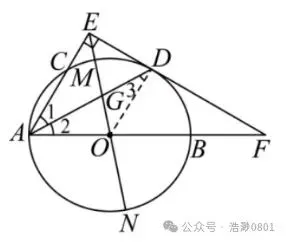
                      图⑵

∵0A= OD ,

∴∠2=∠3，

 ∵AD 平分∠BAC ，

∴∠1=∠2，

∴∠1=∠3,

∴OD // AC ,

∴∠ODF =∠AED ，

∵DE⊥AC ，

∴∠AED =90°，

∴∠ODF =90°,

即 OD⊥EF ，

 ∵OD 是 OO 的半径，

∴ EF 是 OO 的切线.

⑵：如图⑶，连接 MD , AN ,

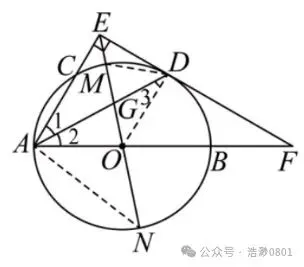
                    图⑶

∵∠F=30°,

∴在 Rt△ODF中， OF=2OD=4,

由勾股定理得

      DF=√OF²-OD²=2√3

∴AF =AO+FO=2+4=6,

∵在 RtAEF中， ∠F =30°,

∴AE =1/2AF=3,

∵∠F =30°, OD⊥EF 

∴ ∠DOF =60°=∠2+∠3，

又∵＜2=<3

∴∠2=30°,

∴∠2= LF ，

∴AD=DF=2√3,

∵OD // AE ，

∴ △DGO∽△AGE ，

∴DG/AG=OD/AE=2/3，

∴ DG =2/5AD .AG=3/5AD，

∵ ∠ANG = ∠MDG ，

     ∠MGD = ∠AGN ，

∴△ MGD ~∆ AGN ，

∴MG/AG=GD/GN

∴GM·GN = GD·GA 

          =2/5AD·3/5AD 

          =6/25AD²

          =6/25x(2√3)²

          =72/25.