
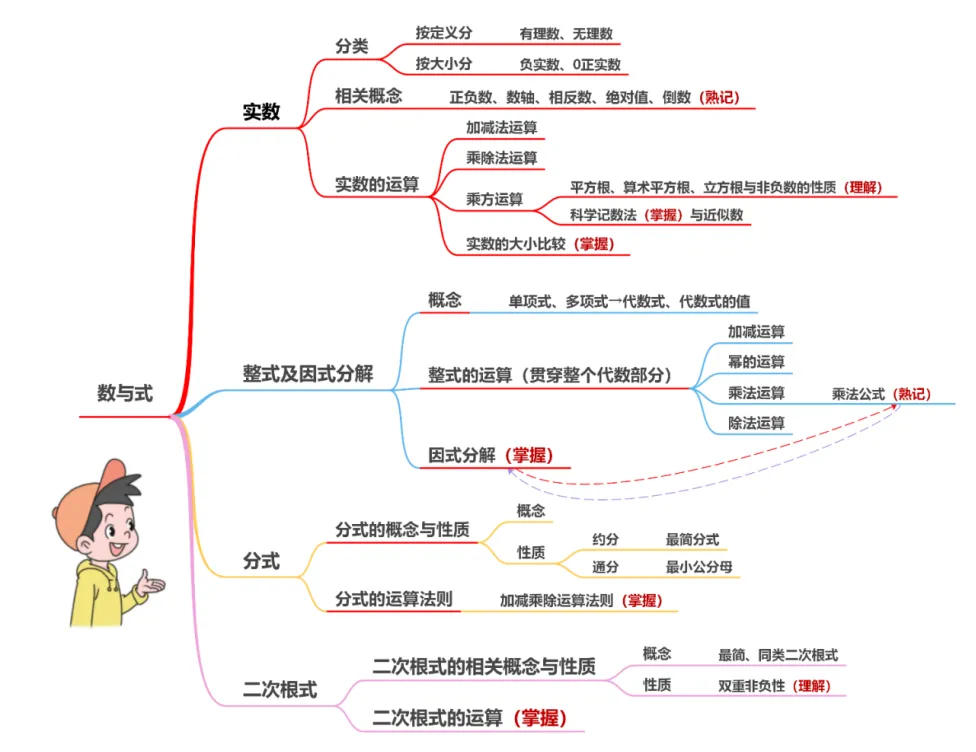

知识点 | 概念 | 补充与拓展 |
正负数 | 大于0的数叫做正数.正数前面加上符号“-”的数叫负数. | 注意:负数前面的负号“-”不能省略.0既不是正数,也不是负数. |
正负数的意义:表示具有相反意义的量.在一对具有相反意义的量中,通常先规定其中一个为正,则另一个就用负表示. | ||
数轴 | 规定了原点、正方向、单位长度的直线叫做数轴. | 数轴上的点与实数具有一一对应的关系. |
将两个数表示在同一条数轴上,右边的点表示的数总比左边的点表示的数大. | ||
在数轴上距原点n个单位长度的点有2个. | ||
数轴中点公式:数轴上有两点A、B分别表示的数为x,y,若C是A、B两点的中点,C所表示的数为c,则有:2c=x+y. | ||
数轴两点距离=数轴上右侧的点所表示的数-左侧的点表示的数(简称大数-小数). | ||
相反数 | 只有符号不同的两个数称为互为相反数. | 若a、b互为相反数,则a+b=0(反之亦成立). |
互为相反数的两个数在数轴上对应的两个点到原点的的距离相等且位于原点的两侧. | ||
正数的相反数是负数;负数的相反数是正数;0的相反数是0.相反数是本身的数是0. | ||
(a+b)的相反数是-(a+b),(a-b)的相反数是-(a-b)或b-a. | ||
多重符号化简口诀:数负号个数,奇负偶正. | ||
绝对值 | 在数轴上表示数a的点到原点的距离叫做a的绝对值,记为|a|. | 两个正数比较,绝对值大数越大;两个负数比较,绝对值大的反而小. |
正数的绝对值是它本身;0绝对值是0;负数的绝对值是它的相反数 | ||
若|a|=a(或|a|-a=0),则a≥0,若|a|=-a(或|a|+a=0),则a≤0. | ||
若a=b或a=-b,则|a|=|b|(反之亦成立). | ||
若|a|+|b|=0,则a=0且b=0(a、b可以是多项式). | ||
几何意义补充:|x|=|x-0|数轴上表示x的点到原点的距离,|x-1|数轴上表示x的点与表示1的点之间的距离,|x+2|数轴上表示x的点与表示-2的点之间的距离. | ||
倒数 | 1除以一个不等于零的实数所得的商,叫做这个数的倒数. | 0没有倒数. |
若a、b互为倒数,则ab=1 | ||
互为倒数的两个数必定同号(同为正数或同为负数). | ||
倒数是本身的只有1和-1. | ||
乘方 | n个相同的因数a相乘记作an,其中a为底数,n为指数,乘方的结果叫做幂. | 负数的奇次幂是负数,负数的偶次幂是正数 |
正数的任何次幂都是正数. | ||
规定:a0=1(a≠0) |
知识点 | 概念 | 补充与拓展 |
科学记数法 | 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数. | 用科学记数法表示数时,确定a,n的值是关键. |
当原数绝对值大于10时,写成a×10n的形式,其中1≤|a|<10,n等于原数的整数位数减1. | ||
当原数绝对值小于1时,写成a×10-n的形式,其中1≤|a|<10,n等于原数左边第一个非零的数字前的所有零的个数(包括小数点前面的零). | ||
小技巧:1万=104,1亿=1万×1万=108. | ||
近似数 | 近似数与准确数的接近程度通常用精确度来表示,近似数一般由四舍五入取得,四舍五入到哪一位,就说这个近似数精确到哪一位. | 近似数小数点后的末位数是0的,不能去掉0. |
一个近似数从左边第一位非0的数字起,到末位数字止,所有的数字都是这个数的有效数字. | ||
一个近似数有几个有效数字,就称这个近似数保留几个有效数字. |
知识点 | 概念 | 补充与拓展 |
算术 平方根 | 如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.记为,a叫做被开方数. | 正数只有一个算术平方根,且恒为正;0的算术平方根为0;负数没有算术平方根 |
平方根 | 如果一个数的平方等于a,那么这个数就叫做a的平方根或二次方根,即如果x2=a,那么x叫做a的平方根. | 正数有两个平方根,且它们互为相反数. |
0的算术平方根为0;负数没有算术平方根. | ||
立方根 | 如果一个数的立方等于a,即x3=a,那么x叫做a的立方根或三次方根. | 正数只有一个正的立方根;0的立方根是0;负数只有一个负的立方根. |
互为相反数的两个数的立方根互为相反数 | ||
实数的非负性 | 在实数范围内,正数和零统称为非负数. | 非负数有三种形式: ①任何一个实数a的绝对值是非负数,即|a|≥0; ②任何一个实数a的平方是非负数,即≥0; ③任何非负数的算术平方根是非负数,即≥0. |
非负数具有以下性质:①非负数有最小值零; ②非负数之和仍是非负数; ③几个非负数之和等于0,则每个非负数都等于0. |
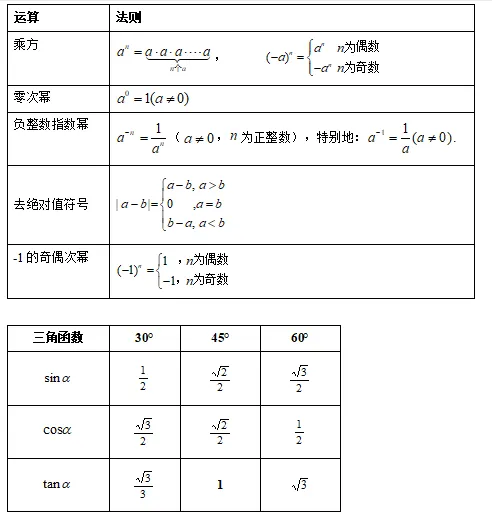
实数的四则运算法则(穿插在各个题型中)
(1)实数加法法则:
①同号两数相加,取相同的符号,并把绝对值相加;
②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.互为相反数的两个数相加得0;
③一个数同0相加,仍得这个数.
(2)实数减法法则:减去一个数,等于加这个数的相反数.
(3)实数乘法法则:
①两数相乘,同号得正,异号得负,并把绝对值相乘.任何数与0相乘,都得0;
②几个不是0的数相乘,积的符号由负因数的个数决定.当负因数的个数为奇数时,积是负数,当负因数的个数为偶数时,积是正数;
③几个数相乘,如果其中有因数为0,那么积等于0.
(4)实数除法法则:
①除以一个不等于0的数,等于乘以这个数的倒数.0不能作除数;
②两数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数,都得0.
(5)乘方的运算法则:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂都是0.
二、整式及因式分解
(一)概念
代数式、代数式的值
1.代数式的概念
用基本运算符号(加、减、乘、除、乘方、开方等)把数与字母连接而成的式子叫做代数式.单独的一个数或者一个字母也是代数式.
2.代数式的值
用具体数代替代数式中的字母,按运算顺序计算出的结果叫做代数式的值.求代数式的值分两步:第一步,代数;第二步,计算.要充分利用“整体”思想求代数式的值.
整式的有关概念(常出现在选择题、填空题)
1.整式:单项式与多项式统称为整式.
2.单项式:含有数或字母的积的代数式叫做单项式.单独的一个数或一个字母也是单项式.单项式中的数字因式叫做这个单项式的系数;一个单项式中,所有字母的指数的和叫做这个单项式的次数.
3.多项式:几个单项式的和叫做多项式.在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项.多项式里,次数最高项的次数,叫做这个多项式的次数.多项式中单项式的个数,就是这个多项式的项数.
4.同类项:所含字母相同,并且相同字母的指数也相同的项叫做同类项.几个常数项也是同类项.
5.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.合并同类项后,所得项的系数是合并前各同类项的系数的和,且字母连同它的指数不变.
因式分解(掌握):把一个多项式化成几个整式的积的形式,叫做把这个多项式因式分解.
(二)整式的运算(贯穿整个代数部分)
1.整式的加减运算:
①概念:整数的加减本质是合并同类项,如果有括号要先去括号,再合并同类项.
②去括号法则:如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
③添括号法则:添括号时,如果括号前面是正号,括到括号里的各项都不变符号;如果括号前面是负号,括到括号里的各项都改变符号.
2.幂的运算(多出选择题):
正整数幂的运算性质:

3.整式的乘除运算
整式的乘除 | 运算步骤说明 | 补充说明及注意事项 |
单项式乘单项式 | ①将单项式系数相乘作为积的系数;②相同字母的因式,利用同底数幂的乘法,作为积的一个因式;③单独出现的字母,连同它的指数,作为积的一个因式. | 1)实质:乘法的交换律和同底数幂的乘法法则的综合应用.2)单项式乘单项式所得结果仍是单项式 . |
单项式乘多项式 | ①先用单项式和多项式的每一项分别相乘;②再把所得的积相加. | 1)单项式乘多项式实质上是转化为单项式乘以单项式. 2)单项式乘多项式的结果是多项式,积的项数与原多项式的项数相同. |
多项式乘多项式 | ①先用一个多项式的每一项与另一个多项式的每一项相乘,②再把所得的积相加. | 运用法则时应注意以下两点:①相乘时,按一定的顺序进行,必须做到不重不漏; ②多项式与多项式相乘,多项式的每一项都应该带上它前面的正负号.且结果仍是多项式,在合并同类项之前,积的项数应等于原多项式的项数之积. |
单项式除单项式 | ①将单项式系数相除作为商的系数; ②相同字母的因式,利用同底数幂的除法,作为商的一个因式; ③只在被除式里含有的字母连同指数不变. | 无 |
多项式除单项式 | ①先把这个多项式的每一项除以这个单项式; ②再把所得的商相加 | 无 |
整式的混合运算的运算顺序:先乘方,再乘除,后加减,有括号时先算括号里面的.
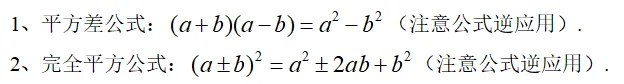
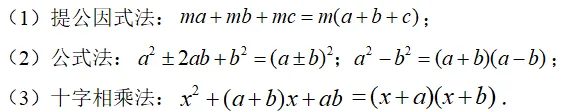
分解因式的基本步骤:
(1)先看各项有没有公因式,若有,则先提公因式;
(2)再看余下的式子能否用公式法继续分解,直至不能再分解为止.
简记为一“提”、二“套”、三“检查.







