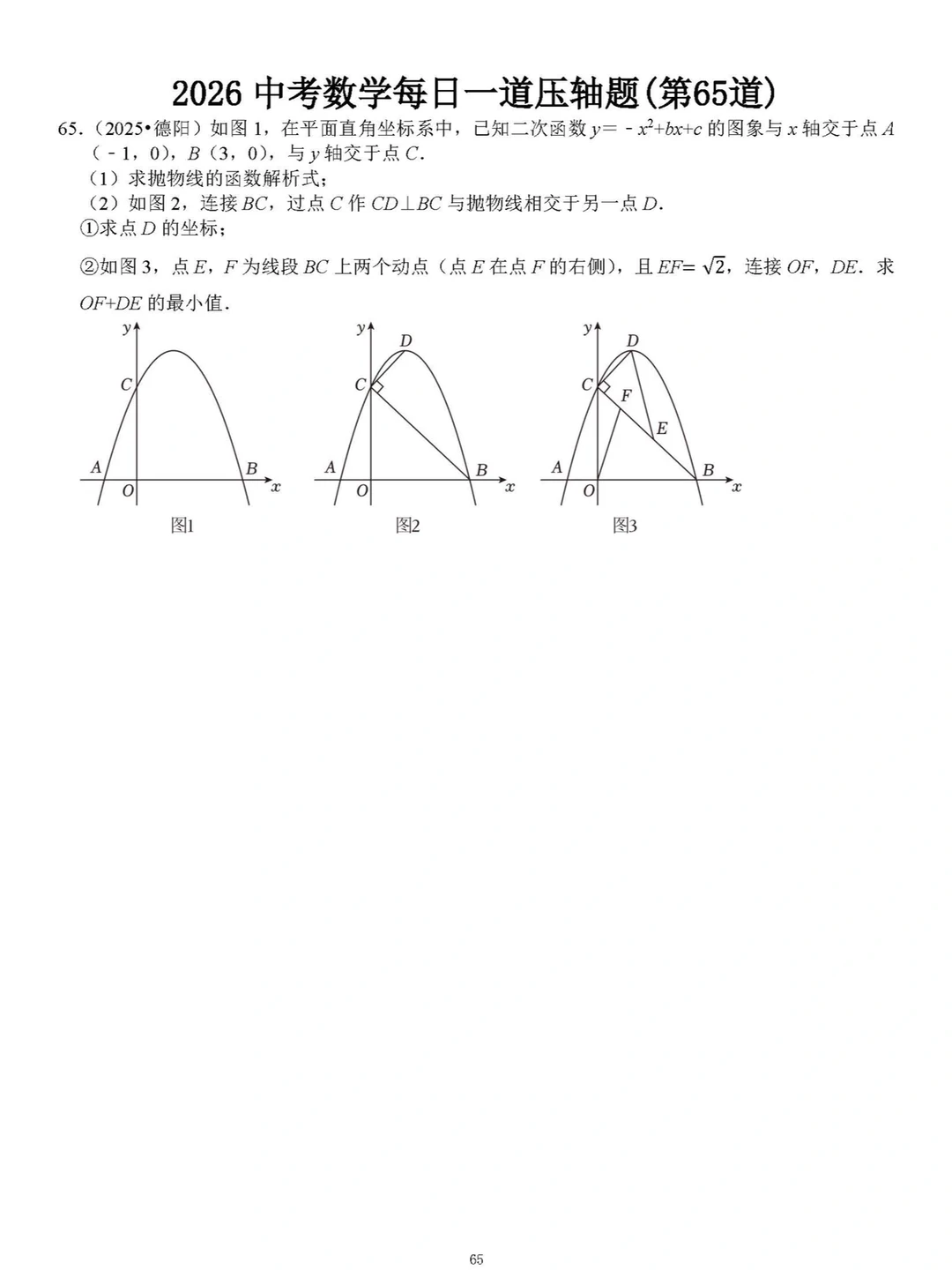

🌟 **中考数学压轴题精讲 | 二次函数+几何动点最值问题全解析!**
**🔍 这道德阳中考题太经典了!**
完美融合函数、几何与最值问题,一道题检验三大核心能力!
---
📚 **核心考点梳理:**
✅ **二次函数解析式求解**——已知交点用交点式秒解
✅ **函数与几何综合**——垂直条件转化为直线解析式求交点
✅ **动点最值问题**——通过平移构造平行四边形转化线段和
✅ **数形结合思想**——利用等腰直角三角形性质简化计算
---
💡 **解题精华解析:**
1️⃣ **第(1)问基础必拿分**
已知A(-1,0)、B(3,0) ⇒ 直接设交点式y=-(x+1)(x-3)
展开得y=-x²+2x+3
2️⃣ **第(2)①问几何转化**
CD⊥BC ⇒ 利用∠OBC=45°推导出∠CGB=45°
得G(-3,0) ⇒ 求直线CD解析式y=x+3
与抛物线联立解得D(1,4)
3️⃣ **第(2)②问最值技巧**
- 构造平行四边形OHEF,将OF转化为EH
- EF=√2 ⇒ 利用等腰Rt△得H(1,-1)
- DE+EH ≥ DH = 5(当D、E、H共线时取等号)
---
📌 **学习价值:**
▫️掌握“函数与几何综合题”的通用解题框架
▫️学会通过几何构造转化线段和的最值问题
▫️积累动点问题的处理经验
▫️培养数形结合的解题习惯
✨ **举一反三:**
这类“函数背景下的几何最值问题”是中考压轴题的标配,把这道题吃透,相当于掌握了这一类题的精髓!
---
#中考数学冲刺 #二次函数压轴题 #几何动点 #最值问题 #数形结合 #解题技巧 #初中数学 #数学思维 #学霸秘籍 #中考备考攻略
**🔍 这道德阳中考题太经典了!**
完美融合函数、几何与最值问题,一道题检验三大核心能力!
---
📚 **核心考点梳理:**
✅ **二次函数解析式求解**——已知交点用交点式秒解
✅ **函数与几何综合**——垂直条件转化为直线解析式求交点
✅ **动点最值问题**——通过平移构造平行四边形转化线段和
✅ **数形结合思想**——利用等腰直角三角形性质简化计算
---
💡 **解题精华解析:**
1️⃣ **第(1)问基础必拿分**
已知A(-1,0)、B(3,0) ⇒ 直接设交点式y=-(x+1)(x-3)
展开得y=-x²+2x+3
2️⃣ **第(2)①问几何转化**
CD⊥BC ⇒ 利用∠OBC=45°推导出∠CGB=45°
得G(-3,0) ⇒ 求直线CD解析式y=x+3
与抛物线联立解得D(1,4)
3️⃣ **第(2)②问最值技巧**
- 构造平行四边形OHEF,将OF转化为EH
- EF=√2 ⇒ 利用等腰Rt△得H(1,-1)
- DE+EH ≥ DH = 5(当D、E、H共线时取等号)
---
📌 **学习价值:**
▫️掌握“函数与几何综合题”的通用解题框架
▫️学会通过几何构造转化线段和的最值问题
▫️积累动点问题的处理经验
▫️培养数形结合的解题习惯
✨ **举一反三:**
这类“函数背景下的几何最值问题”是中考压轴题的标配,把这道题吃透,相当于掌握了这一类题的精髓!
---
#中考数学冲刺 #二次函数压轴题 #几何动点 #最值问题 #数形结合 #解题技巧 #初中数学 #数学思维 #学霸秘籍 #中考备考攻略
文章来源:
四季读书网
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!






