中考数学压轴题之二次函数相等角存在性问题

中考数学压轴题之二次函数相等角存在性问题

中考数学压轴题

二次函数

相等角存在性问题

【题型1】二次函数面积定值 相等角存在性问题

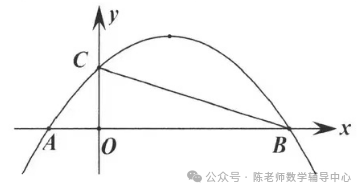
1.如图，已知点A(-1, 0),B(3, 0),C(0, 1)在抛物线y=ax²+bx+c上．

（1)求抛物线解析式；

（2)在直线BC上方的抛物线上求一点P,使ΔPBC面积为1;

（3)在x轴下方且在抛物线对称轴上，是否存在一点Q,使∠BQC=∠BAC?若存在，求出Q点坐标；若不存在，说明理由。

【题型2】二次函数内心在x轴上、相等角存在性问题

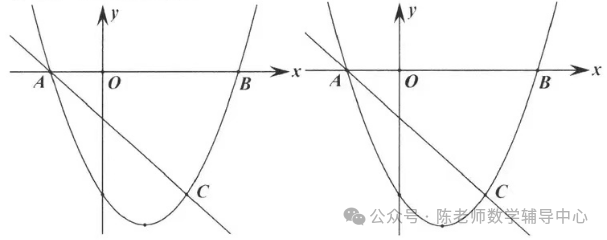
2.如图，已知：抛物线y=x²+bx+c与直线1交于点A(-1, 0),C(2,-3),与x轴另一交点为B.

（1)求抛物线的解析式；

（2)在抛物线上找一点P,使ΔACP的内心在x轴上，求点P的坐标；    

（3)M是抛物线上一动点，过点M作x轴的垂线，垂足为N,连接BM.在（2)的条件下，是否存在点M,使∠MBN=∠APC?若存在，请求出点M的坐标；若不存在，请说明理由。

数学陈老师:

【题型3】二次函数角度相等、四边形面积最大值

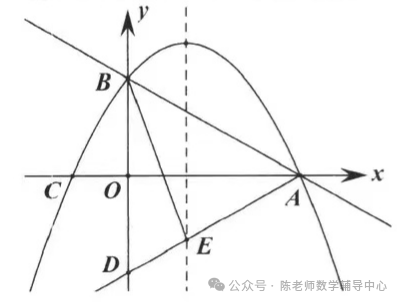
3.如图，在平面直角坐标系xOy中，一次函数y=-1/2x+3的图象与x轴交于点A,与y轴交于点B,点C的坐标为（－2, 0),抛物线经过A,B,C三点．

（1)求抛物线的解析式；

（2)直线AD与y轴负半轴交于点D,且∠BAO=∠DAO,求证：OB=0D;

（3)在（2)的条件下，若直线AD与抛物线的对称轴1交于点E,连接BE,在第一象限内的抛物线上是否存在一点P,使四边形BEAP的面积最大？若存在，请求出点P的坐标及四边形BEAP面积的最大值；若不存在，请说明理由。    

【题型4】二次函数面积定值、二倍角存在性问题

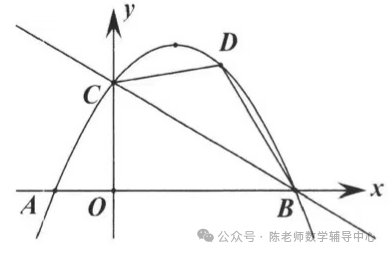
4.如图，抛物线y=ax²+bx+c经过A(-1, 0)、B(4, 0)、C(0, 2)三点，点D(x,y)为抛物线上第一象限内的一个动点。

（1)求抛物线所对应的函数表达式；

（2)当ΔBCD的面积为3时，求点D的坐标；

（3)过点D作DE⊥BC,垂足为点E,是否存在点D,使得ΔCDE中的某个角等于∠ABC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．

数学陈老师:

【题型5】二次函数相等角存在性问题讨论

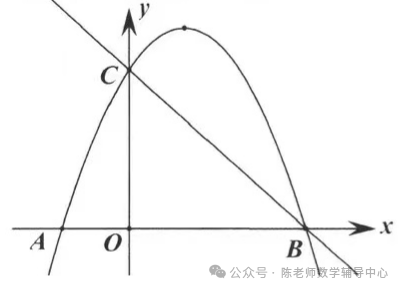
5.如图，已知二次函数y=-x²+bx+c的图象经过点A(-1, 0),B(3, 0),与y轴交于点C.

（1)求抛物线的解析式；

（2)抛物线上是否存在点P,使∠PAB=∠ABC,若存在请直接写出点P的坐标．若不存在，请说明理由。

【题型6】二次函数相等角存在性问题、线段比值的定值

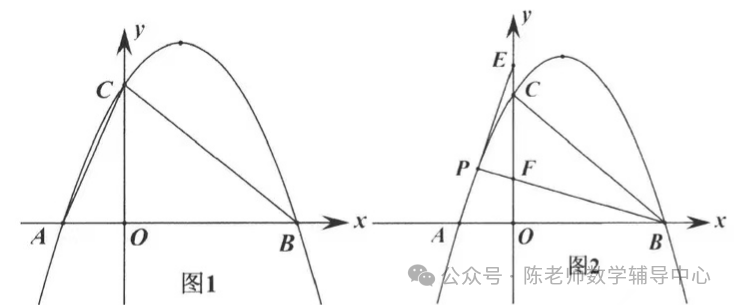
6.已知，抛物线y=ax²+bx+c经过A(-1, 0)、B(3, 0)、C(0, 3)三点，点P是抛物线上一点。

（1)求抛物线的解析式；

（2)当点P位于第四象限时，连接AC,BC,PC,若∠PCB=∠AC0,求直线PC的解析式；    

（3)如图2,当点P位于第二象限时，过P点作直线AP,BP分别交y轴于E,F

CE两点，请问CE/CF的值是否为定值？若是，请求出此定值；若不是，请说明理由。

数学陈老师:

【题型7】二次函数、铅垂定理面积最大值、相等角存在性问题

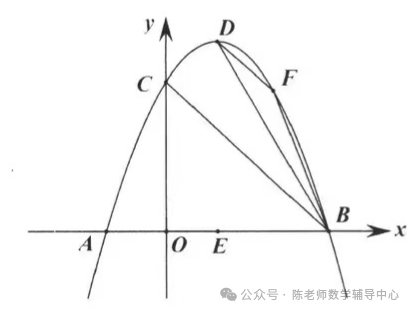
7.如图，已知抛物线y=ax²+bx+c与两坐标轴相交于点A(-1, 0)、B(3, 0)、C(0, 3),D是抛物线的顶点，E是线段AB的中点．

（1)求抛物线的解析式，并写出D点的坐标；

（2)F(x,y)是抛物线上的动点：

  ①当x＞1,y＞0时，求ΔBDF的面积的最大值；

  ②当∠AEF=∠DBE时，求点F的坐标。    

【题型8】二次函数将军饮马最小值、相等角存在性问题

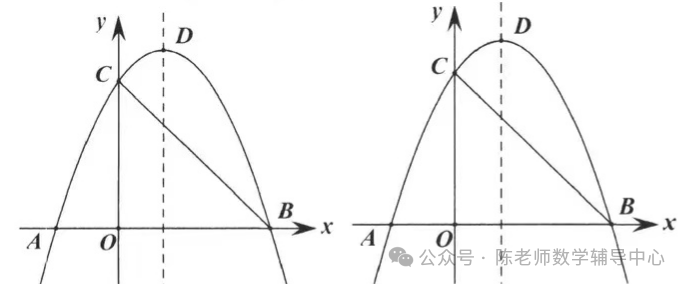
8.如图，直线y=-x+3与x轴、y轴分别交于B、C两点，抛物线y=-x²+bx+c经过点B、C,与x轴另一交点为A,顶点为D.

（1)求抛物线的解析式；

（2)在x轴上找一点E,使EC+ED的值最小，求EC+ED的最小值；

（3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在，求出P点坐标；若不存在，请说明理由。

数学陈老师:

【题型9】二次函数相等角存在性问题、动点翻折问题

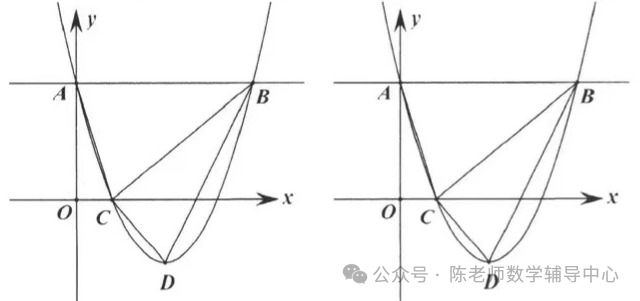
9.如图，二次函数y=x²+bx+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(1, 0),且顶点为D,连接AC、BC、BD、CD.

（1)填空：b=          ;

（2)点P是抛物线上一点，点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD=∠ACB,求点P的坐标；

（3)点E在直线AC上，点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG. 当点F在x轴上时，直接写出AG的长。

【题型10】二次函数铅垂定理面积最大值、相等角存在性问题

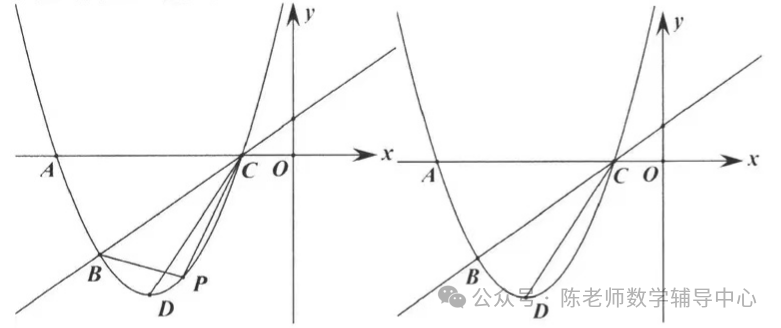
10.如图，已知抛物线y=ax²+bx+5经过A(-5, 0),B(-4,-3)两点，与x轴的另一个交点为C,顶点为D,连接CD.

（1)求该抛物线的表达式；    

（2)点P为该抛物线上一动点（与点B、C不重合），设点P的横坐标为t.

  ①当点P在直线BC的下方运动时，求ΔPBC的面积的最大值；

  ②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在，求出所有点P的坐标；若不存在，请说明理由。

点赞+关注

天天学习不迷路

赞赏后可获取电子版