2024年安徽省亳州市、芜湖市中考数学模拟试卷(5月份)
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.(4分)下列各数中是负数的是( )
A.|﹣3| B.﹣(﹣1) C.0 D.﹣2
【解答】解:A.|﹣3|=3>0,是正数,不符合题意.
B.﹣(﹣1)=1>0,是正数,不符合题意.
C.0既不是正数,也不是负数,不符合题意.
D.﹣2<0,是负数,符合题意.
故选:D.
2.(4分)计算(﹣a)6÷a的结果是( )
A.a6 B.﹣a6 C.a5 D.﹣a5
【解答】解:(﹣a)6÷a=a5.
故选:C.
3.(4分)2024年第一季度我省地区生产总值约为11300亿元,其中11300亿用科学记数法表示为( )
A.1.13×104 B.1.13×1012 C.1.13×1013 D.113×1010
【解答】解:11300亿即1130000000000大于1,用科学记数法表示为a×10n,其中a=1.13,n=12,
∴11300亿用科学记数法表示为1.13×1012,
故选:B.
4.(4分)某几何体的三视图如图所示,则该几何体是( )
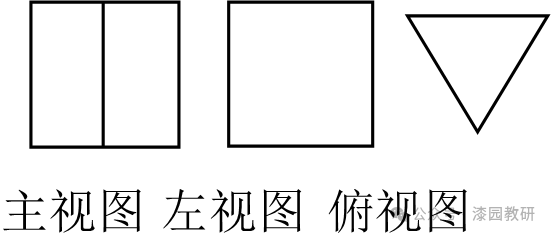
A.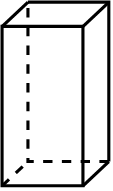 B.
B.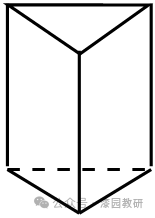 C.
C.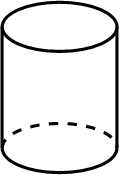 D.
D.
【解答】解:A的俯视图
C的俯视图

D的俯视图

都与题目给出的三视图矛盾.B的三视图为
,
故图中三视图对应的几何体不是选项A、C、D中图形,选项B的三视图与题目的三视图相一致.
故选:B.
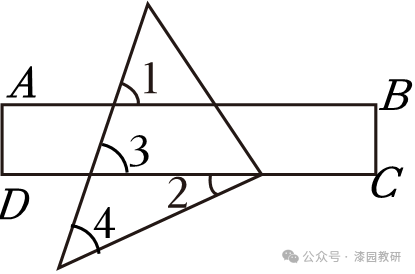
5.(4分)如图,一个45°角的三角板的直角顶点恰好在直尺的一边上,若∠1=70°,则∠2的度数为( )
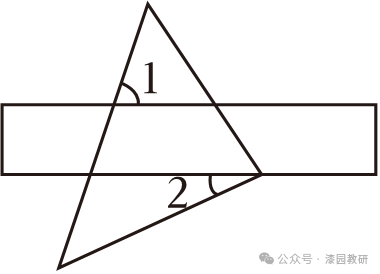
A.20° B.25° C.75° D.65°
【解答】解:∵AB∥CD,
∴∠3=∠1=70°,
∵∠4=45°,
∴∠2=∠3﹣∠4=25°.
故选:B.
6.(4分)一款纯电家用汽车电池容量为60Ah,电池的剩余电量y(Ah)与行驶路程x(km)之间满足一次函数关系.已知该汽车行驶100km时,电池的剩余电量为45Ah,行驶300km时,电池的剩余电量为15Ah.若该纯电家用汽车充满电,能行驶的最远路程为( )
A.350km B.400km C.450km D.500km
【解答】解:设电池的剩余电量y(Ah)与行驶路程x(km)之间的关系式为y=kx+b,
根据题意得,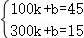
解得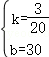
∴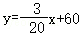
当y=0时,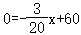
解得x=400,
∴该纯电家用汽车充满电,能行驶的最远路程为400km.
故选:B.
7.(4分)一个小组12名同学的出生月份(单位:月)如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
月份 | 3 | 6 | 8 | 6 | 11 | 5 | 7 | 8 | 8 | 7 | 8 | 7 |
则下列说法错误的是( )
A.这组数据的平均数是7
B.这组数据的众数是8
C.这组数据的中位数是6
D.这组数据的方差是3.5
【解答】解:A.平均数=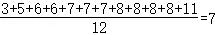 ,正确,该选项不符合题意;
,正确,该选项不符合题意;
B.8出现的次数最多,因此众数为8,正确,该选项不符合题意;
C.中位数: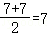 ,错误,该选项符合题意;
,错误,该选项符合题意;
D.数据的方差=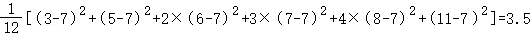 ,正确,该选项不符合题意.
,正确,该选项不符合题意.
故选:C.
8.(4分)如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,AD∥BC,则下列说法错误的是( )
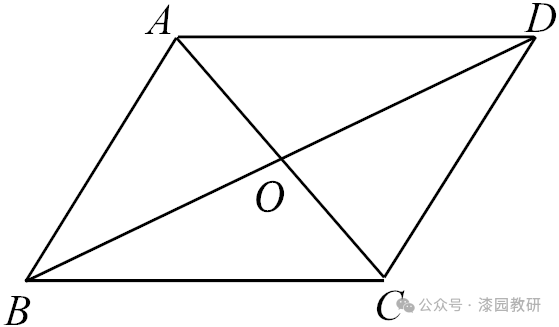
A.若AC=BD,则四边形ABCD是矩形
B.若BD平分∠ABC,则四边形ABCD是菱形
C.若AB⊥BC且AC⊥BD,则四边形ABCD是正方形
D.若AB=BC且AC⊥BD,则四边形ABCD是正方形
【解答】解:∵AD∥BC,
∴∠ADO=∠CBO,
∵OA=OC,∠AOD=∠BOC,
在△AOD和△COB中,
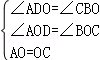
∴△AOD≌△COB(AAS),
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
若AC=BD,则四边形ABCD是矩形,故A选项不符合题意;
若BD平分∠ABC,
∴∠ABD=∠ADB,
∴AB=AD,
则四边形ABCD是菱形,故B选项不符合题意;
若AB⊥BC且AC⊥BD,则四边形ABCD是正方形,故C选项不符合题意;
若AB=BC且AC⊥BD,则四边形ABCD是菱形,故D选项符合题意;
故选:D.
9.(4分)二次函数y=ax2+2ax+b与一次函数y=ax+b(a,b是常数,且a≠0)在同一平面直角坐标系中的大致图象可能是( )
A.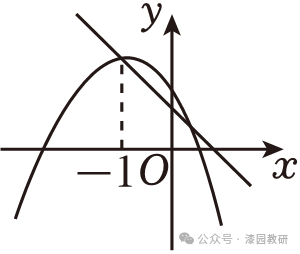 B.
B.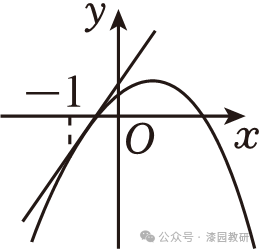
C.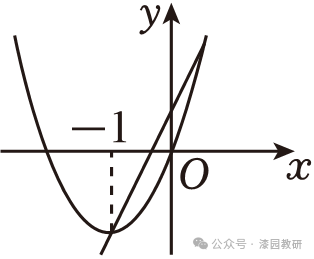 D.
D.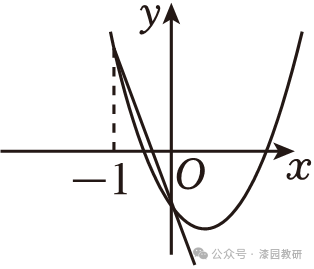
【解答】解:∵二次函数y=ax2+2ax+b,
∴对称轴为直线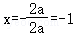 ,故B,D不符合题意;
,故B,D不符合题意;
∵当x=0时,y=ax2+2ax+b=b,y=ax+b=b,
∴二次函数与一次函数交于y轴上的点(0,b),故C不符合题意,A符合题意.
故选:A.
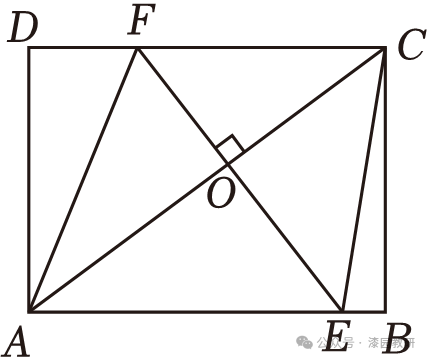
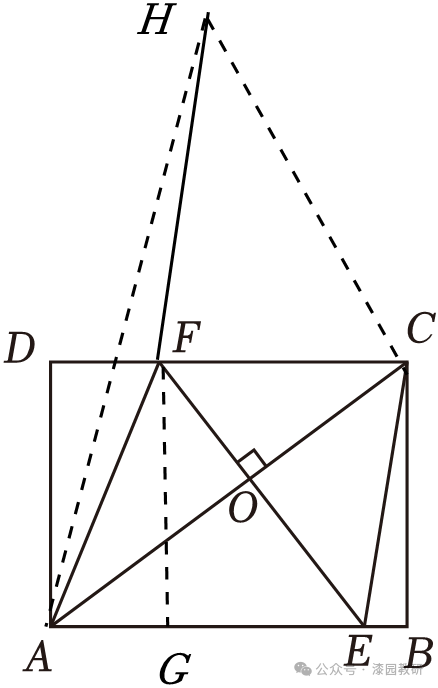
10.(4分)如图,在矩形ABCD中,AB=8,BC=6,E,F分别是边AB,CD上的点,EF⊥AC,垂足为点O,连接EC,AF,则EC+AF的最小值为( )
A.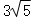 B.
B.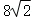 C.
C.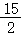 D.
D.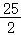
【解答】解:分别以EF、EC为边作平行四边形ECHF,连接AH,过点F作FG∥BC交AB于点G,则FG=BC=6,FH=EC,
∵AB=8,BC=6,
∴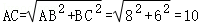
∵∠AOE=∠FGE=90°,∠BAC=90°﹣∠AEO=∠GFE,
∵∠ABC=∠FGE=90°,
∴△FGE∽△ABC,
∴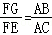
即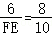
解得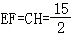
∵四边形ECHF是平行四边形,
∴EF∥CH,
∵AC⊥EF,
∴∠ACH=90°,
在Rt△ACH中,由勾股定理得:
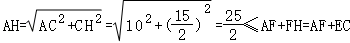
∴EC+FA的最小值为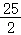
故选:D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.(5分)不等式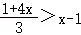 的解集是 x>﹣4 .
的解集是 x>﹣4 .
【解答】解: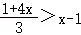
去分母得,1+4x>3(x﹣1),
去括号得,1+4x>3x﹣3,
移项,合并同类项得,x>﹣4.
故答案为:x>﹣4.
12.(5分)分解因式:x3﹣6x2+9x= x(x﹣3)2 .
【解答】解:x3﹣6x2+9x
=x(x2﹣6x+9)
=x(x﹣3)2,
故答案为:x(x﹣3)2.
13.(5分)如图,正方形OABC的边长为6,边OA,OC分别在x轴、y轴的正半轴上,顶点B在第一象限内,反比例函数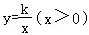 的图象与正方形OABC的两边AB,BC分别相交于点M,N.若△OMN的面积为10,则k的值为 24 .
的图象与正方形OABC的两边AB,BC分别相交于点M,N.若△OMN的面积为10,则k的值为 24 .
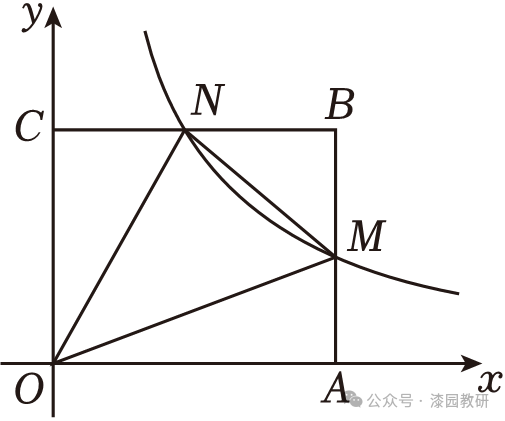
【解答】解:∵正方形OABC的边长为6,
∴OC=OA=AB=BC=6,
设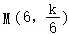
∴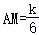
∵△OMN的面积为10,
∴S正方形OABC﹣S△OAM﹣S△OCN﹣S△BMN=10,
∴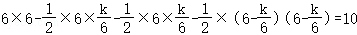
解得k=±24,
∵反比例函数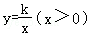 的图象在第一象限,
的图象在第一象限,
∴k=24.
故答案为:24.
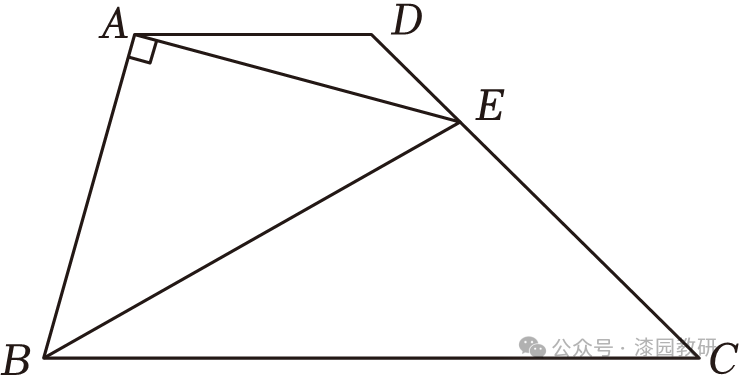
14.(5分)如图,在四边形ABCD中,AD∥BC,∠C=45°,以AB为腰作等腰直角三角形ABE,顶点E恰好落在CD边上.
(1)∠AED与∠EBC的大小关系是 相等 (填“相等”或“不相等”);
(2)若AD=2,则CE的长是 2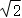 .
.
【解答】解:(1)∵等腰Rt△ABE,
∴∠BAE=90°,∠ABE=45°.
∵AD∥BC,
∴∠DAE+∠EBC=180°﹣90°﹣45°=45°,
∵∠C=45°,
∴∠D=180°﹣45°=135°,
∴∠D=180°﹣45°﹣135*,
∴∠AED=∠EBC;
故答案为:相等;
(2)如图.过点A作AF⊥BC于点F,过点E作GH⊥BC于点H,交AD的延长线于点G,
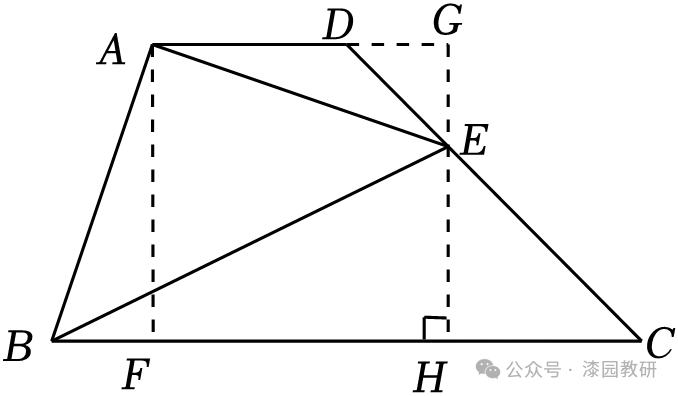
则∠AFB=∠CHE=90°,
∴AF∥GH,
∵AD∥BC,
∴AF=GH,∠AGE=90°,∠EDG=∠C=45°,
∵∠B A F+∠F A E=90°,∠E A G+∠F A E=90°,
∴∠BAF=∠EAG,
∵AB=AE,∠AFB=∠AGE=90°,
∴△AFB≌△AGE(AAS),
∴AF=AG,
∴AG=GH,
∵∠EDG=∠C=45°,
∴△CHE和△DGE是等腰直角三角形,
∴DG=EG,CH=EH,
∴AD=EH=CH=2,
由勾股定理得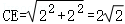 .
.
故答案为: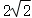 .
.
三、(本大题共2小题.每小题8分,满分16分)
15.(8分)计算: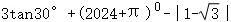 .
.
【解答】解:原式=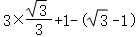
=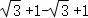
=2.
16.(8分)如图,在边长为1个单位长度的小正方形组成的网格中,△ABC是格点三角形,点D,E均为格点(网格线的交点).
(1)画出△ABC关于直线DE对称的△A1B1C1;
(2)将(1)中的△A1B1C1绕点C1逆时针旋转90°得到△A2B2C1,画出△A2B2C1.
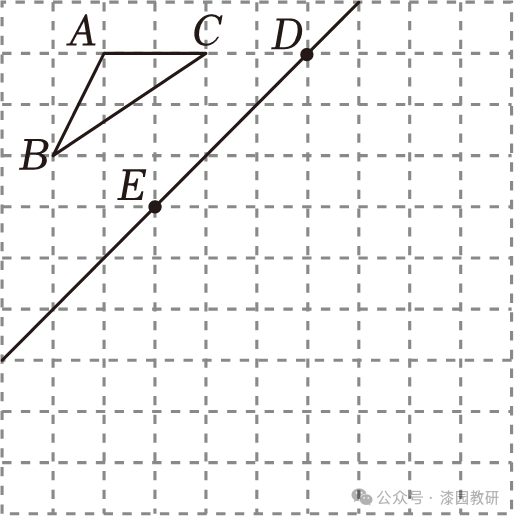
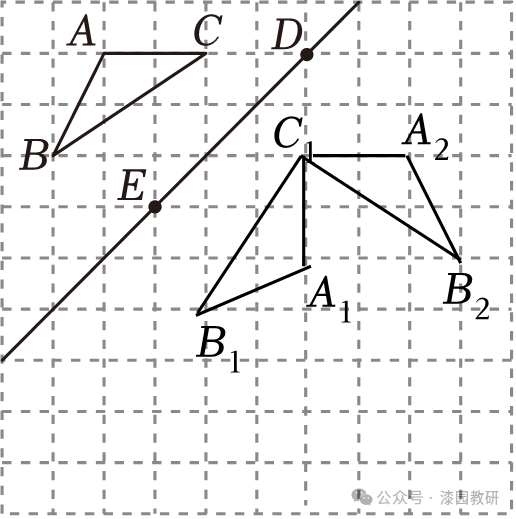
【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C1即为所求;
四、(本大题共2小题,每小题8分,满分16分)
17.(8分)《孙子算经》中有这样一道问题:今有百鹿入城,家取一鹿,不尽,又三家共一鹿,始尽.问城中家几何?大意是:今有100头鹿进城,每户分一头鹿后,没有分完,将剩下的鹿按每3户共分一头,恰好分完,问:城中有多少户人家?请解答上述问题.
【解答】解:设城中有x户人家,
根据题意得:x+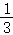 x=100,
x=100,
∴ x=100,
x=100,
解得:x=75.
答:城中有75户人家.
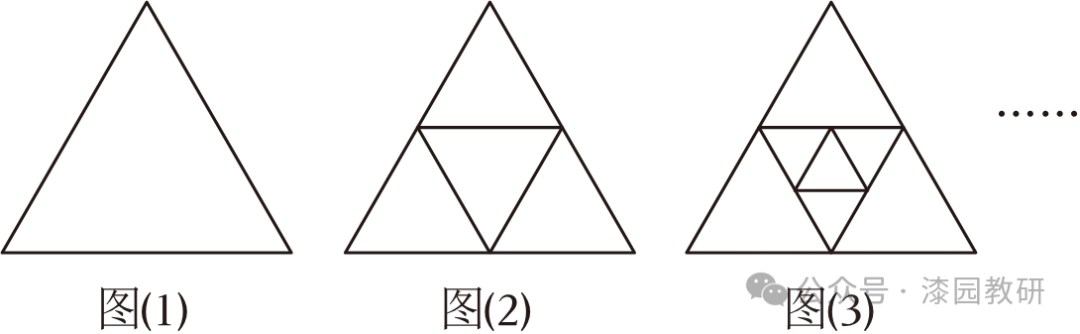
18.(8分)图1有1个三角形,记作a1=1;分别连接这个三角形三边中点得到图2,有1+4×1=5个三角形,记作a2=5;再分别连接图2中间的小三角形三边中点得到图3,有1+4×2=9个三角形,记作a3=9;…….根据上述规律,解答下面的问题:
(1)图4中有 13 个三角形,记作a4= 13 .
(2)猜想图n中有 (4n﹣3) 个三角形,记作an= 4n﹣3 ;(用含n的代数式表示)
(3)求a1+a2+a3+⋯+an的值.(结果用含n的代数式表示)
【解答】解:(1)∵第一个图中1个三角形,
第二个图中5个三角形,
第三个图中9个三角形,
∴图4中有13个三角形,记作a4=13
(2)由(1)可得,
图n中有(4n﹣3)个三角形,记作an=4n﹣3;
(3)a1+a2+a3+⋯+an
=4×1﹣3+4×2﹣3+4×3﹣3+•••+4n﹣3
=4×(1+2+3+•••+n)﹣3n
=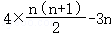
=2n(n+1)﹣3n
=2n2﹣n.
五、(本大题共2小题,每小题10分,满分20分)
19.(10分)如图,四边形ABCD是一个零部件的截面示意图,由相邻两个直角三角形组合而成,作菱形AEFG,使点E,G分别在边AB,AD上,点F在对角线BD上,已知AD=CD,,若菱形AEFG的边长为3dm,求该零部件截面ABCD的面积.(结果保留根号)
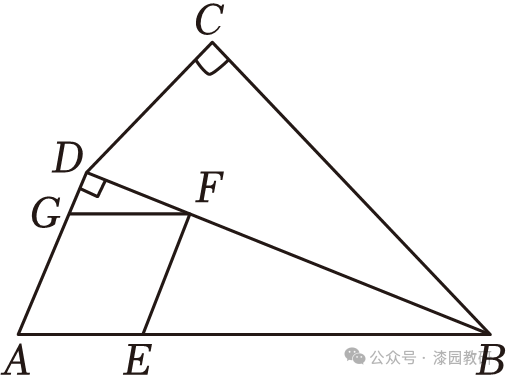
【解答】解:∵四边形AEFG是菱形,
∴A E=E F=F G=A G=3,EF∥AD,
∴∠BFE=90°,
在Rt△BEF中,
∵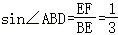
∴B E=3 E F=9,
∴A B=A E+B E=3+9=12(dm),
在Rt△ABD中,
∵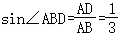
∴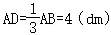
∴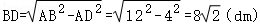 D=A D=4(dm),
D=A D=4(dm),
在Rt△BCD中,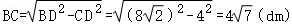
∴四边形ABCD的面积为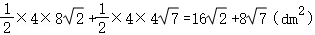
即该零部件截面ABCD的面积为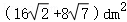 .
.
20.(10分)如图,AB是⊙O的直径,C,D是⊙O上的两点,且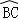 =
=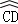 交AC于点E,点F在AC的延长线上,BE=BF.
交AC于点E,点F在AC的延长线上,BE=BF.
(1)求证:BF是⊙O的切线;
(2)若EF=18, .求⊙O的半径.
.求⊙O的半径.
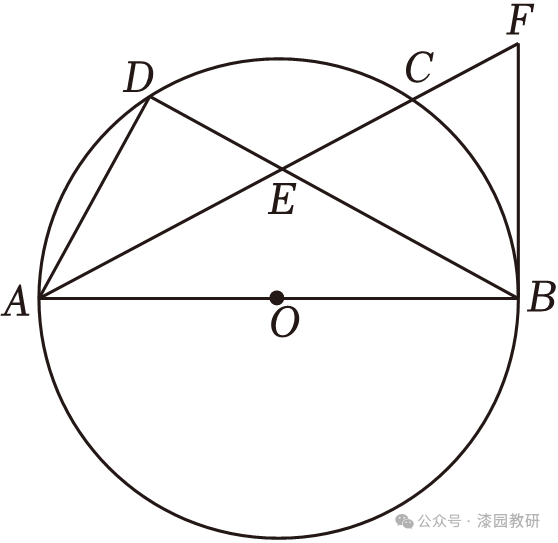
【解答】(1)证明:如图所示,连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CEB+∠CBE=90°,
∵BE=BF,
∴∠CEB=∠F,
∵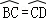
∴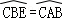
∴∠F+∠C A B=90°,
∴∠ABF=180°﹣90°=90°,
∴AB⊥BF,
∴BF是⊙O的切线;
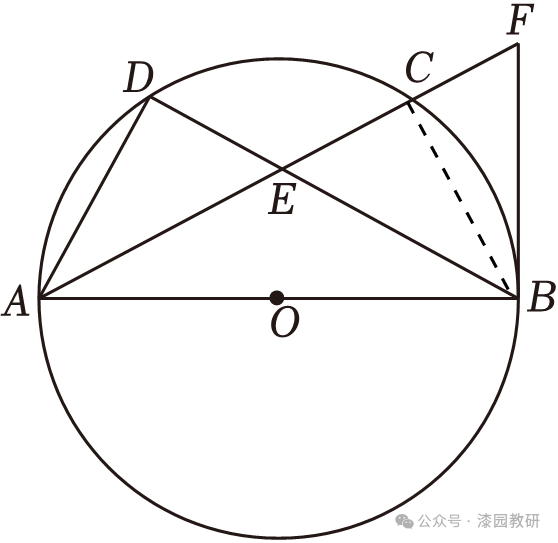
(2)解:∵BE=BF,∠ACB=90°,
∴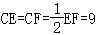
在Rt△BCF中,
∵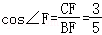
∴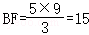 ;
;
在Rt△ABF中,
∵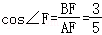
∴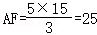
∴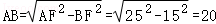
∴⊙O的半径为10.
六、(本题满分12分)
21.(12分)“吃粽子,赛龙舟”是端午节的习俗,一直保留至今,某校为了解学生对端午节习俗的喜爱程度,随机抽取了部分学生进行调查,通过调查统计,将该校学生对端午节习俗的喜爱程度分为四个等级:A.非常喜爱,B.比较喜爱,C.一般喜爱,D.不喜爱.并绘制了条形统计图和扇形统计图,部分信息如下:
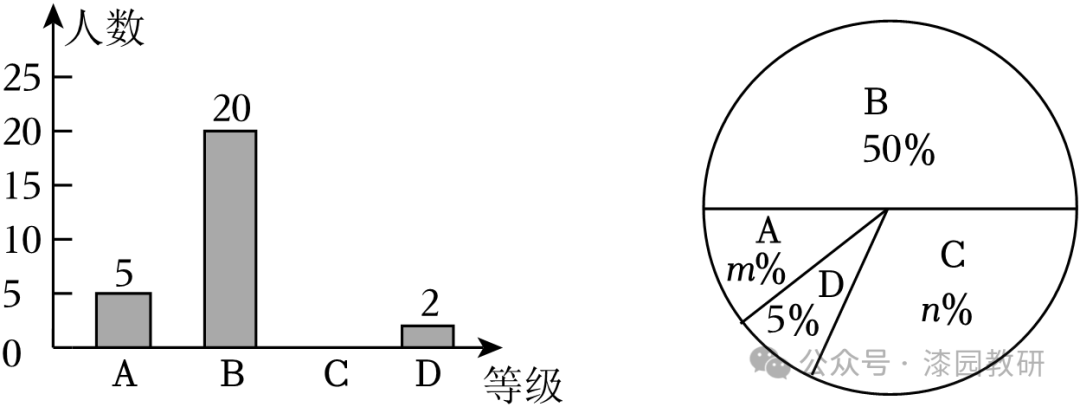
(1)这次抽查的学生人数是 40 人,图中m= 12.5 ,n= 32.5 ,补全条形统计图;
(2)已知该校在校学生人数为2800人,请估计该校对端午节习俗“一般喜爱”的人数;
(3)老师计划从对端午节习俗非常喜爱的甲、乙、丙、丁、戊五名学生中选取两人参加学校组织的端午节习俗宣讲活动,请用“列表法”或“画树状图法”,求出甲、乙至少有一人参加了端午节习俗宣讲活动的概率.
【解答】解:(1)这次抽查的学生人数为:2÷5%=40(人),
则C的人数为:40﹣5﹣20﹣2=13(人),
∵m%=5÷40×100%=12.5%,n%=13÷40×100%=32.5%,
∴m=12.5,n=32.5,
条形统计图补充完整如下:
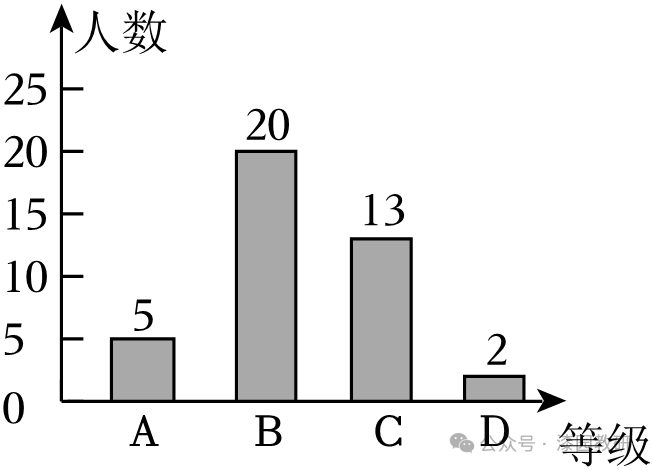
故答案为:40,12.5,32.5;
(2)估计该校对端午节习俗“一般喜爱”的人数为2800×32.5%=910(人);
(3)画树状图如下:
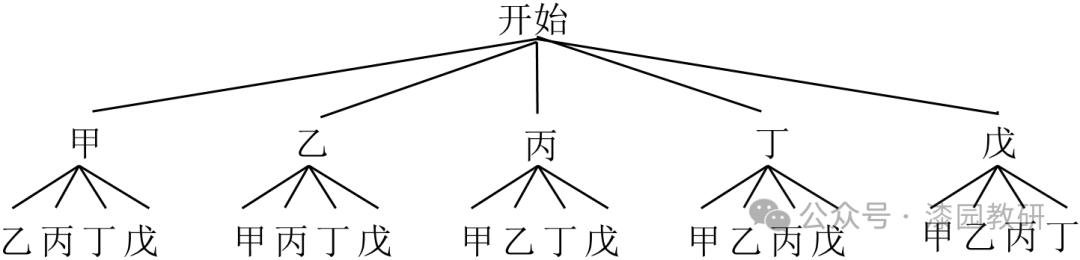
共有20种等可能的结果,其中甲、乙至少有一人参加了端午节习俗宣讲活动的结果有14种,
∴甲、乙至少有一人参加了端午节习俗宣讲活动的概率为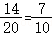 .
.
七、(本题满分12分)
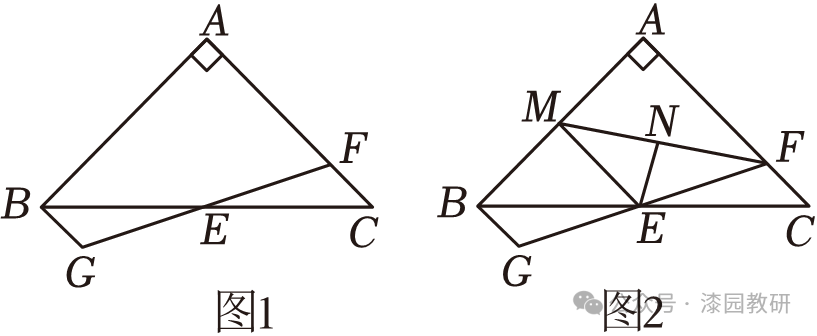
22.(12分)如图1,在△ABC中,AB=AC,∠A=90°,点E是边BC的中点,点F在边AC上,连接FE并延长到点G,使EG=EF.(1)求证:BG⊥AB;
(2)如图2,点M是边AB的中点,连接EM,FM,EN平分∠MEC交FM于点N,若BE=BM+BG,求证:MN=FN.
【解答】证明:(1)∵AB=AC,∠A=90°,
∴∠ABC=∠ACB=45°,
∵点E是边BC的中点,
∴BE=CE,
又∵∠BEG=∠CEF,EG=EF,
∴△BEG≌△CEF(SAS),
∴∠EBG=∠ECF=45°,
∴∠ABG=∠ABC+∠EBG=90°,即BG⊥AB;
(2)如图,延长EN交AC于点H,
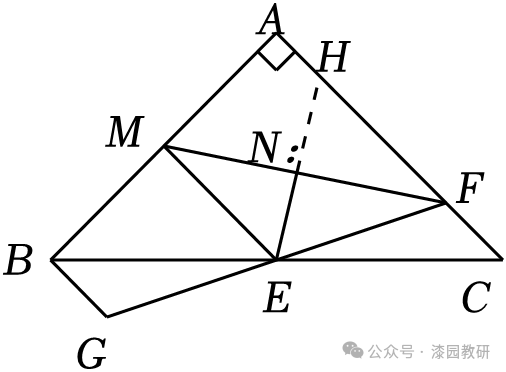
∵点M是AB的中点,点E是BC的中点,
∴EM∥AC,
∴∠MEN=∠CHE,
∵EN平分∠MEC,
∴∠MEN=∠CEH,
∴∠CHE=∠CEH,
∴CE=CH,
由(1)知△BEG≌△CEF,
∴BG=CF,
∵BE=BM+BG,CH=FH+CF,BE=CE,
∴BE=CE=CH,即BM+BG=FH+CF,
∴BM=FH,
∵AB=AC,EM∥AC,
∴∠MBC=∠C=∠MEB,
∴BM=EM,
∴FH=EM,
又∵∠MEN=∠FHE,∠MNE=∠FNH,
∴△MNE≌△FNH(AAS),
∴MN=FN.
八、(本题满分14分)
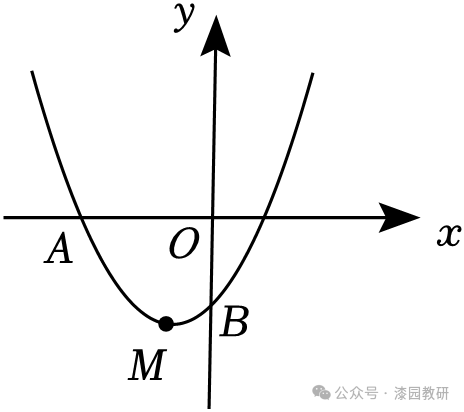
23.(14分)已知,抛物线y=ax2+2ax+c经过点A(﹣3,0),其顶点为M.
(1)求点M的坐标(用a表示);
(2)若该抛物线与y轴的交点为B,如图.
①当△ABM的面积为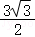 时,求a的值;
时,求a的值;
②当△ABM为直角三角形时,求点B的坐标.
【解答】解:(1)∵抛物线y=ax2+2ax+c经过点A(﹣3,0),
∴0=9 a﹣6 a+c,
∴c=﹣3a,
∵y=ax2+2ax+c=ax2+2ax﹣3a=a(x2+2x)﹣3a=a(x+1)2﹣4a,
∴顶点M的坐标为(﹣1,﹣4a).
(2)①当x=0时,y=c=﹣3 a,
∴抛物线与y轴的交点B的坐标为(0,﹣3a).
如图所示,过点M作平行于y轴的直线l交x轴于点E,交AB于点F,过点B作BN⊥l于点N,
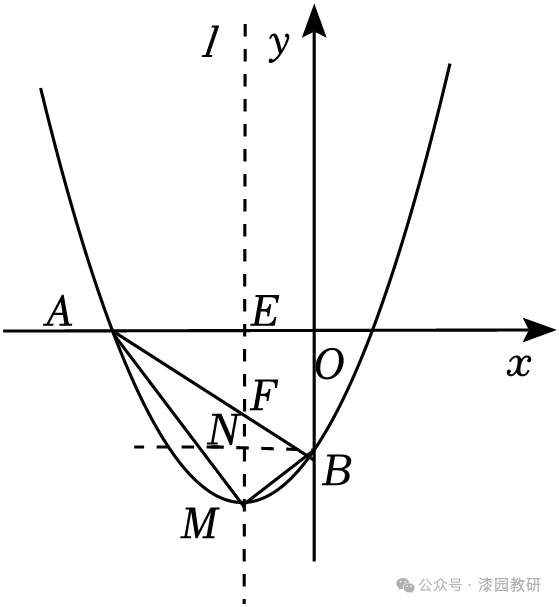
∴S△ABM=S△AMF+S△BMG
=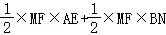
=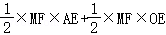
=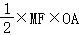
设直线AB的表达式为y=kx+b,
把B(0,﹣3a),A(﹣3,0)代入
得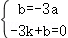
解得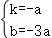
∴直线AB的表达式为y=﹣ax﹣3a,
当x=﹣1时,y=﹣2a,
∴点F的坐标为(﹣1,﹣2a),
∴M F=2 a,
∴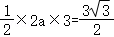
解得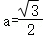 ;
;
②由①得点M的坐标为(﹣1,﹣4a),点B的坐标为(0,﹣3a).
∴AM2=22+(﹣4a)2=4+16a2,
BM2=(﹣1)2+(﹣a)2=1+a2,AB2=(﹣3)2+(3a)2=9+9a2,
∵△ABM为直角三角形,
∴分以下几种情况:
当∠AMB=90°时,AM2+BM2=AB2,
∴4+16 a2+1+a2=9+9a2,
整理得8a2=4,
解得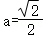 或
或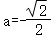 (舍去),
(舍去),
∴点B的坐标为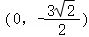 ;
;
当∠ABM=90°时,AB2+BM2=AM2,
∴9+9a2+1+a2=4+16a2,
整理得6a2=6,
解得a=1或a=﹣1(舍去),
∴点B的坐标为(0,﹣3);
当∠MAB=90°时,AB2+AM2=BM2,
∴9+9a2+4+16a2=1+a2,
整理得24a2=﹣12,此方程无实数解;
综上,点B的坐标为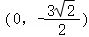 或(0,﹣3).
或(0,﹣3).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2024/6/5 20:18:02;用户:安徽蒙城双涧中学;邮箱:mcsjzx@xyh.com;学号:24963525






