中考数学压轴题之新函数图像探究题类型五函数图象平移

中考数学压轴题之新函数图像探究题类型五函数图象平移

中考数学压轴题

新函数图像探究题

类型五、函数图象平移

  新函数图像探究题是近些年中考数学的一种新题型，在各地的中考数学试卷中已有出现，在近年越来越频繁地出现在全国各省市的中考数学试卷中。

  新函数图像探究题是建立在学生已经学习的正比例函数、一次函数、反比例函数和二次函数基础之上，将基本函数进行组合、变形、平移等形成新的函数，是对函数图像与性质的综合运用。

  在初中阶段的函数学习中，我们经历了“确定函数的表达式－－利用函数图象研究其性质－－运用函数解决问题”的学习过程。新函数图像的探究题的学习也是同样的过程，作出函数图像是解题的关键，在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象。

  画函数图像一般需要经历分析解析式、列表、描点、连线过程得到函数图象，一般情况下是草图，但需要抓住几个关键点和基本走势，然后通过通过观察、对比、分析探究函数图像的性质，解决问题。

  函数图像探究题作为近些年中考的新题型，注重对学生观察、分析、解决问题的能力及知识迁移和运用能力的考查，具有一定的综合性和跳跃性，在学习中需要不断去总结和思考，掌握常见类型的题目的解题思路和方法。

  函数图象性质的探究题常见问题：

  ①求自变量的取值范围：根据解析式中分式、二次根式等有意义的条件，列出不等式（组）进行求解；    

  ②描点、连线画函数图象：用平滑的曲线依次连接各点即可；

  ③写函数的相关性质：根据函数图象，从最值、增减性、对称性、最值点、特殊点等方面入手即可；

  ④函数与方程或不等式综合考查，观察函数图像求值或取值范围，理解函数图像的交点的坐标与方程的解的关系，掌握在同一坐标系中不同函数的值的大小与函数图像的位置关系是解题的关键。

  综合全国各省市往年的中考真题及模考题，整理出了新函数图像探究题一般常见的六种类型：

五、函数图象平移

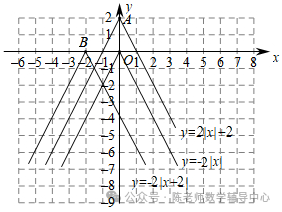
1、函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索．画函数y=-2|x|的图象，经历分析解析式、列表、描点、连线过程得到函数图象如图所示；经历同样的过程画函数y=－2|x|+2和y=-2|x+2|的图象如图所示：

（1)观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解析式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化。写出点A,B的坐标和函数y=－2|x+2|的对称轴；

（2)探索思考：平移函数y=-2|x|的图象可以得到函数y=-2| x|+2和y=-2|x+2|的图象，分别写出平移的方向和距离；    

（3)拓展应用：在所给的平面直角坐标系内画出函数y=-2|x-3|+1的图象．若点（x₁ ,y₁)和（x₂ ,y₂)在该函数图象上，且x₂＞x₁＞₃ ,比较y₁,y₂的大小．

数学陈老师:

2、模具厂计划生产面积为4,周长为m的矩形模具．对于m的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：

（1)建立函数模型

设矩形相邻两边的长分别为x,y.由矩形的面积为4,得xy=4,即y=4/x;由周长为m,得2(x+y)=m,即y=-x+m/2满足要求的（x,y)应是两个函数图象在第      象限内交点的坐标；

（2)画出函数图象

函数y=4/x(x＞0)的图象如图所示，而函数y=-x+m/2的图象可由直线y=-x平移得到。请在同一直角坐标系中直接画出直线y=-x;    

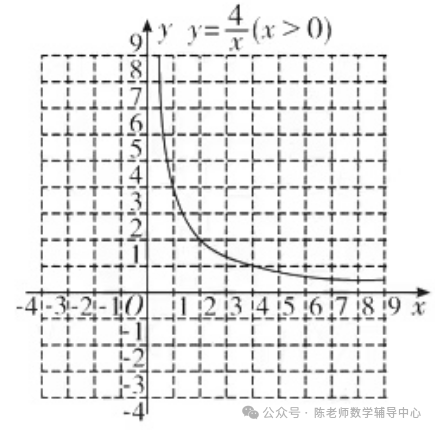
（3)平移直线y=-x,观察函数图象

  ①当直线平移到与函数y=4/x(x＞0)的图象有唯一交点（2, 2)时，周长m的值为          ;

  ②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长m的取值范围；

（4)得出结论

若能生产出面积为4的矩形模具，则周长m的取值范围为           .

数学陈老师:

3、小明根据学习函数的经验，对函数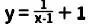的图象与性质进行了探究，下面是小明的探究过程，请补充完整：    

（1)函数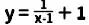的自变量x的取值范围是           ;

（2)下表列出了y与x的几组对应值，请写出m,n的值：m=      ；n=     ;

（3)在如图所示的平面直角坐标系中，描全上表中以各对对应值为坐标的点，并画出该函数的图象；

（4)结合函数的图象，解决问题：

  ①写出该函数的一条性质           ;

  ②当函数值 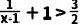 时，x的取值范围是          ;

  ③方程 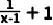 =x 的解为              .    

数学陈老师:

4、某班“数学兴趣小组”对函数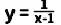的图象和性质进行了探究探究过程如下，请补充完成：

（1)函数 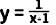的自变量x的取值范围是          ；

（2)下表是y与x的几组对应值．请直接写出m,n的值：m=     ;n=      ;

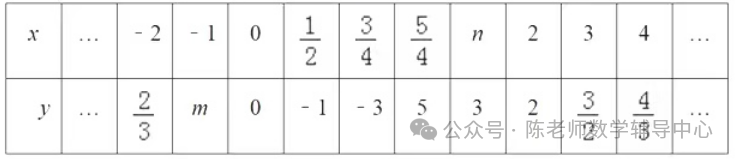
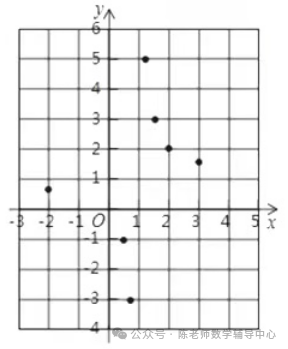
（3)如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

（4)通过观察函数的图象，小明发现该函数图象与反比例函数y=k/x（k＞0)的图象形状相同，是中心对称图形，且点（－1,m)和（3,3/2）是一组对称点，则其对称中心的坐标为          ;

（5)当2≤x≤4时，关于x的方程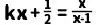有实数解，求k的取值范围。    

数学陈老师:

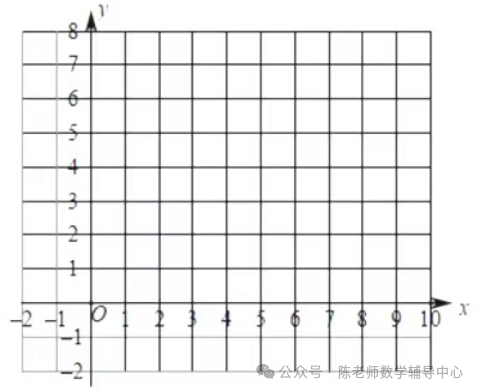
5、在平面直角坐标系xOy中，直线x=5与直线y=3,x轴分别交于点A,B,直线y=kx+b(k≠0)经过点A且与x轴交于点C(9, 0).

（1)求直线y=kx+b的表达式；

（2)横、纵坐标都是整数的点叫做整点．记线段AB,BC,CA围成的区域（不含边界）为W.

  ①结合函数图象，直接写出区域W内的整点个数；

  ②将直线y=kx+b向下平移n个单位，当平移后的直线与区域W没有公共点时，请结合图象直接写出n的取值范围。    

数学陈老师:

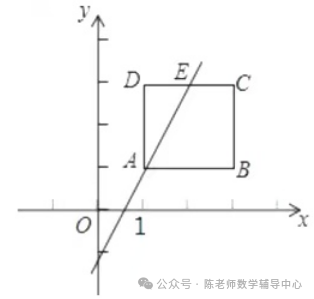
6、如图，在正方形ABCD中，A(1, 1)、B(3, 1),点E是DC的中点．

（1)求直线AE的解析式；

（2)设直线l与y轴交点的坐标为（0,b),当直线l//AE且与边AB、CD同时有交点时，直接写出b的取值范围。    

点赞+关注

学习更优秀

赞赏可得电子版