中考数学: 二次函数与几何的综合专题突破

学而时习之，不亦说乎！

点击关注我们共同进步！

1、二次函数与特殊四变形的综合

2、二次函数与最值的综合

3、二次函数与相似的综合

4、二次函数与新定义的综合

有需要电子版的朋友们请至文末获取哦！

题型一：二次函数与特殊四边形的综合

【中考真题练】

1．（2023•扬州）在平面直角坐标系xOy中，已知点A在y轴正半轴上．

（1）如果四个点（0，0）、（0，2）、（1，1）、（﹣1，1）中恰有三个点在二次函数y＝ax²（a为常数，且a≠0）的图象上．

①a＝   ；

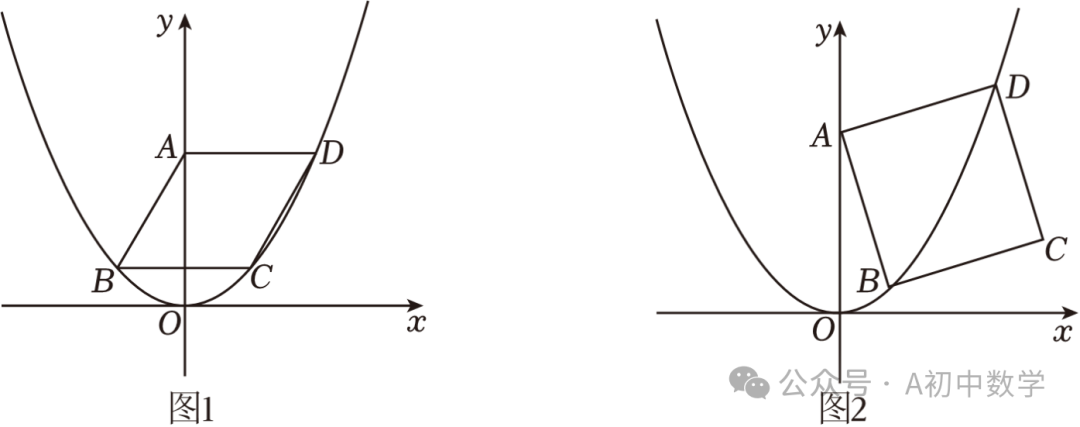
②如图1，已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；

③如图2，已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n，试探究n﹣m是否为定值．如果是，求出这个值；如果不是，请说明理由．

（2）已知正方形ABCD的顶点B、D在二次函数y＝ax²（a为常数，且a＞0）的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n，直接写出m、n满足的等量关系式．

2．（2023•枣庄）如图，抛物线y＝﹣x²+bx+c经过A（﹣1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于点D．

（1）求该抛物线的表达式；

（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；

（3）若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．

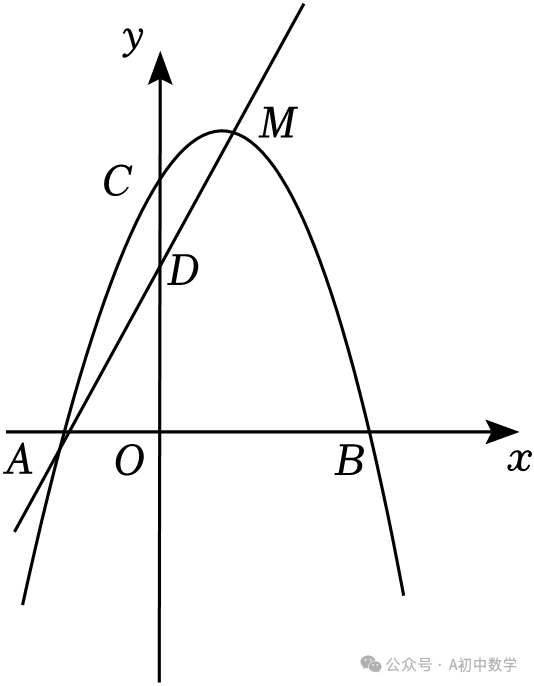
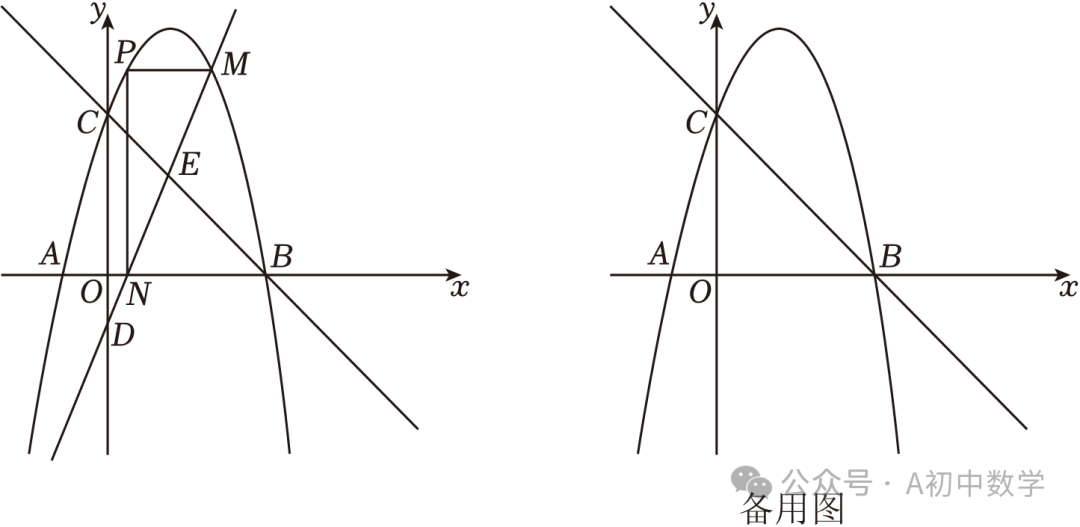
3．（2023•济宁）如图，直线y＝﹣x+4交x轴于点B，交y轴于点C，对称轴为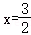的抛物线经过B，C两点，交x轴负半轴于点A，P为抛物线上一动点，点P的横坐标为m，过点P作x轴的平行线交抛物线于另一点M，作x轴的垂线PN，垂足为N，直线MN交y轴于点D．

（1）求抛物线的解析式；

（2）若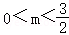，当m为何值时，四边形CDNP是平行四边形？

（3）若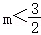，设直线MN交直线BC于点E，是否存在这样的m值，使MN＝2ME？若存在，求出此时m的值；若不存在，请说明理由．

【中考模拟练】

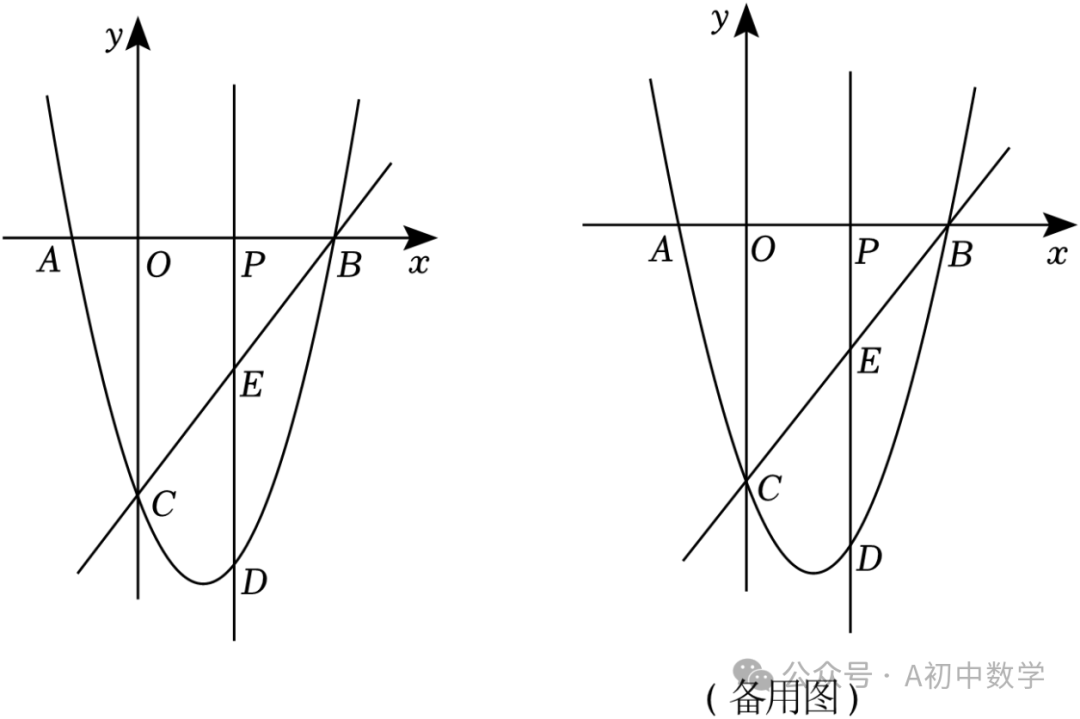
1．（2024•新沂市模拟）如图，在平面直角坐标系中，二次函数y＝ax²+bx﹣3的图象交x轴于A（﹣1，0）、B（3，0）两点，交y轴于点C，点P在线段OB上，过点P作PD⊥x轴，交抛物线于点D，交直线BC于点E．

（1）a＝   ，b＝    ；

（2）在点P运动过程中，若△CDE是直角三角形，求点P的坐标；

（3）在y轴上是否存在点F，使得以点C、D、E、F为顶点的四边形为菱形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

题型二：二次函数与最值的综合

【中考真题练】

1．（2023•荆州）已知：y关于x的函数y＝（a﹣2）x²+（a+1）x+b．

（1）若函数的图象与坐标轴有两个公共点，且a＝4b，则a的值是             ；

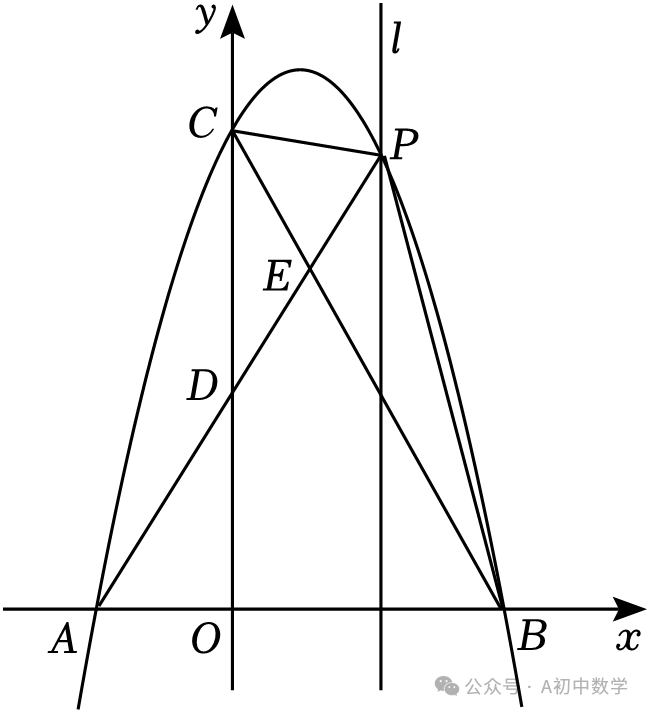
（2）如图，若函数的图象为抛物线，与x轴有两个公共点A（﹣2，0），B（4，0），并与动直线l：x＝m（0＜m＜4）交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为S₁，△CDE的面积为S₂．

①当点P为抛物线顶点时，求△PBC的面积；

②探究直线l在运动过程中，S₁﹣S₂是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．

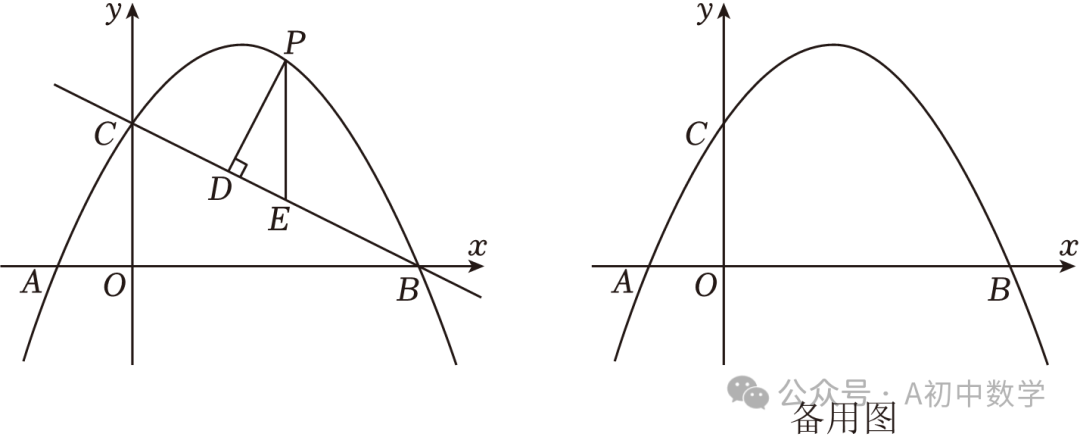
2．（2023•重庆）如图，在平面直角坐标系中，抛物线y＝ax²+bx+2过点（1，3），且交x轴于点A（﹣1，0），B两点，交y轴于点C．

（1）求抛物线的表达式；

（2）点P是直线BC上方抛物线上的一动点，过点P作PD⊥BC于点D，过点P作y轴的平行线交直线BC于点E，求△PDE周长的最大值及此时点P的坐标；

（3）在（2）中△PDE周长取得最大值的条件下，将该抛物线沿射线CB方向平移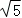个单位长度，点M为平移后的抛物线的对称轴上一点．在平面内确定一点N，使得以点A，P，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．

【中考模拟练】

1．（2024•东平县一模）如图，在平面直角坐标系中，点A、B在x轴上，点C、D在y轴上，且OB＝OC＝3，OA＝OD＝1，抛物线y＝ax²+bx+c（a≠0）经过A、B、C三点，直线AD与抛物线交于另一点M．

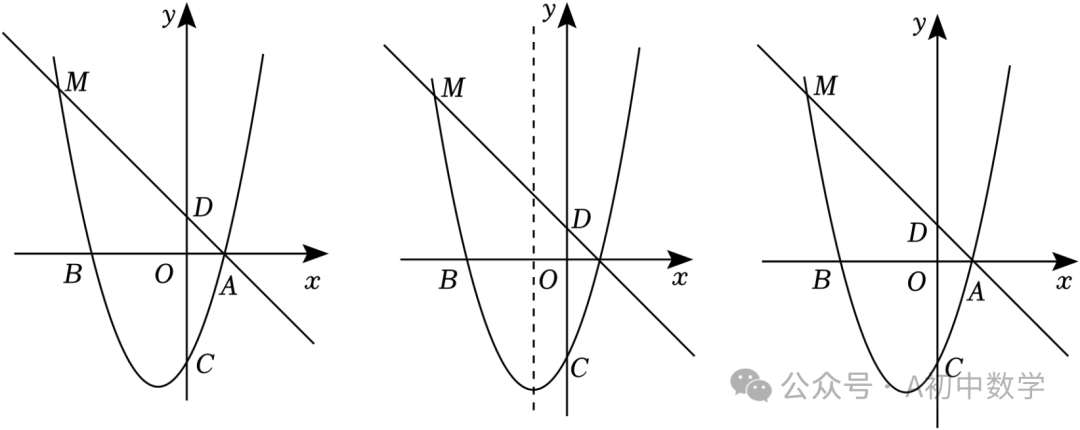
（1）求这条抛物线的解析式；

（2）在抛物线对称轴上是否存在一点N，使得△ANC的周长最小，若存在，请求出点N的坐标，若不存在，请说明理由；

（3）点E是直线AM上一动点，点P为抛物线上直线AM下方一动点，EP∥y轴，当线段PE的长度最大时，请求出点E的坐标和△AMP面积的最大值．

题型三：二次函数与相似的综合

【中考真题练】

1．（2023•乐至县）如图，直线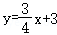与x轴、y轴分别交于A、B两点，抛物线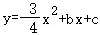经过A、B两点．

（1）求抛物线的表达式；

（2）点D是抛物线在第二象限内的点，过点D作x轴的平行线与直线AB交于点C，求DC的长的最大值；

（3）点Q是线段AO上的动点，点P是抛物线在第一象限内的动点，连结PQ交y轴于点N．是否存在点P，使△ABQ与△BQN相似，若存在，求出点P的坐标；若不存在，说明理由．

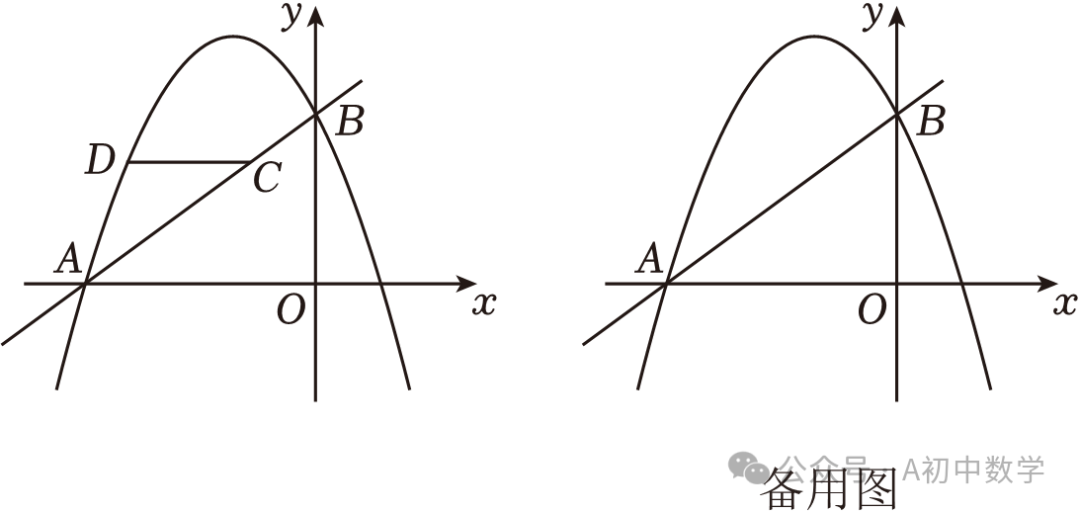
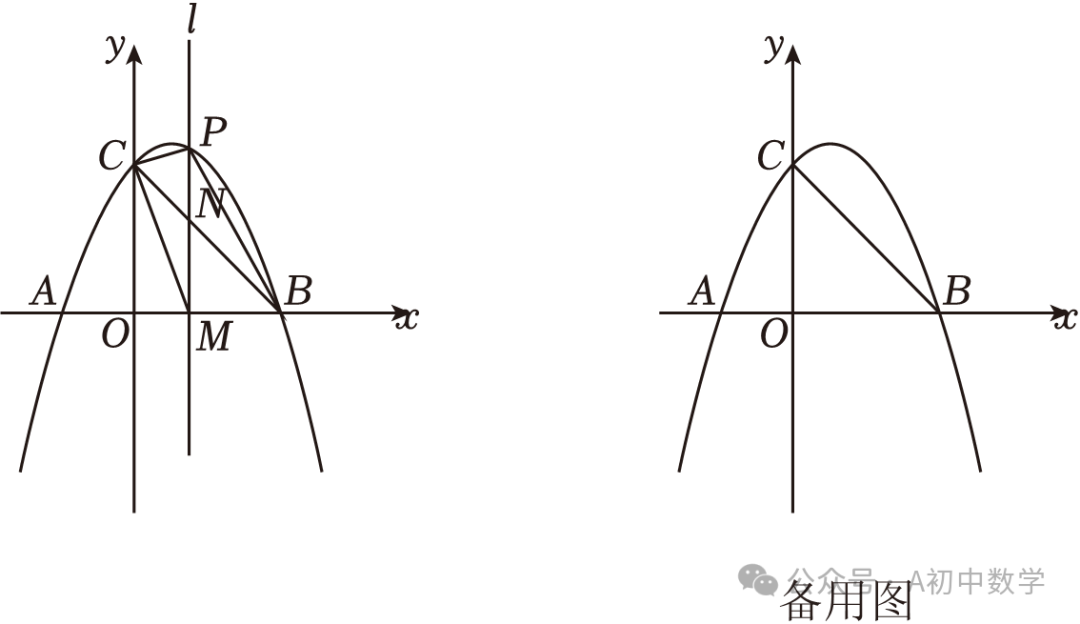
2．（2023•朝阳）如图，在平面直角坐标系中，抛物线y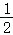＝﹣x²+bx+c与x轴分别交于点A（﹣2，0），B（4，0），与y轴交于点C，连接BC．

（1）求抛物线的解析式；

（2）如图1，点P是第一象限内抛物线上的一个动点，过点P作直线l⊥x轴于点M（m，0），交BC于点N，连接CM，PB，PC．△PCB的面积记为S₁，△BCM的面积记为S₂，当S₁＝S₂时，求m的值；

（3）在（2）的条件下，点Q在抛物线上，直线MQ与直线BC交于点H，当△HMN与△BCM相似时，请直接写出点Q的坐标．

【中考模拟练】

1．（2024•东莞市一模）已知：在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+3与x轴交于点B，与y轴交于点C，抛物线y＝﹣x²+bx+c经过B、C两点，与x轴的另一交点为点A．

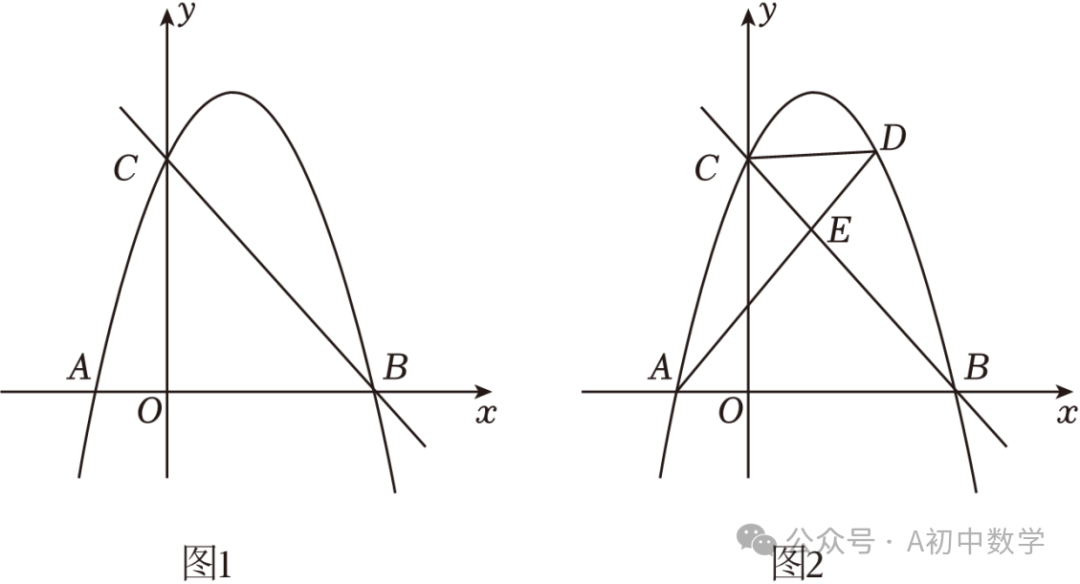
（1）如图1，求抛物线的解析式；

（2）如图2，点D为直线BC上方抛物线上一动点，连接AC、CD，设直线BC交线段AD于点E，△CDE的面积为S₁，△ACE的面积为S₂．当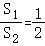时，求点D的坐标；

（3）在（2）的条件下，且点D的横坐标小于2，是否在数轴上存在一点P，使得以A、C、P为顶点的三角形与△BCD相似，如果存在，请直接写出点P的坐标；如果不存在，请说明理由．

题型四：二次函数与新定义的综合

【中考真题练】

1．（2023•南通）定义：平面直角坐标系xOy中，点P（a，b），点Q（c，d），若c＝ka，d＝﹣kb，其中k为常数，且k≠0，则称点Q是点P的“k级变换点”．例如，点（﹣4，6）是点（2，3）的“﹣2级变换点”．

（1）函数y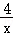＝﹣的图象上是否存在点（1，2）的“k级变换点”？若存在，求出k的值；若不存在，说明理由；

（2）动点A（t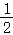，t﹣2）与其“k级变换点”B分别在直线l₁，l₂上，在l₁，l₂上分别取点（m²，y₁），（m²，y₂）．若k≤﹣2，求证：y₁﹣y₂≥2；

（3）关于x的二次函数y＝nx²﹣4nx﹣5n（x≥0）的图象上恰有两个点，这两个点的“1级变换点”都在直线y＝﹣x+5上，求n的取值范围．

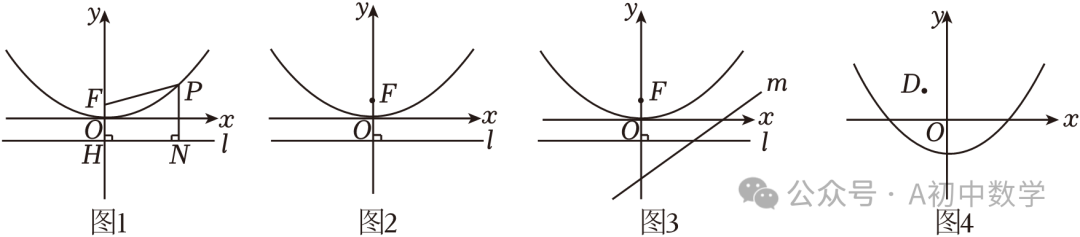
2．（2023•鄂州）某数学兴趣小组运用《几何画板》软件探究y＝ax²（a＞0）型抛物线图象．发现：如图1所示，该类型图象上任意一点P到定点F（0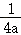，）的距离PF，始终等于它到定直线l：y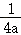＝﹣的距离PN（该结论不需要证明）．他们称：定点F为图象的焦点，定直线l为图象的准线，y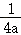＝﹣叫做抛物线的准线方程．准线l与y轴的交点为H．其中原点O为FH的中点，FH＝2OF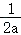＝．例如，抛物线y＝2x²，其焦点坐标为F（0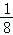，），准线方程为l：y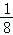＝﹣，其中PF＝PN，FH＝2OF＝．

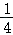【基础训练】

（1）请分别直接写出抛物线y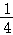＝x²的焦点坐标和准线l的方程：       ，         ；

【技能训练】

（2）如图2，已知抛物线y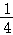＝x²上一点P（x₀，y₀）（x₀＞0）到焦点F的距离是它到x轴距离的3倍，求点P的坐标；

【能力提升】

（3）如图3，已知抛物线y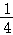＝x²的焦点为F，准线方程为l．直线m：y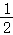＝x﹣3交y轴于点C，抛物线上动点P到x轴的距离为d₁，到直线m的距离为d₂，请直接写出d₁+d₂的最小值；

【拓展延伸】

该兴趣小组继续探究还发现：若将抛物线y＝ax²（a＞0）平移至y＝a（x﹣h）²+k（a＞0）．抛物线y＝a（x﹣h）²+k（a＞0）内有一定点F（h，k+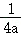），直线l过点M（h，k﹣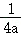）且与x轴平行．当动点P在该抛物线上运动时，点P到直线l的距离PP₁始终等于点P到点F的距离（该结论不需要证明）．例如：抛物线y＝2（x﹣1）²+3上的动点P到点F（1，）的距离等于点P到直线l：y＝的距离．

请阅读上面的材料，探究下题：

（4）如图4，点D（﹣1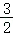，）是第二象限内一定点，点P是抛物线y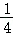＝x²﹣1上一动点．当PO+PD取最小值时，请求出△POD的面积．

【中考模拟练】

1．（2024•新吴区一模）如图，已知抛物线y＝ax²+bx（a≠0）顶点的纵坐标为﹣4，且与x轴交于点A（4，0）．作出该抛物线位于x轴下方的图象关于x轴对称的图象，位于x轴上方的图象保持不变，就得到y＝|ax²+bx|的图象，直线y＝kx（k＞0）与y＝|ax²+bx|的图象交于O、B、C三点．

（1）求a、b的值；

（2）新定义：点M（x_m，y_m）与点N（x_n，y_n）的“折线距离”为ρ（M，N）＝|x_m﹣x_n|+|y_m﹣y_n|．已知ρ（O，B）＝ρ（B，C）．

①求k的值；

②以点B为圆心、OB长为半径的⊙B交∠AOC的平分线于点D（异于点O），交x轴点E（异于点O），求ρ（D，E）的值．

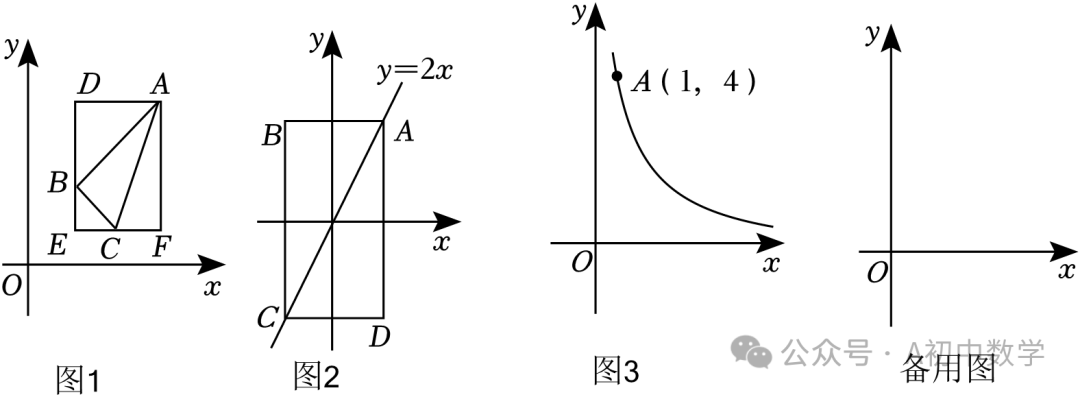
2．（2024•宝安区二模）在平面直角坐标系中，有如下定义：若某图形W上的所有点都在一个矩形的内部或边界上（该矩形的一条边平行于x轴），这些矩形中面积最小的矩形叫图形W的“美好矩形”．

例如：如图1，已知△ABC，矩形ADEF，AD∥x轴，点B在DE上，点C在EF上，则矩形ADEF为△ABC的美好矩形．

（1）如图2，矩形ABCD是函数y＝2x（﹣1≤x≤1）图象的美好矩形，求出矩形ABCD的面积；

（2）如图3，点A的坐标为（1，4），点B是函数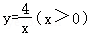图象上一点，且横坐标为m，若函数图象在A、B之间的图形的美好矩形面积为9，求m的值；

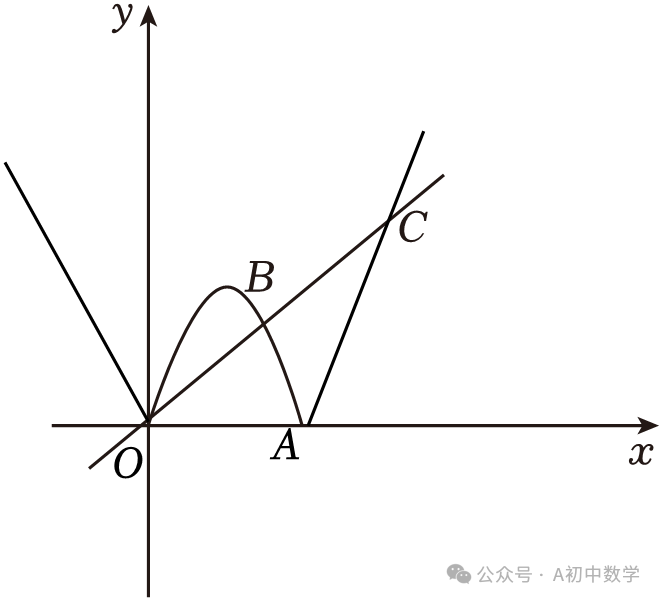
（3）对于实数a，当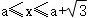时，函数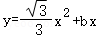图象的美好矩形恰好是面积为3，且一边在x轴上的正方形，请直接写出b的值．

由于篇幅有限，答案较长，需要参考答案的朋友们请在文末获取哦！