
秘籍02 三角形综合

概率预测 | ☆☆☆☆☆ |
题型预测 | 解答题☆☆☆☆ |
考向预测 | ①三角形全等 ②三角形相似 |

三角形综合题是全国中考常考题型。三角形是初中几何最基础的,也是中考考题必拿分题。
1.从考点频率看,三角形的综合和四边形的综合都属于高频考点,三角形综合题以考查三角形全等为主。
2.从题型角度看,以解答题为主,分值8-12分!

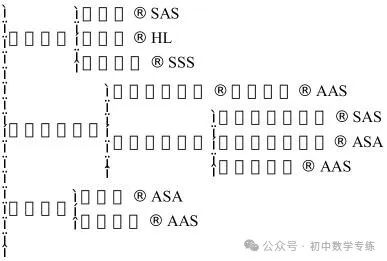
一、三角形的全等的判定思路
二、全等三角形的应用
运用全等三角形,可以证明线段相等、线段的和差倍分关系、角相等、两直线位置关系等常见的几何问题.可以适当总结证明方法.
1. 证明线段相等的方法:
(1) 证明两条线段所在的两个三角形全等.
(2) 利用角平分线的性质证明角平分线上的点到角两边的距离相等.
(3) 等式性质.
2. 证明角相等的方法:
(1) 利用平行线的性质进行证明.
(2) 证明两个角所在的两个三角形全等.
(3) 利用角平分线的判定进行证明.
(4) 同角(等角)的余角(补角)相等.
(5) 对顶角相等.
3. 证明两条线段的位置关系(平行、垂直)的方法;
可通过证明两个三角形全等,得到对应角相等,再利用平行线的判定或垂直定义证明.
4. 辅助线的添加:
(1)作公共边可构造全等三角形;
(2)倍长中线法;
(3)作以角平分线为对称轴的翻折变换全等三角形;
(4)利用截长(或补短)法作旋转变换的全等三角形.
5. 证明三角形全等的思维方法:
(1)直接利用全等三角形判定和证明两条线段或两个角相等,需要我们敏捷、快速地发现两条线段和两个角所在的两个三角形及它们全等的条件.
(2)如果要证明相等的两条线段或两个角所在的三角形全等的条件不充分时,则应根据图形的其它性质或先证明其他的两个三角形全等以补足条件.
(3)如果现有图形中的任何两个三角形之间不存在全等关系,此时应添置辅助线,使之出现全等三角形,通过构造出全等三角形来研究平面图形的性质.
三、三角形的相似
相似三角形的判定:
判定方法(一):平行于三角形一边的直线和其他两边相交,所构成的三角形和原三角形相似.
判定方法(二):如果两个三角形的三组对应边的比相等,那么这两个三角形相似.
判定方法(三):如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
判定方法(四):如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
相似三角形的性质:
(1)相似三角形的对应角相等,对应边的比相等;
(2)相似三角形中的重要线段的比等于相似比;
相似三角形对应高,对应中线,对应角平分线的比都等于相似比.

例1、(2021·兰州)如图,点 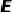 ,
, 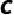 在线段
在线段 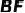 上,
上, 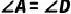 ,
, 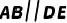 ,
, 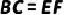 ,求证:
,求证: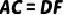 .
.
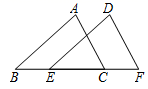
例2、(2021·宜宾)如图,已知OA=OC,OB=OD,∠AOC=∠BOD.求证:△AOB≌△COD.
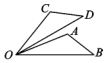
例3、(2021·西藏)如图,AB∥DE,B,C,D三点在同一条直线上,∠A=90°,EC⊥BD,且AB=CD.求证:AC=CE.
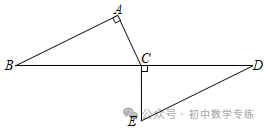
例4、(2021·南充)如图, 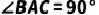 ,AD是
,AD是  内部一条射线,若
内部一条射线,若 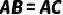 ,
, 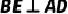 于点E,
于点E, 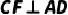 于点F.求证:
于点F.求证: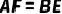 .
.
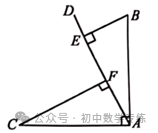
例5、(2021·陕西)如图, 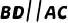 ,
, 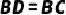 ,点
,点 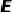 在
在 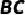 上,且
上,且 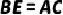 .求证:
.求证: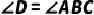 .
.
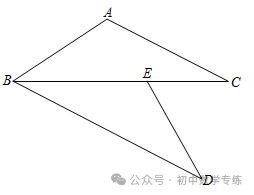
例6、如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
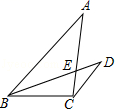
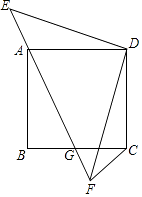 例7、如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
例7、如图示,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
①求证:△DAE≌△DCF;
②求证:△ABG∽△CFG.
例8、(2020·凉山州)如图,△ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少mm.

直接证明全等条件不足时,注意观察图形,可以通过以下方向思思考:
①角平分线做点到两边的垂线;②垂直平分线,连接两端点;③平行线或垂线的性质的性质;④特殊四边形的性;⑤等腰三角形(等边三角形)的性质。另外,相似的题目一般与结合综合结合,例如:几何动点和圆内综合
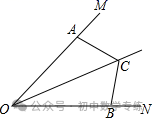
1.如图,已知OC平分∠MON,点A、B分别在射线OM,ON上,且OA=OB.
求证:△AOC≌△BOC.
2.已知:如图,在正方形 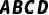 中,对角线
中,对角线 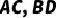 相交于点O,点
相交于点O,点 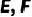 分别是边
分别是边 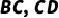 上的点,且
上的点,且 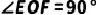 .
.
求证: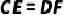 .
.

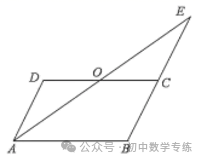
3.已知:如图,在 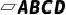 中,点O是
中,点O是 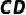 的中点,连接
的中点,连接 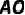 并延长,交
并延长,交 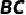 的延长线于点E,求证:
的延长线于点E,求证: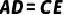 .
.
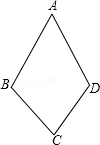
4.已知:如图,AB=AD,BC=DC.求证:∠B=∠D.
5.已知菱形ABCD,E,F分别为菱形外的两点,且E,C,F三点共线,EF交AB于G,连接AE,DE,DF,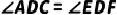 .求证:
.求证: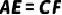 .
.
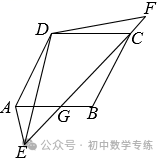
 1.(2022·天河模拟)如图,已知AB∥DE,AB = DE,B,E,C,F在同一条直线上,且BE = CF.
1.(2022·天河模拟)如图,已知AB∥DE,AB = DE,B,E,C,F在同一条直线上,且BE = CF.
求证∶△ABC≌△DEF.
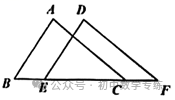
2.(2022·济南模拟)如图,四边形ABCD是平行四边形,E为BC的中点,连接AE交DC延长线于点F.求证:DC=CF.
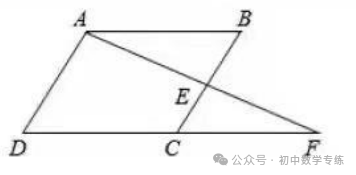
3.(2021·福建模拟)如图,点  在正方形
在正方形 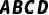 的边
的边 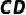 上,
上, 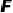 为
为  延长线上一点,且
延长线上一点,且 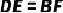 ,连接
,连接  ,
,  .求证:
.求证: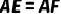 .
.
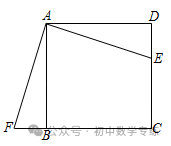
4.(2021·莲湖模拟)如图, 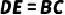 ,
, 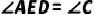 ,
, 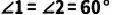 .求证:
.求证: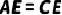 .
.
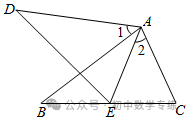
5.(2021·章丘模拟)如图,AB∥CD,E、F分别为AB、CD上的点,且EC∥BF,连接AD,分别与EC、BF相交于点G、H,若AB=CD,求证:AG=DH.
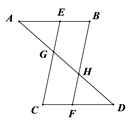
6.(2021·厦门模拟)如图,在菱形ABCD中,E、F分别在边BC、CD上,且CE=CF,
求证:∠BAE=∠DAF.
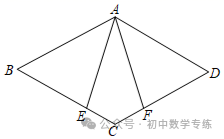
7.(2021·官渡模拟)风筝起源于中国,至今已有2300多年的历史.如图,在小明设计的“风筝”图案中,已知 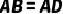 ,
, 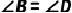 ,
, 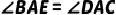 .求证:
.求证: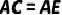 .
.
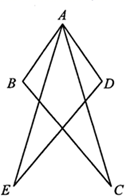
8.(2021·天桥模拟)如图,在矩形ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,DF⊥AC于点F. 求证:AE=DF.
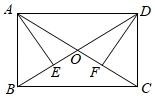
9.(2021·南昌模拟)如图,点D在△ABC的边AB上,AC2=AD•AB,求证:△ACD∽△ABC.
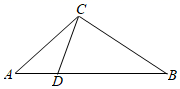
10.(2021·汝阳模拟)如图, 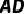 与
与 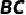 交于
交于 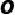 点,
点, 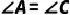 ,
, 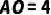 ,
, 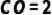 ,
, 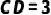 ,求
,求  的长.
的长.

11.(2020·临潭模拟)如图,在△ABC中,AD=DB,∠1=∠2.求证:△ABC∽△EAD.
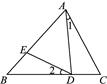
12.(2022·重庆模拟)在 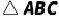 中,
中, 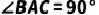 ,点O是斜边
,点O是斜边 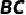 上的一点,连接
上的一点,连接 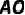 ,点D是
,点D是 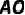 上一点,过点D分别作
上一点,过点D分别作 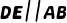 ,
, 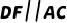 ,交
,交 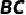 于点E、F.
于点E、F.
(1)如图1,若点O为斜边 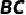 的中点,求证:点O是线段
的中点,求证:点O是线段  的中点.
的中点.
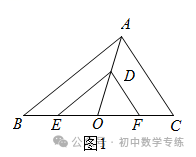
(2)如图2,在(1)的条件下,将 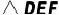 绕点O顺时针旋转任意一个角度,连接
绕点O顺时针旋转任意一个角度,连接 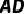 ,
, 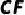 ,请写出线段
,请写出线段 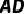 和线段
和线段 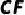 的数量关系,并说明理由.
的数量关系,并说明理由.
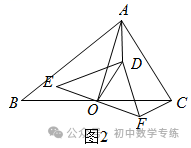
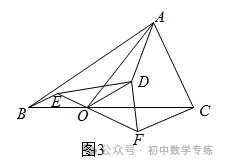
(3)如图3,若点O是斜边 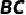 的三等分点,且靠近点
的三等分点,且靠近点 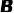 ,当
,当 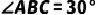 时,将
时,将 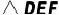 绕点O顺时针旋转任意一个角度,连接
绕点O顺时针旋转任意一个角度,连接 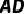 、
、 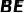 、
、 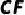 ,请求出
,请求出 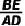 的值.
的值.
13.(2022·威海模拟)如图,已知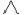 ABC内接于⊙O,AB是⊙O的直径,∠CAB的平分线交BC于点D,交⊙O于点E,连接EB,作∠BEF=∠CAE,交AB的延长线于点F.
ABC内接于⊙O,AB是⊙O的直径,∠CAB的平分线交BC于点D,交⊙O于点E,连接EB,作∠BEF=∠CAE,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若BF=10,EF=20,求⊙O的半径和AD的长.







