

秘籍04 圆的综合 
概率预测 | ☆☆☆☆☆ |
题型预测 | 解答题☆☆☆☆☆ |
考向预测 | ①有关圆的证明题 ②有关圆的计算 |

圆的综合题是全国中考的热点内容,更是全国中考的必考内容!圆作为一个载体,常与三角形、四边形结合,难度系数中等。
1.从考点频率看,圆是高频考点,中考对圆的知识点考查,综合能力要求极高!
2.从题型角度看,以解答题为主,分值10分左右!

圆常见辅助线的作法
1:连接半径,构造等腰三角形
在圆的相关题目中,不要忽略隐含的已知条件,我们通常可以连接半径构造等腰三角形,从而利用等腰三角形的性质及圆中的相关定理。
2:遇弦添加弦心距或半径
根据垂径定理,连半径,可以构造直角三角形。设未知数,利用勾股定理列方程,求线段的长度。
3:构造同弧或等弧所对的圆心角或圆周角解题
在同一圆中,同弧或等弧所对的圆周角等于圆心角的一半。
在同一圆中,同弧或等弧所对的圆周角相等。
4:构造直角或直径
直径所对的圆周角是90°。
5:切线的性质有关的辅助线——添加过切点的半径
利用切线性质,可得半径与切线垂直
6:切线的判定有关的辅助线
(1)有公共点,连半径,证垂直。(2)无公共点,作垂直,证明与半径相等。
7:与三角形内切圆有关的辅助线
遇到三角形的内切圆时,连接内心与三角形各顶点,利用内心的性质进行有关计算与证明。

中考圆的综合题常见的隐含条件:①同圆所有的半径都相等;②直径所对的圆周角相等;③同弧或等弧所对的圆周角相等。有关圆的解答题综合性特别强,会用到初中阶段所学所有几何知识点,如果所有方法都尝试不行,记得用相似,对应边成比例。

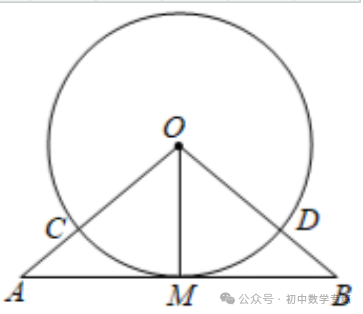
例1、如图, 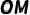 是
是 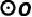 的半径,过点M作
的半径,过点M作 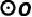 的切线
的切线  ,且
,且 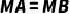 ,
,  ,
,  分别交
分别交  于点C,D,求证:
于点C,D,求证: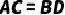
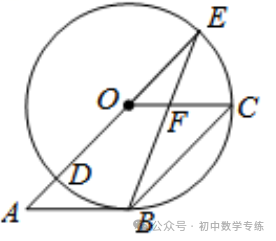
例2、如图,四边形 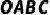 是平行四边形,以点
是平行四边形,以点 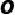 为圆心,
为圆心, 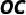 为半径的
为半径的 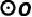 与
与  相切于点
相切于点 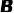 ,与
,与 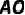 相交于点
相交于点 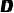 ,
, 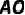 的延长线交
的延长线交 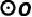 于点
于点 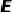 ,连接
,连接  交
交 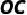 于点
于点 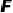 ,求
,求 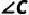 和
和 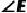 的度数.
的度数.
例3、如图, 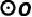 的直径
的直径  交弦(不是直径)
交弦(不是直径) 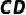 于点P,且
于点P,且  .求证:
.求证: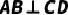 .
.

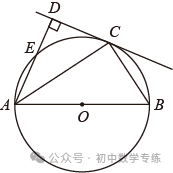
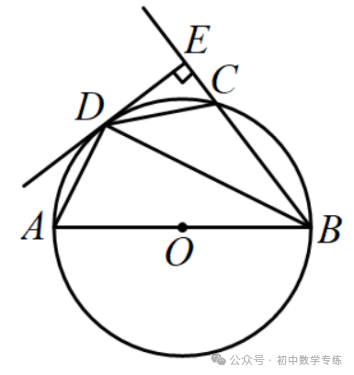
例4、(2021·南通)如图,  为
为 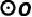 的直径,C为
的直径,C为 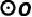 上一点,弦
上一点,弦  的延长线与过点C的切线互相垂直,垂足为D,
的延长线与过点C的切线互相垂直,垂足为D, 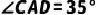 ,连接
,连接 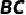 .
.
(1)求 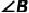 的度数;
的度数;
(2)若 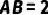 ,求
,求  的长.
的长.
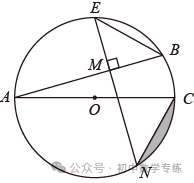
例5、(2021·安顺)如图,在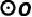 中,AC为
中,AC为 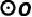 的直径, AB为
的直径, AB为 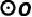 的弦,点 E 是
的弦,点 E 是  的中点,过点 E 作 AB 的垂线,交 AB 于点 M ,交
的中点,过点 E 作 AB 的垂线,交 AB 于点 M ,交  于点 N ,分别连接 EB , CN .
于点 N ,分别连接 EB , CN .
(1) 与
与  的数量关系是 ;
的数量关系是 ;
(2)求证: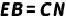 ;
;
(3)若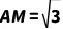 ,
, 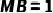 ,求阴影部分图形的面积.
,求阴影部分图形的面积.
例6、(2021·桂林)如图,四边形ABCD中,∠B=∠C=90°,点E为BC中点,AE⊥DE于点E.点O是线段AE上的点,以点O为圆心,OE为半径的⊙O与AB相切于点G,交BC于点F,连接OG.
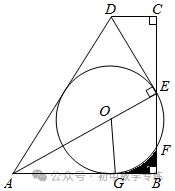
(1)求证:△ECD∽△ABE;
(2)求证:⊙O与AD相切;
(3)若BC=6,AB=3 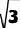 ,求⊙O的半径和阴影部分的面积.
,求⊙O的半径和阴影部分的面积.
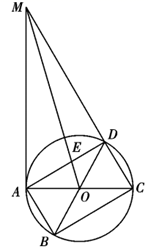
例7、(2021·绵阳)如图,四边形 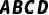 是⊙
是⊙ 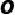 的内接矩形,过点
的内接矩形,过点 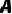 的切线与
的切线与 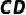 的延长线交于点
的延长线交于点 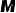 ,连接
,连接 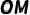 与
与 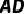 交于点
交于点 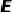 ,
, 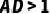 ,
, 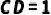 .
.
(1)求证: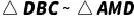 ;
;
(2)设 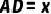 ,求
,求 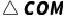 的面积(用
的面积(用 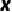 的式子表示);
的式子表示);
(3)若 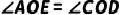 ,求
,求  的长.
的长.
例8、(2021·毕节)如图, 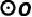 是
是 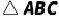 的外接圆,点E是
的外接圆,点E是 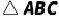 的内心,AE的延长线交BC于点F,交
的内心,AE的延长线交BC于点F,交  于点D,连接BD,BE.
于点D,连接BD,BE.
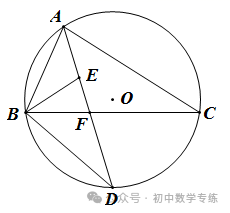
(1)求证: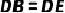 ;
;
(2)若 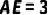 ,
, 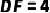 ,求DB的长.
,求DB的长.
 圆的题目总如果出现三角函数,基本都与三角形相似产生关系,以此为着手点,寻求题目突破。
圆的题目总如果出现三角函数,基本都与三角形相似产生关系,以此为着手点,寻求题目突破。
1.(2021·贵港)如图,⊙O是 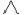 ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.
ABC的外接圆,AD是⊙O的直径,F是AD延长线上一点,连接CD,CF,且∠DCF=∠CAD.
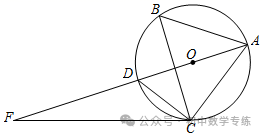
(1)求证:CF是⊙O的切线;
(2)若cosB= 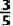 ,AD=2,求FD的长.
,AD=2,求FD的长.
2.(2021·资阳)如图,在△ABC中,AB=AC,DE⊥AC交BA的延长线于点E,交AC于点F.
(1) 求证:DE是⊙O的切线;
(2) 若AC=6,tanE= 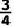 ,求AF的长.
,求AF的长.
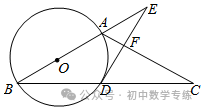
 1.(2022·威海模拟)如图,已知
1.(2022·威海模拟)如图,已知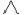 ABC内接于⊙O,AB是⊙O的直径,∠CAB的平分线交BC于点D,交⊙O于点E,连接EB,作∠BEF=∠CAE,交AB的延长线于点F.
ABC内接于⊙O,AB是⊙O的直径,∠CAB的平分线交BC于点D,交⊙O于点E,连接EB,作∠BEF=∠CAE,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若BF=10,EF=20,求⊙O的半径和AD的长.
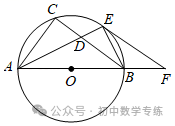
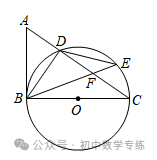
2.(2022·云南模拟)如图,点C在以AB为直径的⊙O上,BD平分∠ABC交⊙O于点D,过D作BC的垂线,垂足为E.
(1)求证:DE与⊙O相切;
(2)若AB=5,BE=4,求BD的长;
(3)请用线段AB、BE表示CE的长,并说明理由.
3.(2022·蚌埠模拟)如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AB于点D,点E为BC的中点,连接OD、DE.

(1)求证:OD⊥DE.
(2)若∠BAC=30°,AB=8,求阴影部分的面积.
4.(2022·中山模拟)如图,在△ABC中,以BC为直径的⊙O交AC于点D,点E在⊙O上,且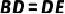 ,连接BE交AC于点F,已知BA=BF.
,连接BE交AC于点F,已知BA=BF.
(1)求证:AB是⊙O的切线;
(2)若AF=6,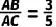 ,求⊙O的直径.
,求⊙O的直径.
5.(2022·坪山模拟)如图,在Rt△ABC中,∠ACB=90°,点D是边AB上一点,以BD为直径的⊙O与AC交于点E,连接DE并延长交BC的延长线于点F,且BF=BD.
(1)求证:AC为⊙O的切线;
(2)若CF=1,tan∠EDB=2,求⊙O的半径.
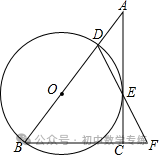
6.(2022·亳州模拟)如图,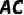 为⊙O的直径,过点
为⊙O的直径,过点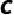 的切线与弦
的切线与弦 的延长线交于点
的延长线交于点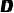 为半径,
为半径,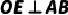 于点
于点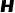 ,连接
,连接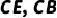 .
.
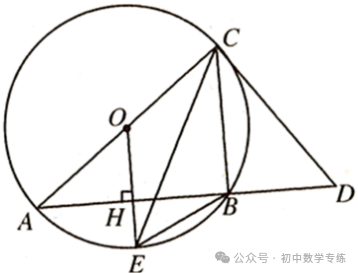
(1)求证: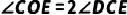 ;
;
(2)若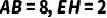 ,求
,求 的长.
的长.
7.(2022·合肥模拟)如图,点A,C是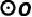 上的点,且
上的点,且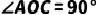 ,过点A作
,过点A作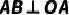 ,连接BC交
,连接BC交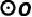 于点D,点D是BC的中点.
于点D,点D是BC的中点.
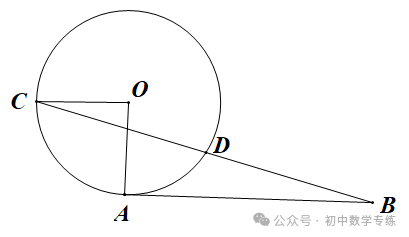
(1)求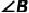 的度数;
的度数;
(2)求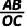 的值.
的值.
8.(2022·安徽模拟)如图,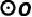 的半径为1,A、B、C是
的半径为1,A、B、C是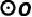 上的三个点,点P在劣弧AB上,
上的三个点,点P在劣弧AB上,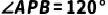 ,PC平分
,PC平分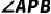 .
.
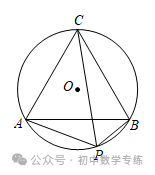
(1)求证: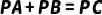 ;
;
(2)当点P位于什么位置时, 的面积最大?求出最大面积.
的面积最大?求出最大面积.
9.(2021·铁岭模拟)如图,半径为7的 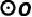 上有一动点
上有一动点 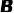 ,点
,点 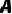 为半径
为半径  上一点,且
上一点,且  最大为10,以
最大为10,以  为边向外作正方形
为边向外作正方形 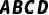 ,连接
,连接 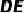 .
.
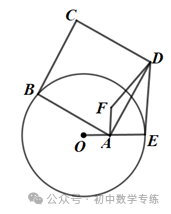
(1)请直接写出 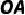 的长;
的长;
(2)过点 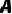 作
作 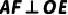 ,且
,且 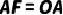 ,连接
,连接 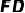 ,在点
,在点 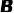 的运动过程中,
的运动过程中, 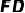 的长度会发生变化吗?变化请说明理由,不变化请求出
的长度会发生变化吗?变化请说明理由,不变化请求出 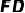 的长;
的长;
(3)当点A,B,F三点在一条直线上时,请直接写 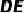 的长;
的长;
(4)请直接写出 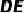 的最大值和最小值.
的最大值和最小值.





