滨州市2023年初中学业水平考试数学试卷
温馨提示:
1.本试卷分第Ⅰ卷和第Ⅱ卷两部分,共4页,满分120分,考试用时120分钟.考试结束后,将试题卷和答题卡一并交回.
2.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在试题卷和答题卡规定的位置上.
3.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案标号,答案不能答在试题卷上;
4.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试题卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.
第Ⅰ卷(选择题 共24分)
一、选择题:本大题共8个小题;在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,用2B铅笔把答题卡上对应题目的答案标号涂黑.每小题涂对得3分,满分24分.
1. ﹣3的相反数是( )
A. B. C. D.
2. 下列计算,结果正确的是( )
A. B.
C. D.
3. 如图所示摆放的水杯,其俯视图为( )
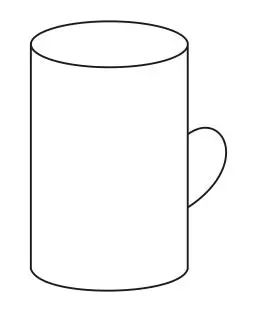
A. 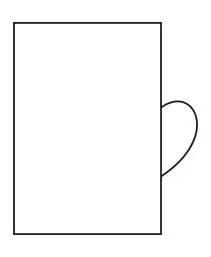 B.
B.  C.
C. 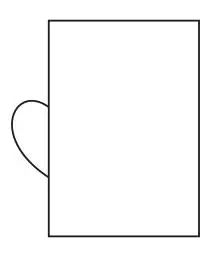 D.
D. 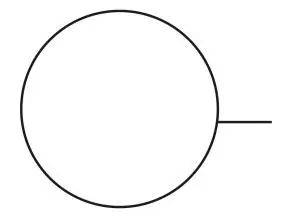
4. 一元二次方程根的情况为( )
A. 有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.不能判定
5.由化学知识可知,用表示溶液酸碱性的强弱程度,当时溶液呈碱性,当时溶液呈酸性.若将给定的溶液加水稀释,那么在下列图象中,能大致反映溶液的与所加水的体积之间对应关系的是( )
A. 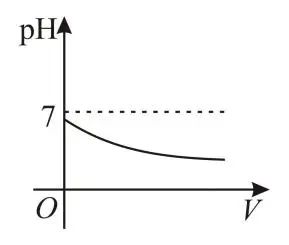 B.
B. 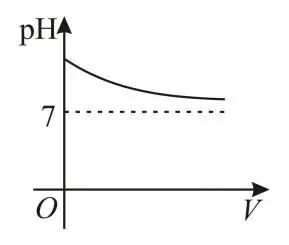
C. 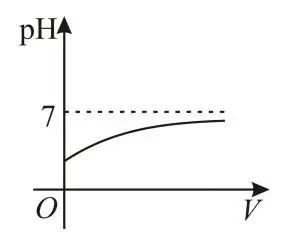 D.
D. 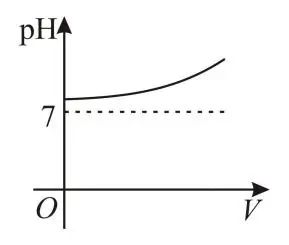
6. 在某次射击训练过程中,小明打靶次的成绩(环)如下表所示:
靶次 | 第次 | 第次 | 第次 | 第次 | 第次 | 第次 | 第次 | 第次 | 第次 | 第次 |
成绩(环) |
则小明射击成绩的众数和方差分别为( )
A. 和 B.和
C.和 D.和
7.如图,某玩具品牌标志由半径为的三个等圆构成,且三个等圆相互经过彼此的圆心,则图中三个阴影部分的面积之和为( )
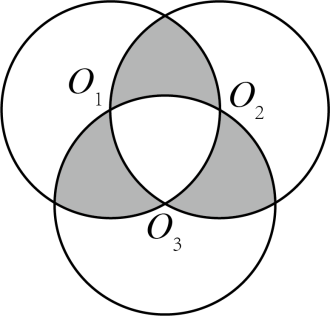
A. B.
C. D.
8.已知点是等边边上的一点,若,则在以线段为边的三角形中,最小内角的大小为( )
A. B. C. D.
第Ⅱ卷(非选择题 共96分)
二、填空题:本大题共8个小题,每小题3分,满分24分.
9. 计算的结果为___________.
10. 一块面积为的正方形桌布,其边长为___________.
11. 不等式组的解集为___________.
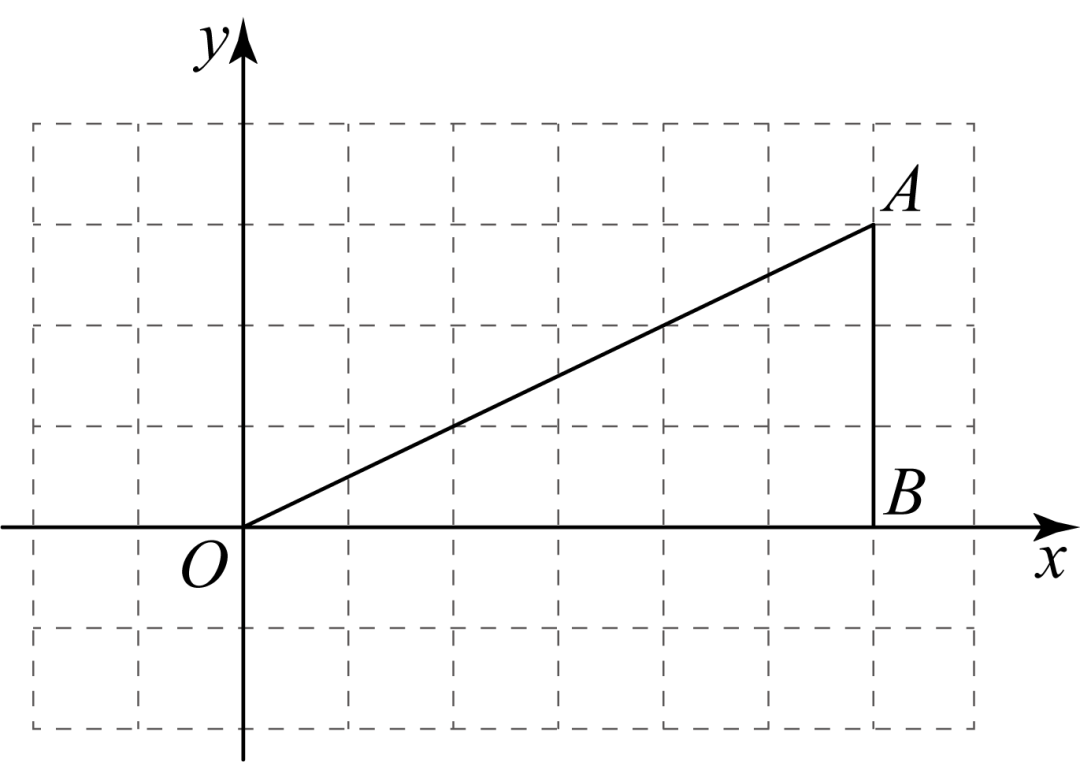
12.如图,在平面直角坐标系中,的三个顶点坐标分别为.若将向左平移3个单位长度得到,则点A的对应点的坐标是___________.
13. 同时掷两枚质地均匀骰子,则两枚骰子点数之和等于7的概率是___________.
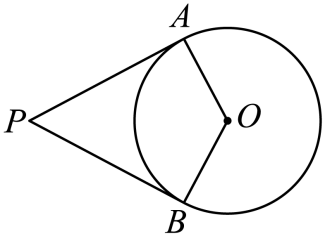
14.如图,分别与相切于两点,且.若点是上异于点的一点,则的大小为___________.
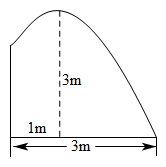
15.要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心,水管长度应为____________.
16.如图,矩形对角线相交于点,点分别是线段上的点.若,则的长为___________.
三、解答题:本大题共6个小题,满分72分.解答时请写出必要的演推过程.
17.中共中央办公厅、国务院办公厅印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》中,对学生每天的作业时间提出明确要求:“初中书面作业平均完成时间不超过90分钟”.为了更好地落实文件精神,某县对辖区内部分初中学生就“每天完成书面作业的时间”进行了随机调查,为便于统计学生每天完成书面作业的时间(用t表示,单位h)状况设置了如下四个选项,分别为A:,B:,C:,D:,并根据调查结果绘制了如下两幅不完整的统计图.
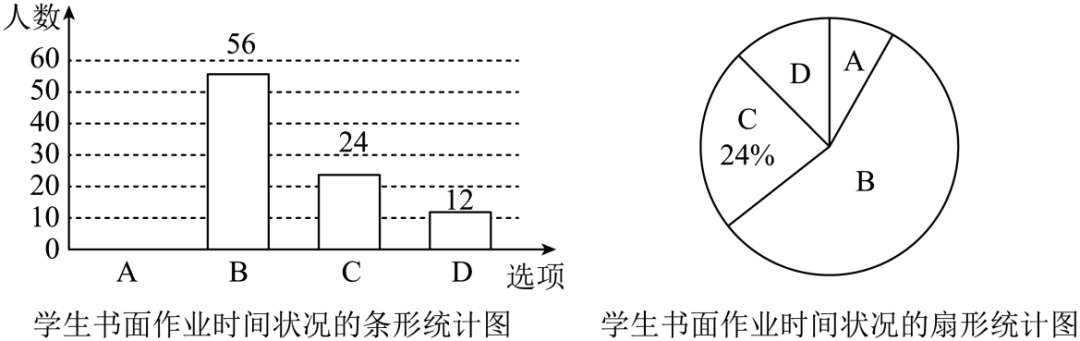
请根据以上提供的信息解答下列问题:
(1)此次调查,选项A中的学生人数是多少?
(2)在扇形统计图中,选项D所对应的扇形圆心角的大小为多少?
(3)如果该县有15000名初中学生,那么请估算该县“每天完成书面作业的时间不超过90分钟”的初中学生约有多少人?
(4)请回答你每天完成书面作业的时间属于哪个选项,并对老师的书面作业布置提出合理化建议.
18. 先化简,再求值:,其中满足.
19. 如图,直线为常数与双曲线(为常数)相交于,两点.
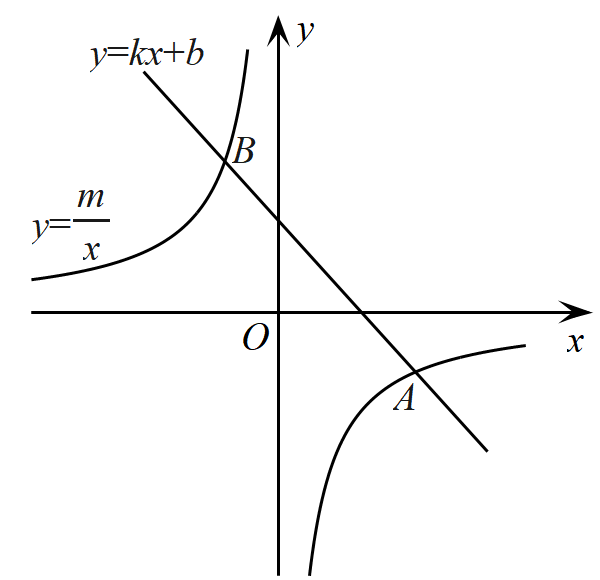
(1)求直线的解析式;
(2)在双曲线上任取两点和,若,试确定和的大小关系,并写出判断过程;
(3)请直接写出关于的不等式的解集.
20. (1)已知线段,求作,使得;(请用尺规作图,保留作图痕迹,不写作法.)
(2)求证:直角三角形斜边上的中线等于斜边的一半.(请借助上一小题所作图形,在完善的基础上,写出已知、求证与证明.)
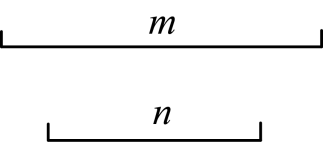
21.如图,在平面直角坐标系中,菱形的一边在轴正半轴上,顶点的坐标为,点是边上的动点,过点作交边于点,作交边于点,连接.设的面积为.
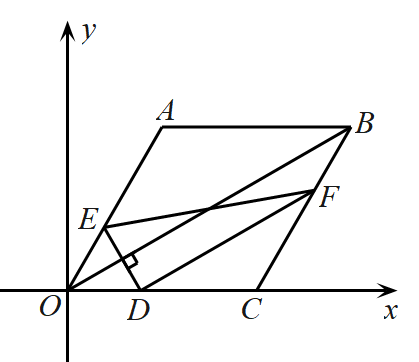
(1)求关于的函数解析式;
(2)当取何值时,值最大?请求出最大值.
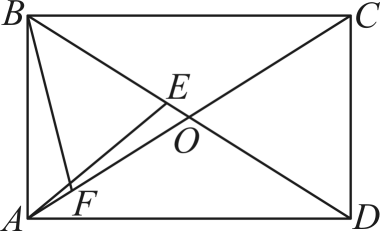
22. 如图,点是的内心,的延长线与边相交于点,与的外接圆相交于点.
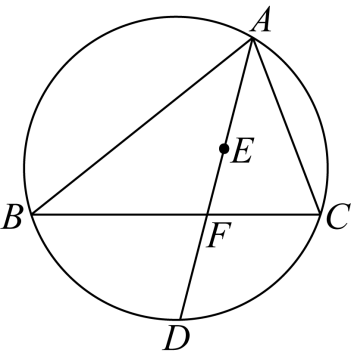
(1)求证:;
(2)求证:;
(3)求证:;
(4)猜想:线段三者之间存在的等量关系.(直接写出,不需证明.)
下载
关注本公众号
并在对话界面回复
“231947”
自动获取试题和答案下载链接
分享是一种美德,点赞是一种支持
由于历年中考真题信息量巨大,短时间内无法全部编辑发布在公众号里,为了满足各位考生和家长的需求,可以添加微信,添加时备注“爱都公众号”,老师在方便的时间内第一时间分享给你!
分享“朋友圈”、点亮 “在看”可以获取多套真题
2023年全国数学中考真题试卷免费送

扫一扫上面二维码加“爱都数理化”微信,获取更多真题
获取多套真题只能通过微信或QQ发送
-aidu2021-
资料来源于互联网
如有侵权,请及时告知,我将立即删除
整编:东方龙
爱都,不是名师的聚集地
爱都,只是知识的搬运工
渴望超越,从爱都出发
可以点“在看”给我一朵  吗?
吗?

爱读书 爱学习
QQ:3188982078






