
一、单选题
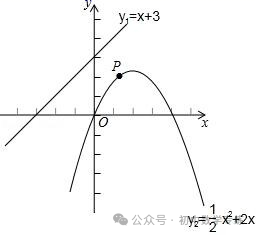
1.(2020·乐陵市实验中学九年级月考)已知,平面直角坐标系中,直线 y1=x+3与抛物线y2=﹣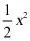 +2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()
+2x 的图象如图,点P是 y2 上的一个动点,则点P到直线 y1 的最短距离为()

A.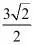 B.
B.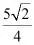
 C.
C.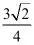 D.
D.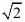
2.(2019·广西中考模拟)若反比例函数y=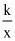 的图象经过点(2,3),则它的图象也一定经过的点是( )
的图象经过点(2,3),则它的图象也一定经过的点是( )
A.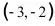 B.
B.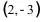
 C.
C.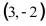 D.
D.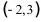
3.(2021·天津)已知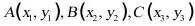 是反比例函数
是反比例函数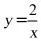
 上的三点,若
上的三点,若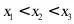 ,则下列关系式不正确的是 ( )
,则下列关系式不正确的是 ( )
A.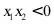 B.
B.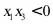
 C.
C.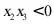 D.
D.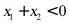
4.(2020·北京市陈经纶中学九年级月考)在平面直角坐标系xOy中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是( )
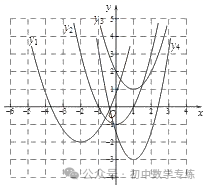

A.y1 B.y2 C.y3 D.y4
5.(2020·全国九年级课时练习)下列函数中,当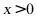
 时
时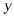 随
随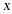 的增大而增大的是( )
的增大而增大的是( )
A.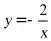 B.
B.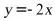
 C.
C.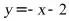 D.
D.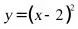
6.(2019·山西)一次函数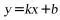 的图象经过点
的图象经过点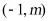
 和
和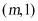 ,其中
,其中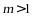 ,则k,b的取值范围是( )
,则k,b的取值范围是( )
A.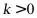 且
且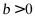 B.
B.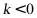 且
且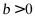
 C.
C.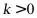 且
且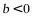 D.
D.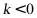 且
且
7.(2021·全国九年级专题练习)若一次函数y=kx+b的图象经过第一、二、四象限,则一次函数y=bx+k的图象大致是( )
A.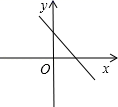 B.
B.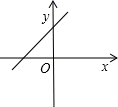
 C.
C.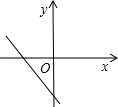 D.
D.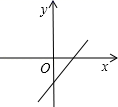
8.(2019·中山市坦洲中学中考模拟)小刚从家去学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车匀速行驶一段时后到达学校,小刚从家到学校行驶路程s(单位:m)与时间r(单位:min)之间函数关系的大致图象是( )
A.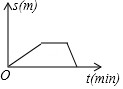
 B.
B.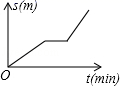
C.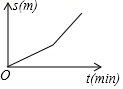
 D.
D.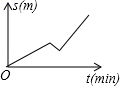
二、填空题
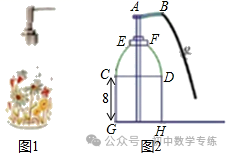
9.(2021·全国九年级期末)小林家的洗手台面上有一瓶洗手液(如图1),当手按住顶部A下压时(如图2),洗手液瞬间从喷口B流出,已知瓶子上部分的
 和
和 的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.
的圆心分别为D,C,下部分的视图是矩形CGHD,GH=10cm,GC=8cm,点E到台面GH的距离为14cm,点B距台面GH的距离为16cm,且B,D,H三点共线.如果从喷口B流出的洗手液路线呈抛物线形,且该路线所在的抛物线经过C.E两点,接洗手液时,当手心O距DH的水平距离为2cm时,手心O距水平台面GH的高度为_____cm.

10.(2019·天津滨海新·九年级二模)如图,一次函数y=kx+b的图象与x轴的交点坐标为(2,0),则下列说法:①y随x的增大而减小;②b>0;③关于x的方程kx+b=0的解为x=2;④不等式kx+b>0的解集是x>2.其中说法正确的有_________(把你认为说法正确的序号都填上).
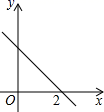

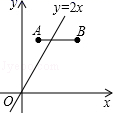
11.(2021·广东九年级专题练习)如图,在平面直角坐标系中,点A、B的坐标分别为(1,3)、(n,3),若直线y=2x与线段AB有公共点,则n的值可以为_____.(写出一个即可)

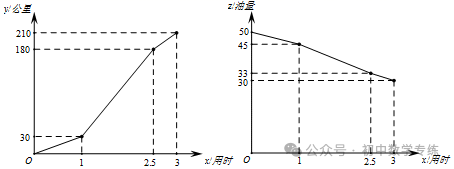
12.(2019·北京昌平·中考模拟)“五一黄金周”期间李师傅一家开车去旅游,出发前查看了油箱里有50升油,下面的两幅图分别描述了行驶里程及耗油情况,行驶130公里时,油箱里剩油量为_____升.

三、解答题
13.(2020·四川中考模拟)我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓。某市某电器商场根据民众健康需要,代理销售某种空气净化器,其进价时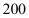 元/台。经过市场销售后发现:在一个月内,当售价是
元/台。经过市场销售后发现:在一个月内,当售价是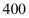 元/台时,可售出
元/台时,可售出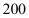
 台,且售价每降低
台,且售价每降低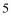 元,就可多售出
元,就可多售出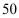 台。若供货商规定这种空气净化器售价不能低于
台。若供货商规定这种空气净化器售价不能低于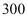 元/台,代理销售商每月要完成不低于
元/台,代理销售商每月要完成不低于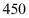 台的销售任务。
台的销售任务。
(1)求出月销售量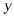
 (单位:台)与售价
(单位:台)与售价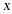 (单位:元/台)之间的函数关系式,并求出自变量
(单位:元/台)之间的函数关系式,并求出自变量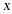 的取值范围;
的取值范围;
(2)当售价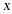
 定为多少时,商场每月销售这种空气净化器所获得的利润
定为多少时,商场每月销售这种空气净化器所获得的利润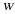 (单位:元)最大?最大利润是多少?
(单位:元)最大?最大利润是多少?
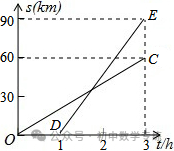
14.(2021·广西中考模拟)已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?

15.(2020·辽宁中考模拟)在一个不透明的盒子里有5个小球,分别标有数字﹣3,﹣2,﹣1,﹣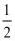
 ,﹣
,﹣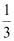 ,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
,这些小球除所标的数不同外其余都相同,先从盒子随机摸出1个球,记下所标的数,再从剩下的球中随机摸出1个球,记下所标的数.
(1)用画树状图或列表的方法求两次摸出的球所标的数之积不大于1的概率.
(2)若以第一次摸出球上的数字为横坐标,第二次摸出球上的数字为纵坐标确定一点,直接写出该点在双曲线y=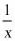 上的概率.
上的概率.
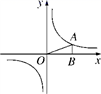
16.(2019·河北九年级专题练习)如图,已知反比例函数y=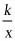 的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=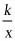 的图象上,当-3≤x≤-1时,求函数值y的取值范围.
的图象上,当-3≤x≤-1时,求函数值y的取值范围.

17.(2019·柳州市第十四中学中考模拟)已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y=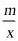 的图象的两个交点,直线AB与y轴交于点C.
的图象的两个交点,直线AB与y轴交于点C.
(1)求反比例函数和一次函数的关系式;
(2)求△AOC的面积;
(3)求不等式kx+b<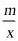 的解集(直接写出答案).
的解集(直接写出答案).
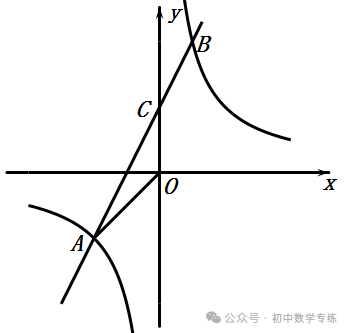

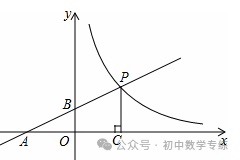
18.(2020·甘肃定西·中考模拟)如图,直线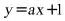 与
与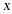 轴、
轴、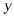 轴分别相交于
轴分别相交于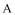 两点,与双曲线
两点,与双曲线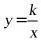

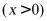 相交于点
相交于点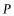 轴于点
轴于点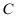 ,且
,且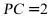 ,点
,点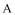 的坐标为
的坐标为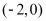 .
.

(1)求双曲线的解析式;
(2)若点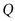 为双曲线上点
为双曲线上点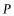 右侧的一点,且
右侧的一点,且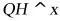 轴于
轴于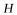
 ,当以点
,当以点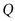 为顶点的三角形与
为顶点的三角形与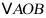 相似时,求点
相似时,求点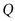 的坐标.
的坐标.
19.(2021·全国九年级专题练习)已知抛物线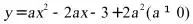 .
.
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其解析式;
(3)设点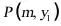
 在抛物线上,若
在抛物线上,若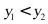 ,求m的取值范围.
,求m的取值范围.
20.(2020·浙江绍兴·九年级月考)如图,已知抛物线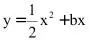
 与直线
与直线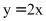 交于点O(0,0),
交于点O(0,0),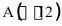 .点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
.点B是抛物线上O,A之间的一个动点,过点B分别作x轴、y轴的平行线与直线OA交于点C,E.
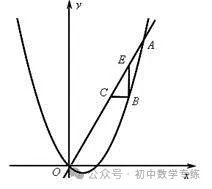

(1)求抛物线的函数解析式;
(2)若点C为OA的中点,求BC的长;
(3)以BC,BE为边构造条形BCDE,设点D的坐标为(m,n),求m,n之间的关系式.






