中考数学压轴题之新函数图像探究题类型二分段函数

中考数学压轴题之新函数图像探究题类型二分段函数

中考数学压轴题

新函数图像探究题

类型二、分段函数

  新函数图像探究题是近些年中考数学的一种新题型，在各地的中考数学试卷中已有出现，在近年越来越频繁地出现在全国各省市的中考数学试卷中。

  新函数图像探究题是建立在学生已经学习的正比例函数、一次函数、反比例函数和二次函数基础之上，将基本函数进行组合、变形、平移等形成新的函数，是对函数图像与性质的综合运用。

  在初中阶段的函数学习中，我们经历了“确定函数的表达式－－利用函数图象研究其性质－－运用函数解决问题”的学习过程。新函数图像的探究题的学习也是同样的过程，作出函数图像是解题的关键，在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象。

  画函数图像一般需要经历分析解析式、列表、描点、连线过程得到函数图象，一般情况下是草图，但需要抓住几个关键点和基本走势，然后通过通过观察、对比、分析探究函数图像的性质，解决问题。

  函数图像探究题作为近些年中考的新题型，注重对学生观察、分析、解决问题的能力及知识迁移和运用能力的考查，具有一定的综合性和跳跃性，在学习中需要不断去总结和思考，掌握常见类型的题目的解题思路和方法。

  函数图象性质的探究题常见问题：

  ①求自变量的取值范围：根据解析式中分式、二次根式等有意义的条件，列出不等式（组）进行求解；    

  ②描点、连线画函数图象：用平滑的曲线依次连接各点即可；

  ③写函数的相关性质：根据函数图象，从最值、增减性、对称性、最值点、特殊点等方面入手即可；

  ④函数与方程或不等式综合考查，观察函数图像求值或取值范围，理解函数图像的交点的坐标与方程的解的关系，掌握在同一坐标系中不同函数的值的大小与函数图像的位置关系是解题的关键。

  综合全国各省市往年的中考真题及模考题，整理出了新函数图像探究题一般常见的六种类型：

二、分段函数

1、若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数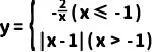的图象与性质。

列表：

描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示。

（1)如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；    

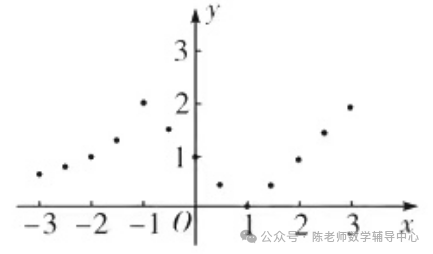
（2)研究函数并结合图象与表格，回答下列问题：

   ①点A(-5,y₁),B(-7/2，y₂),C(x₁,5/2), D(x₂, 6)在函数图象上，

   则y₁     y₂,x₁     x₂;(填“＞”，“＝”或“＜”）

   ②当函数值y=2时，求自变量x的值；

   ③在直线x=-1的右侧的函数图象上有两个不同的点P(x₃,y₃),Q(x₄,y₄),且y₃=y₄,求x₃+x₄的值；

   ④若直线y=a与函数图象有三个不同的交点，求a的取值范围。

数学陈老师:

2、生物学上研究表明：不同浓度的生长素对植物的生长速度影响不同，在一定范围内，生长素的浓度对植物的生长速度有促进作用，相反，在某些浓度范围，生长速度会变缓慢，甚至阻碍植物生长（阻碍即植物不生长，甚至枯萎），小林同学在了解到这一信息后，决定研究生长素浓度与茶树生长速度的关系，设生长素浓度为x克／升，生长速度为y毫米／天，当x超过4时，茶树的生长速度y与生长素x浓度满足关系式：y=-1/2x²+ax+c,实验数据如下表，当生长速度为0时，实验结束．    

（1)如图，建立平面直角坐标系xOy,描出表中各对对应值为坐标的点，画出该函数图象；

（2)根据上述表格，求出整个实验过程中y与x的函数关系式，并写出自变量x的取值范围；

（3)结合画出的函数图象，写出该函数的一条性质：                   ;

（4)若直线y=kx+3与上述函数图象有2个交点，则k的取值范围是：            .

数学陈老师:

3、已知函数 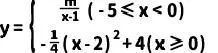，探究函数图象和性质过程如下：

（1)下表是y与x的几组值，则解析式中的m=       ,表格中的n=       .

（2)在平面直角坐标系中描出表格中各点，并画出函数图象;

（3)若A(x₁,y₁)、B(x₂,y₂)、C(x₃,y₃)为函数图象上的三个点，其中x₂+x₃＞4且－1＜x₁＜0＜x₂＜2＜x₃＜4,则y₁、y₂、y₃之间的大小关系是          ；

（4)若直线y=k+1与该函数图象有且仅有一个交点，则k的取值范围为      ．

数学陈老师:

4、小明对某市出租汽车的计费问题进行研究，他搜集了一些资料，部分信息如下：    

备注：出租车计价段里程精确到500米；出租汽车收费结算以元为单位，元以下四舍五入．

小明首先简化模型，从简单情形开始研究：

  ①只考虑白天正常行驶（无低速和等候）；

  ②行驶路程3公里以上时，计价器每500米计价1次，且每1公里中前500米计价1. 2元，后500米计价1. 1元．

下面是小明的探究过程，请补充完整：记一次运营出租车行驶的里程数为x(单位：公里），相应的实付车费为y(单位：元）。

（1)下表是y随x的变化情况

（2)在平面直角坐标系xOy中，画出当0＜x＜5.5时y随x变化的函数图象；    

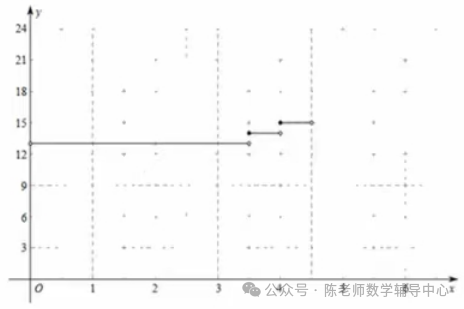
（3)一次运营行驶x公里（x＞0)的平均单价记为w(单位：元／公里），其中w=y/x.

  ①当x=3, 3.4和3.5时，平均单价依次为w₁,w₂,w₃,则w₁,w₂,w₃的大小关系

    是        （用“＜”连接）;

  ②若一次运营行驶x公里的平均单价w不大于行驶任意s(s≤x)公里的平均单价w_s ,则称这次行驶的里程数为幸运里程数．请在上图中x轴上表示出3～4(不包括端点）之间的幸运里程数x的取值范围．

点赞+关注

学习更优秀

赞赏可得电子版