中考数学:四边形压轴题综合

学而时习之，不亦说乎！

点击关注我们共同进步！

文章较长，建议收藏起来或者转发朋友圈，这样下次就更好的找到啦！

1、四边形与翻折的综合

2、四边形与旋转的综合

3、四边形与新定义的综合

4、四边形与中点的综合

电子版及答案请至文末获取哦

题型一：四边形与翻折的综合

【中考真题练】

1．（2023•西宁）折叠问题是我们常见的数学问题，它是利用图形变化的轴对称性质解决的相关问题．数学活动课上，同学们以“矩形的折叠”为主题开展了数学活动．

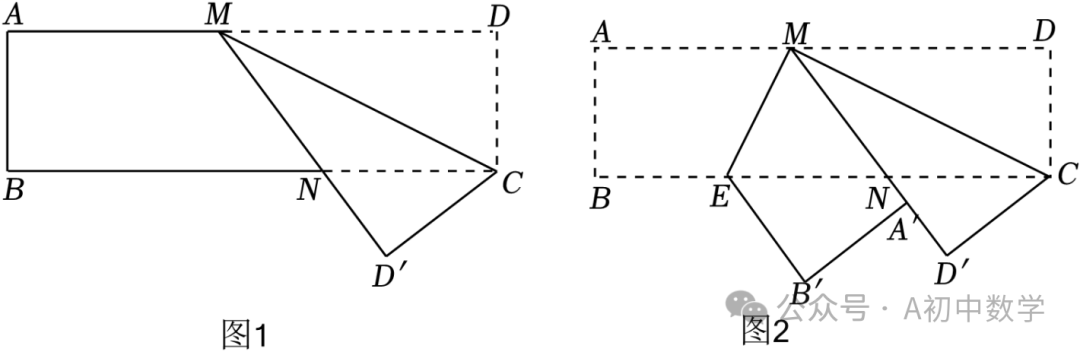
【操作】如图1，在矩形ABCD中，点M在边AD上，将矩形纸片ABCD沿MC所在的直线折叠，使点D落在点D′处，MD′与BC交于点N．

【猜想】MN＝CN．

【验证】请将下列证明过程补充完整：

∵矩形纸片ABCD沿MC所在的直线折叠，

∴∠CMD＝           ，

∵四边形ABCD是矩形，

∴AD∥BC （矩形的对边平行），

∴∠CMD＝           （                  ），

∴        ＝     （等量代换），

∴MN＝CN（          ）．

【应用】

如图2，继续将矩形纸片ABCD折叠，使AM恰好落在直线MD′上，点A落在点A′处，点B落在点B′处，折痕为ME．

（1）猜想MN与EC的数量关系，并说明理由；

（2）若CD＝2，MD＝4，求EC的长．

2．（2023•衢州）如图1，点O为矩形ABCD的对称中心，AB＝4，AD＝8，点E为AD边上一点（0＜AE＜3），连结EO并延长，交BC于点F．四边形ABFE与A′B′FE关于EF所在直线成轴对称，线段B′F交AD边于点G．

（1）求证：GE＝GF．

（2）当AE＝2DG时，求AE的长．

（3）令AE＝a，DG＝b．

①求证：（4﹣a）（4﹣b）＝4．

②如图2，连结OB′，OD，分别交AD，B′F于点H，K．记四边形OKGH的面积为S₁，△DGK的面积为S₂，当a＝1时，求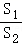的值．

3．（2023•烟台）【问题背景】

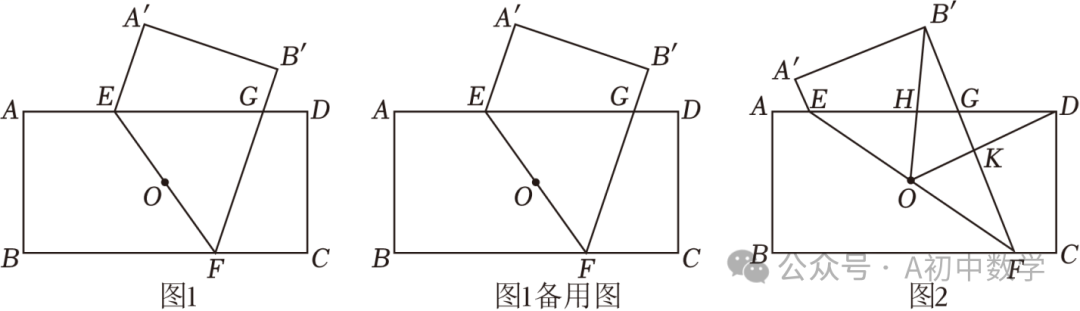
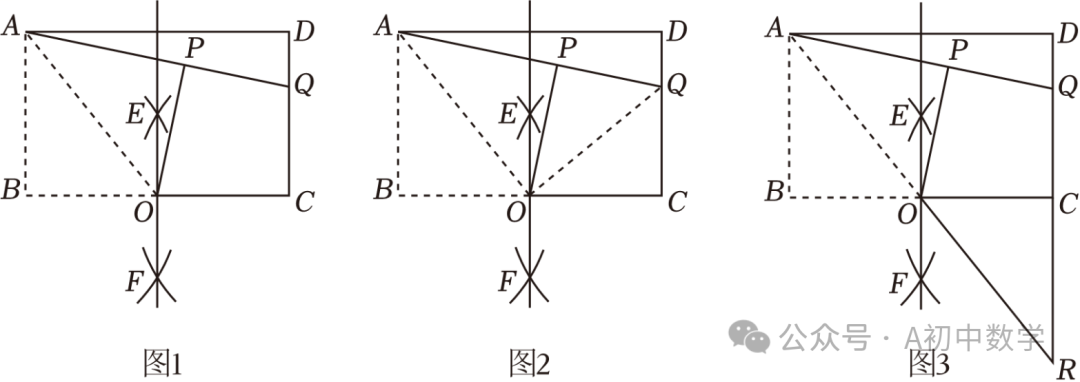
如图1，数学实践课上，学习小组进行探究活动，老师要求大家对矩形ABCD进行如下操作：①分别以点B，C为圆心，以大于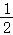BC的长度为半径作弧，两弧相交于点E，F，作直线EF交BC于点O，连接AO；②将△ABO沿AO翻折，点B的对应点落在点P处，作射线AP交CD于点Q．

【问题提出】

在矩形ABCD中，AD＝5，AB＝3，求线段CQ的长；

【问题解决】

经过小组合作、探究、展示，其中的两个方案如下：

方案一：连接OQ，如图2．经过推理、计算可求出线段CQ的长；

方案二：将△ABO绕点O旋转180°至△RCO处，如图3．经过推理、计算可求出线段CQ的长．请你任选其中一种方案求线段CQ的长．

【中考模拟练】

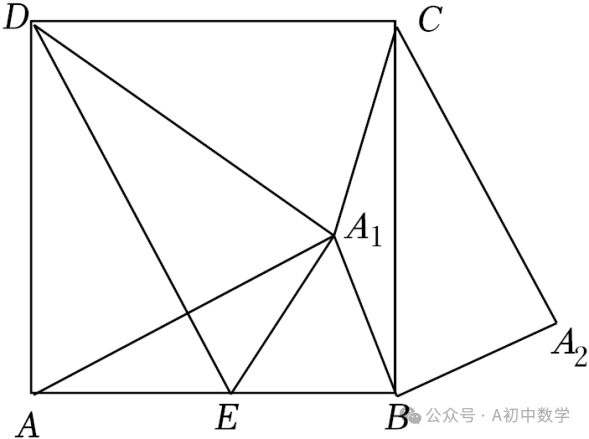
1．（2024•天山区校级一模）如图，正方形ABCD边长为1，点E在边AB上（不与A，B重合），将△ADE沿直线DE折叠，点A落在点A₁处，连接A₁B，将A₁B绕点B顺时针旋转90°得到A₂B，连接A₁A，A₁C，A₂C．给出下列四个结论：

①△ABA₁≌△CBA₂；

②∠ADE+∠A₁CB＝45°；

③点P是直线DE上动点，则CP+A₁P的最小值为；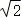

④当∠ADE＝30°时，△A₁BE的面积为．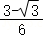

其中正确的结论个数是（　　）

A．1B．2C．3D．4

2．（2024•曲阜市一模）如图1，菱形纸片ABCD的边长为2，∠ABC＝60°，如图2，翻折∠ABC，∠ADC，使两个角的顶点重合于对角线BD上一点P，EF，GH分别是折痕．设AE＝x（0＜x＜2），给出下列判断：

①当x＝1时，DP的长为；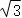

②EF+GH的值随x的变化而变化；

③六边形AEFCHG面积的最大值是；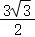

④六边形AEFCHG周长的值不变．

其中正确的是（　　）

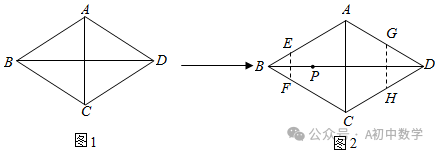
A．①②B．①④C．②③④   D．①③④

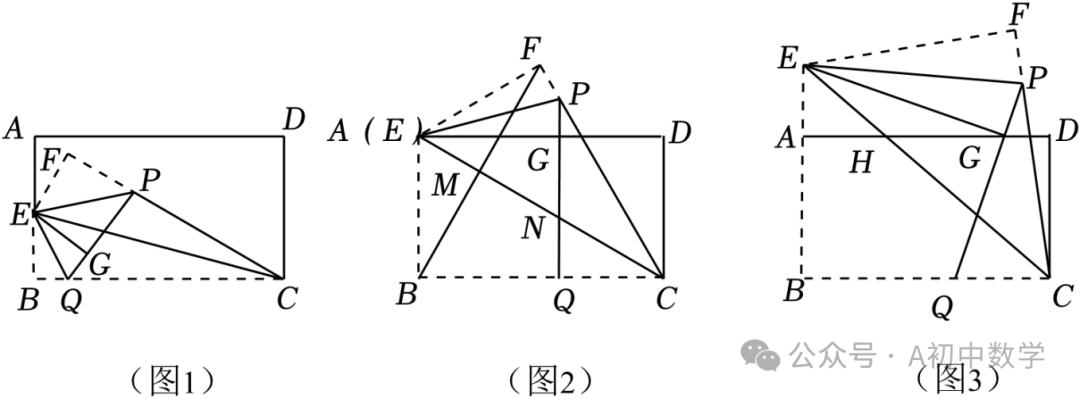
3．（2024•辽宁模拟）如图，在矩形ABCD中，AB＝2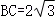，，点E为射线BA上一点（点E不与点B重合），将△BCE沿EC折叠，得到△FCE，点P为线段FC上一点，再将△EFP沿EP折叠，得到△EGP，PG的延长线与边BC相交于点Q．

（1）如图1，连接EQ，求证：QB＝QG．

（2）如图2，当点E与点A重合时，若点G落在边AD上，连接BF，EC与BF相交于点M，与PQ相交于点N，求MN的长．

（3）若点G落在边AD上，且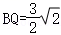，CE所在直线与AD所在直线相交于点H．

①如图3，当点E在线段BA延长线上时，求HG的长；

②当点E在线段AB上时，请直接写出HG的长．

题型二：四边形与旋转的综合

【中考真题练】

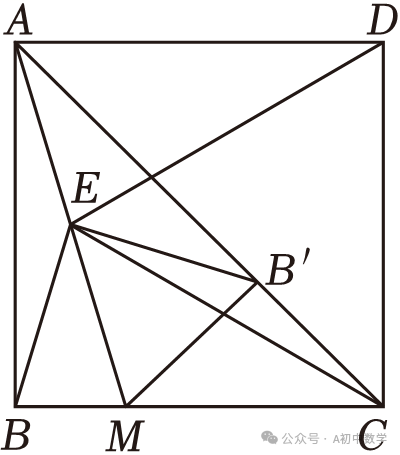
1．（2023•南充）如图，正方形ABCD中，点M在边BC上，点E是AM的中点，连接ED，EC．

（1）求证：ED＝EC；

（2）将BE绕点E逆时针旋转，使点B的对应点B′落在AC上，连接MB′．当点M在边BC上运动时（点M不与B，C重合），判断△CMB′的形状，并说明理由．

（3）在（2）的条件下，已知AB＝1，当∠DEB′＝45°时，求BM的长．

2．（2023•绍兴）在平行四边形ABCD中（顶点A，B，C，D按逆时针方向排列），AB＝12，AD＝10，∠B为锐角，且sinB＝．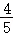

（1）如图1，求AB边上的高CH的长；

（2）P是边AB上的一动点，点C，D同时绕点P按逆时针方向旋转90°得点C'，D'，

①如图2，当C'落在射线CA上时，求BP的长；

②当△AC'D'是直角三角形时，求BP的长．

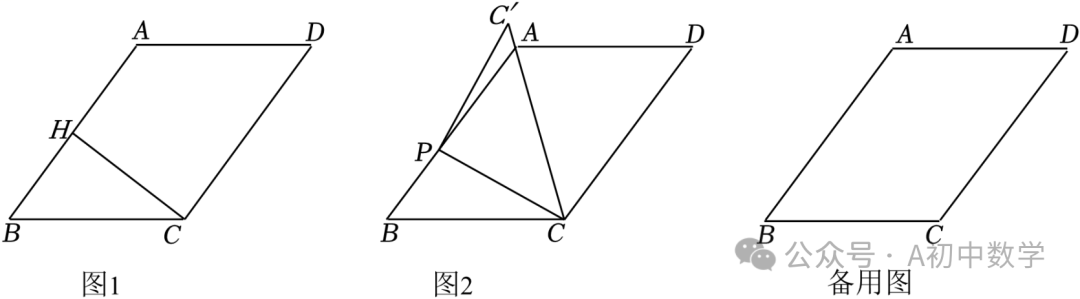
3．（2023•丹东）在△ABC中，∠BAC＝90°，∠ABC＝30°，AB＝6，点D是BC的中点．四边形DEFG是菱形（D，E，F，G按逆时针顺序排列），∠EDG＝60°，且DE＝2，菱形DEFG可以绕点D旋转，连接AG和CE，设直线AG和直线CE所夹的锐角为α．

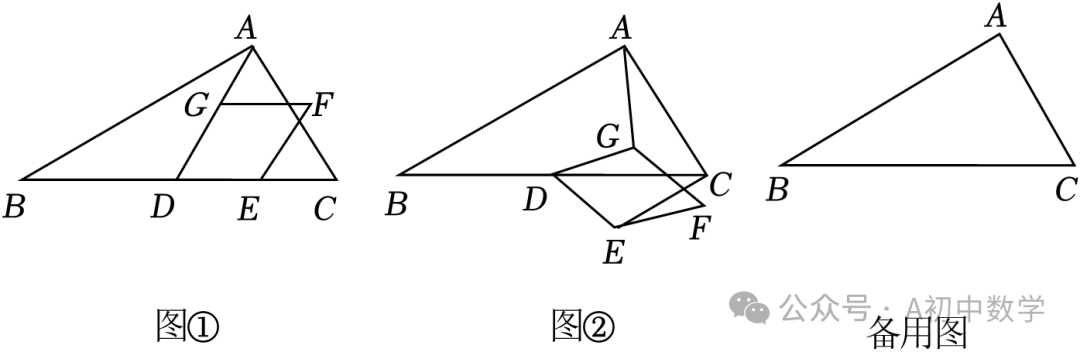
（1）在菱形DEFG绕点D旋转的过程中，当点E在线段DC上时，如图①，请直接写出AG与CE的数量关系及α的值；

（2）当菱形DEFG绕点D旋转到如图②所示的位置时，（1）中的结论是否成立？若成立，请写出证明过程；若不成立，请说明理由；

（3）设直线AG与直线CE的交点为P，在菱形DEFG绕点D旋转一周的过程中，当EF所在的直线经过点B时，请直接写出△APC的面积．

【中考模拟练】

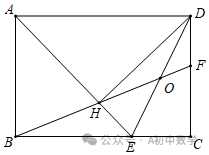
1．（2023•宁阳县一模）如图，Rt△ABE中，∠B＝90°，AB＝BE，将△ABE绕点A逆时针旋转45°，得到△AHD，过D作DC⊥BE交BE的延长线于点C，连接BH并延长交DC于点F，连接DE交BF于点O．下列结论：

①DE平分∠HDC；②DO＝OE；③H是BF的中点；④BC﹣CF＝2CE；

⑤CD＝HF，其中正确的有（　　）

A．5个B．4个C．3个D．2个

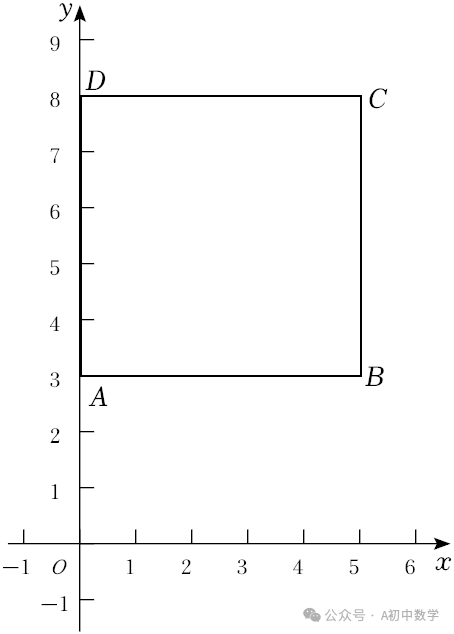
2．（2024•永修县一模）在平面直角坐标系中，正方形ABCD的边AD在y轴正半轴上，边BC在第一象限，且A（0，3）、B（5，3），将正方形ABCD绕点A顺时针旋转α（0°＜α＜180°），若点B的对应点B′恰好落在坐标轴上，则点C的对应点C′的坐标为                            ．

3．（2024•天津一模）在平面直角坐标系中，O为原点，△OAB是等腰直角三角形，∠OBA＝90°，点A（5，0），点B在第一象限，点P在边OA（点P不与点O，A重合），过点P作PQ⊥OA，交△OAB的直角边于点Q，将线段QP绕点Q逆时针旋转90°得到线段QM，点P的对应点为M，连接PM．

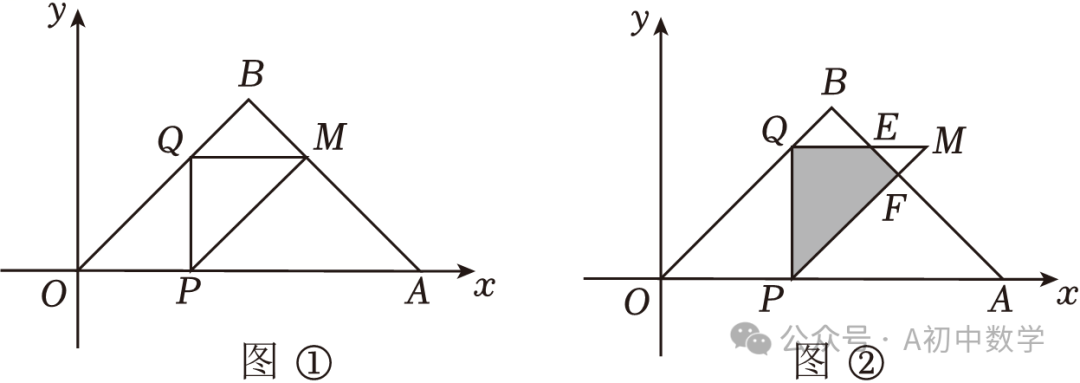
（1）如图①，若点M落在AB上，点B的坐标是        ，点M的坐标是          ；

（2）设△PQM与△OAB重合部分面积为S，OP＝t．

①如图②，若重合部分为四边形PQEF，与边AB交于点E，F，试用含t的式子表示S，并直接写出t的取值范围；

②当1≤t≤4时，求S的取值范围．（请直接写出结果即可）

题型三：四边形与新定义的综合

【中考真题练】

1．（2023•宁波）定义：有两个相邻的内角是直角，并且有两条邻边相等的四边形称为邻等四边形，相等两邻边的夹角称为邻等角．

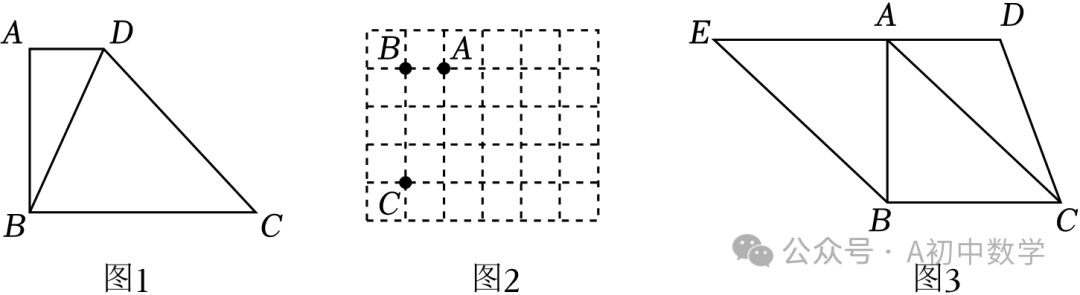
（1）如图1，在四边形ABCD中，AD∥BC，∠A＝90°，对角线BD平分∠ADC．求证：四边形ABCD为邻等四边形．

（2）如图2，在6×5的方格纸中，A，B，C三点均在格点上，若四边形ABCD是邻等四边形，请画出所有符合条件的格点D．

（3）如图3，四边形ABCD是邻等四边形，∠DAB＝∠ABC＝90°，∠BCD为邻等角，连结AC，过B作BE∥AC交DA的延长线于点E．若AC＝8，DE＝10，求四边形EBCD的周长．

2．（2023•常州）对于平面内的一个四边形，若存在点O，使得该四边形的一条对角线绕点O旋转一定角度后能与另一条对角线重合，则称该四边形为“可旋四边形”，点O是该四边形的一个“旋点”．例如，在矩形MNPQ中，对角线MP、NQ相交于点T，则点T是矩形MNPQ的一个“旋点”．

（1）若菱形ABCD为“可旋四边形”，其面积是4，则菱形ABCD的边长是    ；

（2）如图1，四边形ABCD为“可旋四边形”，边AB的中点O是四边形ABCD的一个“旋点”．求∠ACB的度数；

（3）如图2，在四边形ABCD中，AC＝BD，AD与BC不平行．四边形ABCD是否为“可旋四边形”？请说明理由．

3．（2023•淮安）综合与实践

定义：将宽与长的比值为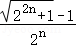（n为正整数）的矩形称为n阶奇妙矩形．

（1）概念理解：

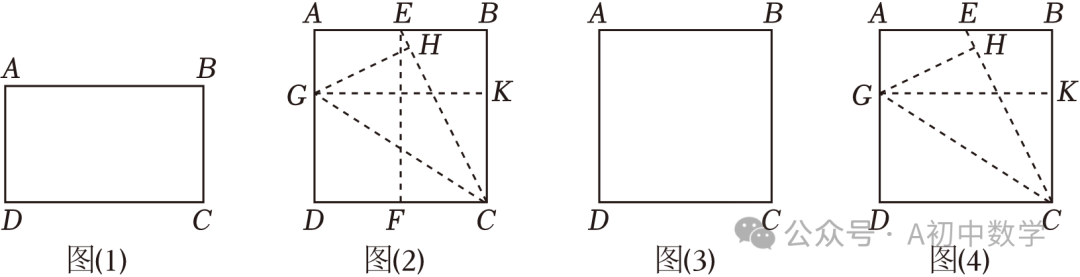
当n＝1时，这个矩形为1阶奇妙矩形，如图（1），这就是我们学习过的黄金矩形，它的宽（AD）与长（CD）的比值是 ．

（2）操作验证：

用正方形纸片ABCD进行如下操作（如图（2））：

第一步：对折正方形纸片，展开，折痕为EF，连接CE；

第二步：折叠纸片使CD落在CE上，点D的对应点为点H，展开，折痕为CG；

第三步：过点G折叠纸片，使得点A、B分别落在边AD、BC上，展开，折痕为GK．

试说明：矩形GDCK是1阶奇妙矩形．

（3）方法迁移：

用正方形纸片ABCD折叠出一个2阶奇妙矩形．要求：在图（3）中画出折叠示意图并作简要标注．

（4）探究发现：

小明操作发现任一个n阶奇妙矩形都可以通过折纸得到．他还发现：如图（4），点E为正方形ABCD边AB上（不与端点重合）任意一点，连接CE，继续（2）中操作的第二步、第三步，四边形AGHE的周长与矩形GDCK的周长比值总是定值．请写出这个定值，并说明理由．

【中考模拟练】

1．（2024•泰兴市一模）【定义呈现】有两个内角分别是它们对角的两倍的四边形叫做倍对角四边形．其中，这两个内角称为倍角．例如：如图1，在四边形ABCD中，∠A＝2∠C，∠D＝2∠B，那么我们就叫这个四边形是倍对角四边形，其中∠A，∠D称为倍角．

【定义理解】如图1，四边形ABCD是倍对角四边形，且∠A，∠D是倍角．求∠B+∠C的度数；

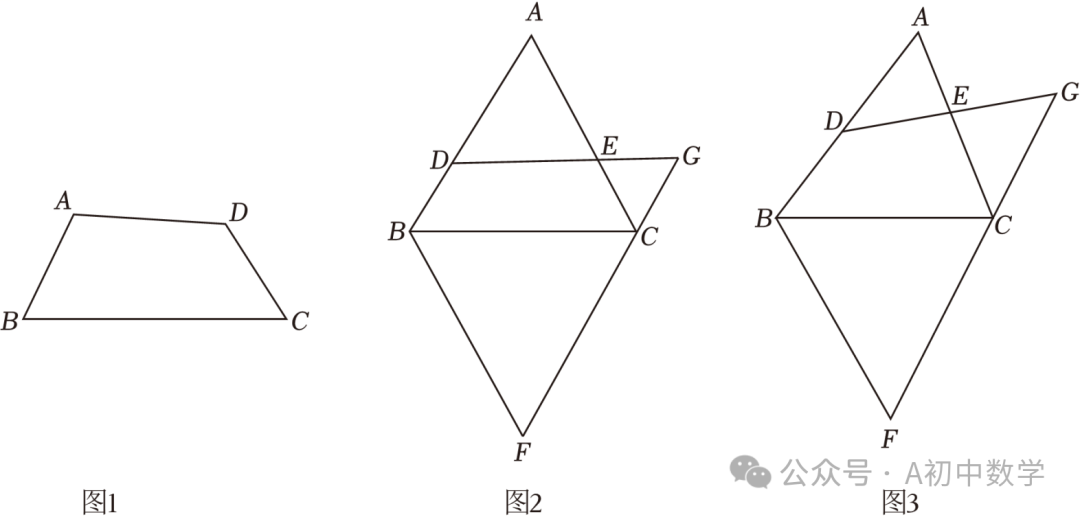
【拓展提升】如图2，四边形BDEC是倍对角四边形，且∠DEC，∠BDE是倍角，延长BD、CE交于点A．在BC下方作等边△BCF，延长FC、DE交于点G．若AB＝AC，BC＝2，FG＝kAB，四边形BDEC的周长记为l．

（1）用k的代数式表示l；

（2）如图3，把题中的“AB＝AC”条件舍去，其它条件不变．

①求证：CE＝EG；

②探究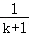是否为定值．如果是定值，求这个定值，如果不是，请说明理由．

题型四：四边形与中点的综合

【中考真题练】

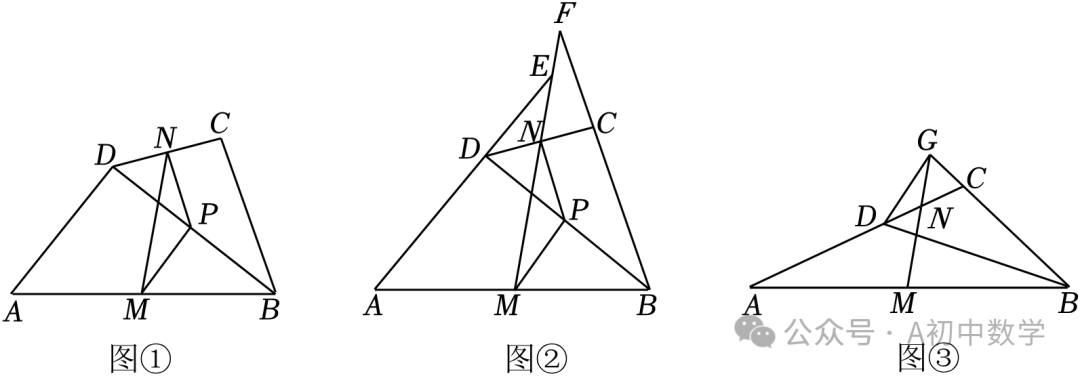
1．（2023•镇江）[发现]如图1，有一张三角形纸片ABC，小宏做如下操作：

①取AB、AC的中点D、E，在边BC上作MN＝DE．

②连接EM，过点D、N作DG⊥EM、NH⊥EM，垂足分别为G、H．

③将四边形BDGM剪下，绕点D旋转180°至四边形ADPQ的位置，将四边形CEHN剪下，绕点E旋转180°至四边形AEST的位置．

④延长PQ、ST交于点F．

小宏发现并证明了以下几个结论是正确的：

①点Q、A、T在一条直线上；

②四边形FPGS是矩形；

③△FQT≌△HMN；

④四边形FPGS与△ABC的面积相等．

[任务1]请你对结论①进行证明．

[任务2]如图2，四边形ABCD中，AD∥BC，P、Q分别是AB、CD的中点，连接PQ．求证：PQ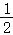＝（AD+BC）．

[任务3]如图3，有一张四边形纸片ABCD，AD∥BC，AD＝2，BC＝8，CD＝9，sin∠DCB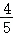＝，小丽分别取AB、CD的中点P、Q，在边BC上作MN＝PQ，连接MQ，她仿照小宏的操作，将四边形ABCD分割、拼成了矩形．如果她拼成的矩形恰好是正方形，求BM的长．

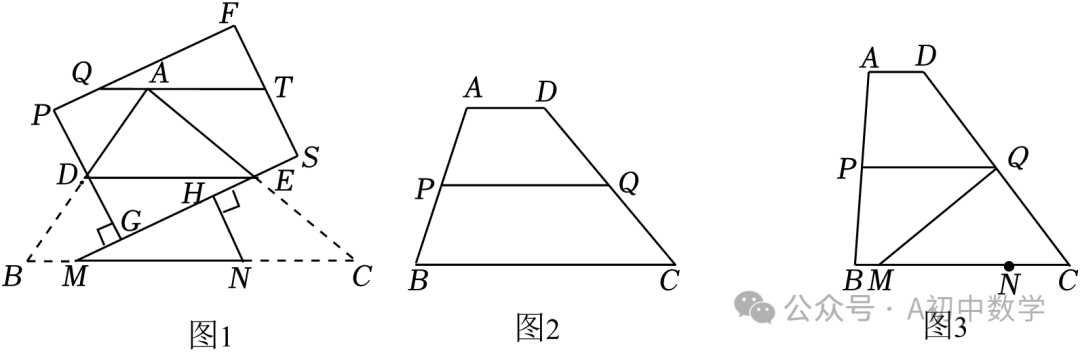
2．（2023•东营）（1）用数学的眼光观察

如图①，在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是AB的中点，N是DC的中点．求证：∠PMN＝∠PNM．

（2）用数学的思维思考

如图②，延长图①中的线段AD交MN的延长线于点E，延长线段BC交MN的延长线于点F．求证：∠AEM＝∠F．

（3）用数学的语言表达

如图③，在△ABC中，AC＜AB，点D在AC上，AD＝BC，M是AB的中点，N是DC的中点，连接MN并延长，与BC的延长线交于点G，连接GD．若∠ANM＝60°，试判断△CGD的形状，并进行证明．

【中考模拟练】

1．（2024•泗阳县校级二模）综合与实践

探究几何元素之间的关系

问题情境：四边形ABCD中，点O是对角线AC的中点，点E是直线AC上的一个动点（点E与点C，O，A都不重合），过点A，C分别作直线BE的垂线，垂足分别为F，G，连接OF，OG．

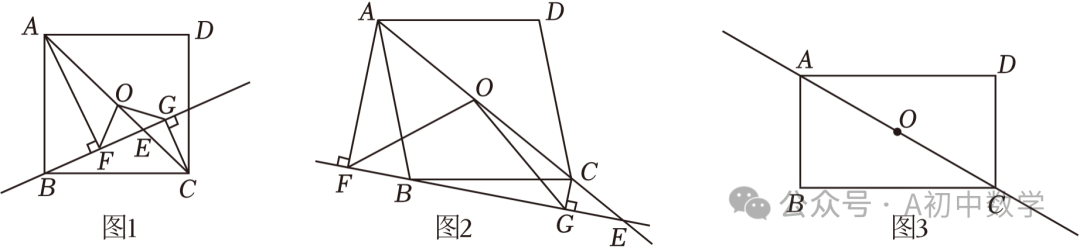
（1）初步探究：

如图1，已知四边形ABCD是正方形，且点E在线段OC上，求证AF＝BG；

（2）深入思考：请从下面A，B两题中任选一题作答，我选择           题．

A．探究图1中OF与OG的数量关系并说明理由；

B．如图2，已知四边形ABCD为菱形，且点E在AC的延长线上，其余条件不变，探究OF与OG的数量关系并说明理由；

（3）拓展延伸：请从下面AB两题中任选一题作答，我选择       题．

如图3，已知四边形ABCD为矩形，且AB＝4，∠BAC＝60°．

A．点E在直线AC上运动的过程中，若BF＝BG，则FG的长为   ．

B．点E在直线AC上运动的过程中，若OF//BC，则FG的长为                      ．

 由于篇幅有限，答案较长，需要参考答案的朋友们请在文末获取哦！