中考数学 | 图形几何变换【一次函数综合题】解答题专练(有答案)
四季读书网
40
初中数学知识和小学阶段相比,逐渐显现出了数学的抽象特点。但是同学们别担心,让我们跟随王老师的脚步,一起来看看数学究竟是怎么一回事吧!相信同学们会发现,数学原来并不难,数学还挺有趣的。今天和大家分享的是中考数学 | 图形几何变换【一次函数综合题】解答题专练(有答案)!
中考数学 | 图形几何变换
【一次函数综合题】解答题
【一】如图,在平面直角坐标系xOy中,直线l:y=-4/3x+4与x轴、y轴分别相交于B、A两点,点C是AB的中点,点E、F分别为线段AB、OB上的动点,将△BEF沿EF折叠,使点B的对称点D恰好落在线段OA上(不与端点重合).连接OC分别交DE、DF于点M、N,连接FM.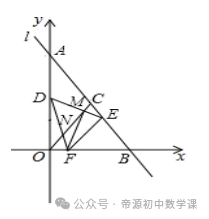
则∠COB=∠CBO=∠EDF=α,∠ONF=∠DNM,则tan∠NFO=NH/NF=24/7=tanβ,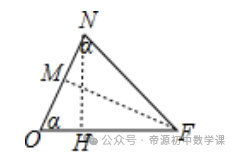
sin∠NFO=HN/NF=24/25=sinβ,则cosβ=7/25cos∠DFO=cosβ=m/3﹣m,解得:m=21/3,OD2=DF2﹣OF2=(3﹣m)2﹣m2=81/16;则OD=9/4,【二】如图,直线y=﹣2x+7与x轴、y轴分别相交于点C、B,与直线y=3/2x相交于点A.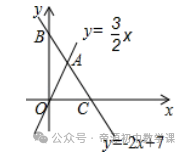
(2)如果在y轴上存在一点P,使△OAP是以OA为底边的等腰三角形,则P点坐标是(0,13/6);∴OP=PA,∴22+(3﹣y)2=y2,解得y=13/6,(3)在直线y=﹣2x+7上是否存在点Q,使△OAQ的面积等于6?若存在,请求出Q点的坐标,若不存在,请说明理由.由直线y=﹣2x+7可知B(0,7),C(7/2,0),∴Q点有两个位置:Q在线段AB上和AC的延长线上,设点Q的坐标是(x,y),当Q点在线段AB上:作QD⊥y轴于点D,如图①,则QD=x,∴S△OBQ=S△OAB﹣S△OAQ=7﹣6=1,∴1/2OB•QD=1,即1/2×7x=1,∴x=2/7,当Q点在AC的延长线上时,作QD⊥x轴于点D,如图②则QD=﹣y,∴S△OCQ=S△OAQ﹣S△OAC=6-21/4=3/4∴1/2OC•QD=3/4,即1/2×7/2×(﹣y)=3/4,把y=-3/7代入y=﹣2x+7,解得x=26/7,综上所述:点Q是坐标是(2/7,45/7)或(26/7,-3/7).【三】对于平面直角坐标系xOy中的点A和点P,若将点P绕点A逆时针旋转90°后得到点Q,则称点Q为点P关于点A的“垂链点”,图1为点P关于点A的“垂链点”Q的示意图.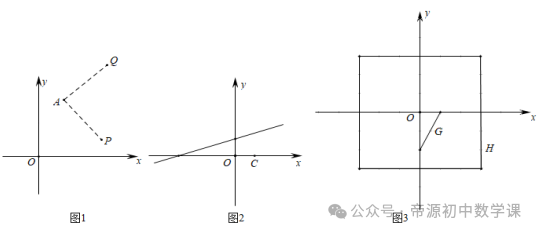
(1)已知点A的坐标为(0,0),点P关于点A的“垂链点”为点Q;①若点P的坐标为(2,0),则点Q的坐标为 (0,2) .②若点Q的坐标为(﹣2,1),则点P的坐标为 (1,2) .根据旋转的性质得:①点Q(0,2),点P(1,2),(2)如图2,已知点C的坐标为(1,0),点D在直线y=1/3x+1上,若点D关于点C的“垂链点”在坐标轴上,试求出点D的坐标.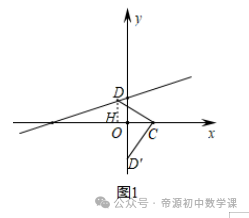
则点D关于点C的“垂链点”在x轴上,点CD⊥x轴,∵∠DCH+∠HDC=90°,∠OCD′+∠DCH=90°,则DH=OC,即:1/3m+1=1,解得:m=0,(3)如图3,已知图形G是端点为(1,0)和(0,﹣2)的线段,图形H是以点O为中心,各边分别与坐标轴平行的边长为6的正方形,点M为图形G上的动点,点N为图形H上的动点,若存在点T(0,t),使得点M关于点T的“垂链点”恰为点N,请直接写出t的取值范围.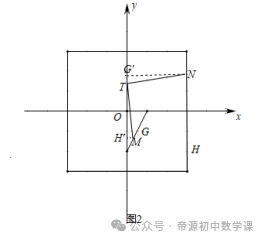
当﹣3时,点M关于点T的“垂链点”恰为点N在正方形的边上,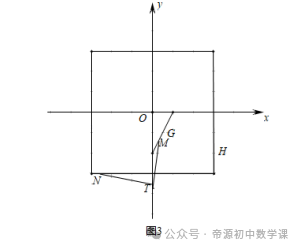
综上,t的取值范围为:1≤t<7/3或-11/3<t≤﹣3.【四】如图1,已知函数y=1/2x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.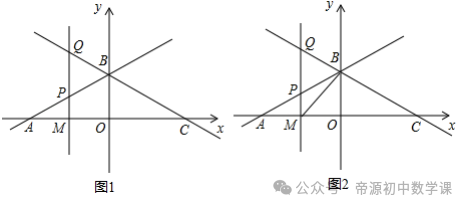
由y=0得:y=1/2x+3,解得x=﹣6,∴A(﹣6,0),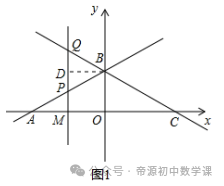
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.则P(m,1/2m+3)、Q(m,-1/2m+3)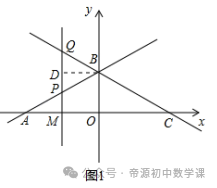
∴S△PQB=1/2PQ•BD=1/2m2=8/3,②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.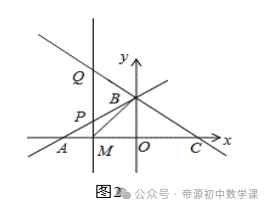
∴∠MBC=180°﹣(∠BMC+∠BCA)=90°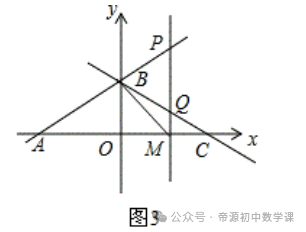
综上,点P的坐标为(-3/2,9/4)或(3/2,15/4).
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!





















