👇👇👇免费进学习群!
以微课堂学习群
奥数国家级教练与四名特级
教师联手执教。
这讲重点讲解通过构造直角三角形斜边上的中线结合中位线来解决问题
I先来关注一类重要题型:共斜边的两个直角三角形
例1 已知:在RT△ABC和RT△ADC中,∠ABC=∠ADC=90°,E、F分别为AC和BD的中点,
(1)求证:EF⊥BD;
(2)若∠BAD=45°求AC:EF的值.
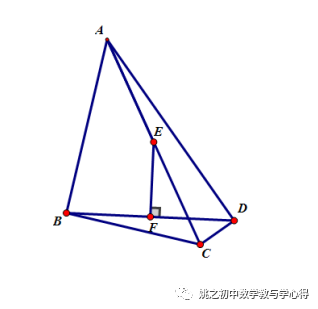
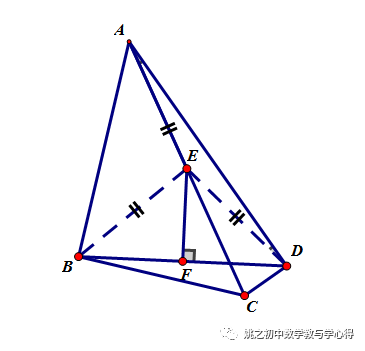
简析:(1)E为两个直角三角形斜边中点,连BE、DE ,得:BE=AE=DE,又F为BD中点,三线合一得EF⊥BD
(2)导角:∠ABE=∠BAE,∠DAE=∠ADE,由外角性质可证∠BED=2∠BAD=90°,△BED为等腰直角三角形,设EF=1,则BE=√2,AC=2√2,AC:EF=2√2
配套练习:
1、已知:四边形ABCD中,∠ABC=∠ADC=90°,∠BCD=120°,连接AC、BD,求AC:BD的值.
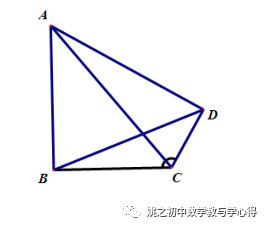
(解法参考例1第二步)
练习2 已知锐角△ABC中,两条高AD、CE相交于点F,连BF,G、H分别为BF、AC中点,连接DE、GH
求证:GH垂直平分DE.
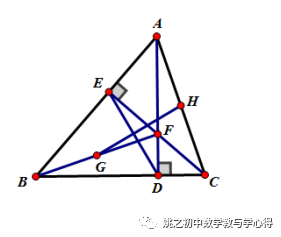
(提示:连EG、DG、EH、DH)
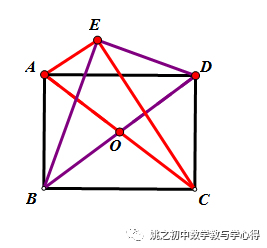
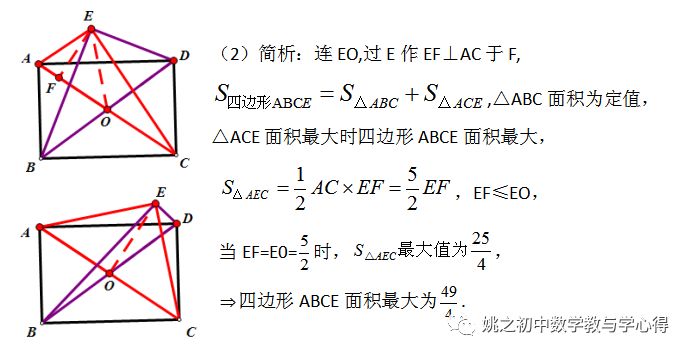
例2 已知:□ABCD中,AB=3,BC=4,E为□ABCD外一点,∠AEC=∠BED=90°,
(1)求□ABCD的面积;
(2)求四边形ABCE面积的最大值.

参考例2(2)来道相关的面积最值题练习,孩子们自己完成吧:
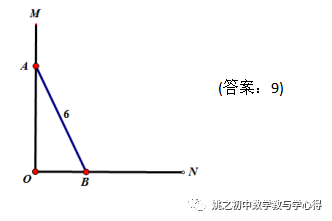
已知:∠MON=90°,线段AB=6,两端点A、B分别在OM、ON上运动,求△AOB面积的最大值.
II结合直角三角形斜边上中线和中位线解决与角有关的问题:
例3 已知:AD、AE分别是△ABC的高和中线
(1)若DE=0.5AC ,求证:∠B=0.5∠C
(2)若∠B=0.5∠C, 求证:DE=0.5AC
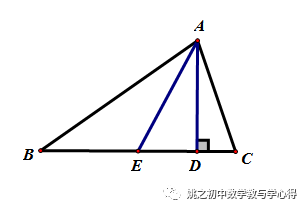
简析:取AB中点F,连DF、EF,
(1)易证DE=0.5AC=EF,∠1=∠2=0.5∠3,又∠1=∠B,∠3=∠C,
得∠B=0.5∠C
(2)与(1)反其道而证之!
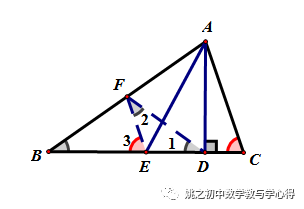
练习3 已知:△ABC中,AD是高,E、F、G分别是BC、BA、AC边上的点,连DF、DG、EF、EG
求证:∠FEG=∠FDG.
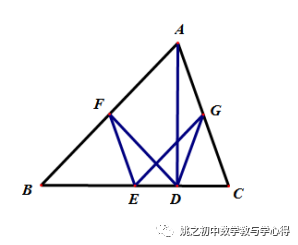
练习4 已知菱形ABCD中,对角线AC、BD交于点O,DE⊥AB于点O,连OE,
求证:∠DEO=∠DAO.
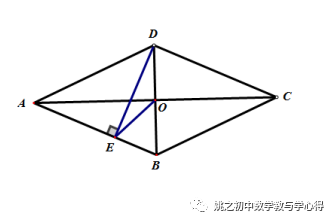

例4 已知:RT△ADB和RT△AEC中,∠ADB=∠AEC=90°,∠DAB=∠EAC,连BC,取中点O,连DO、CO,
求证:DO=CO.
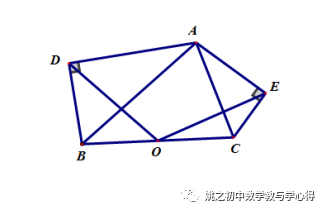

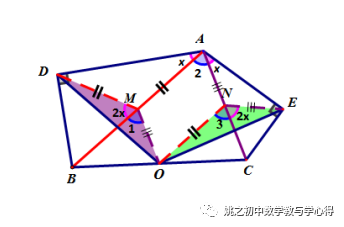
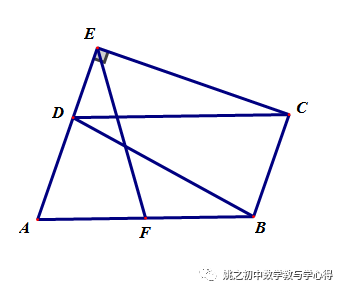
练习6 已知△ABC中,D为BC中点,E、F分别在AB、AC延长线上,且DE=DF,分别过E、F作AB、AC的垂线,两垂线相交于点G,
求证:∠EGB=∠FGC.
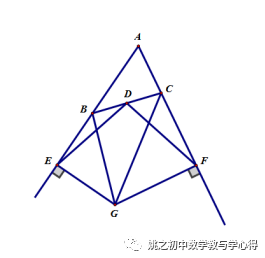
提示:辅助线如下图,思路参考例4
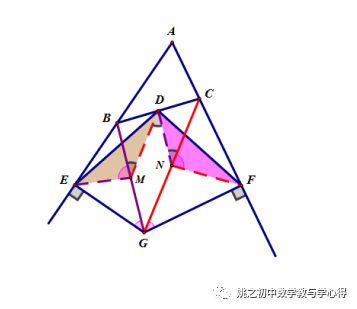
小结:题中有直角三角形,可尝试作直角三角形斜边上中线,再根据其性质,来分析、解决问题。
👇👇👇免费进学习群!
以微课堂学习群
奥数国家级教练与四名特级
教师联手执教。






