中考数学冲刺复习之二次函数-定点、定值问题

中考数学冲刺复习之二次函数－定点、定值问题

中考数学冲刺复习

二次函数

定点、定值问题

题型一 面积（面积比）定值

题型二 线段（线段比）定值

题型三 线段和差倍定值师型，段乘积本

数学陈老师:

【题型一 面积（面积比）定值】

1.已知，抛物线y=x²-(2m+2)x+㎡+2m与x轴交于A,B两点（A在B的左侧）．

（1)当m=0时，求点A,B坐标；

（2)若直线y=-x+b经过点A,且与抛物线交于另一点C,连接AC,BC,试判断ΔABC的面积是否发生变化？若不变，请求出ΔABC的面积；若发生变化，请说明理由；

（3)当5-2m≤x≤2m-1时，若抛物线在该范围内的最高点为M,最低点为N,直线MN与x轴交于点D,且MD/ND＝3,求此时抛物线的解析式．    

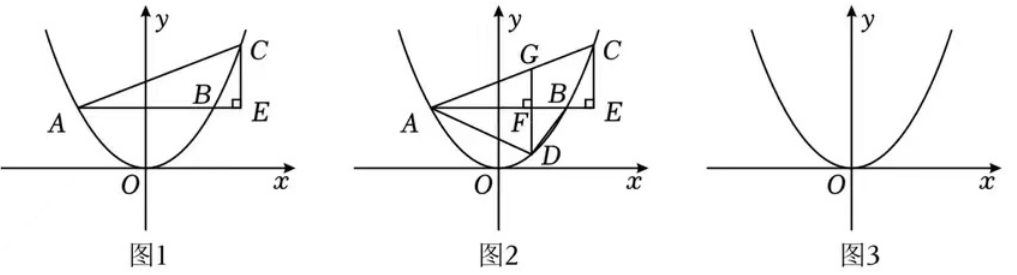
2.已知抛物线y=ax²(a＞0)经过第二象限的点A,过点A作AB//x轴交抛物线于点B,第一象限的点C为直线AB上方抛物线上的一个动点．过点C作CE⊥AB于E,连接AC、BC.

（1)如图1,若点A(-1, 1),CE=1.

    ①求a的值；

     ②求证：ΔACE∽ΔCBE.

（2)如图2,点D在线段AB下方的抛物线上运动（不与A、B重合），过点D作AB的垂线，分别交AB、AC于点F、G,连接AD、BD.若∠ADB=90°,求DF的值（用含有a的代数式表示）。

（3)在（2)的条件下，连接BG、DE,试判断S_△BGE/S_△DBE的值是否随点D的变化而变化？如果不变，求出S_△BGE/S_△DBE的值，如果变化，请说明理由。

数学陈老师:

【题型二 线段（线段比）定值】    

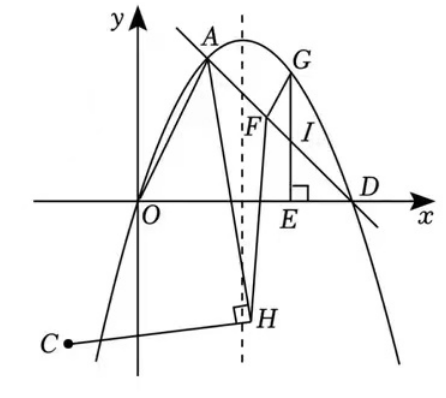
3.如图，抛物线经过ΔAOD的三个顶点，其中O为原点，A(2, 4),D(6, 0),点F在线段AD上运动，点G在直线AD上方的抛物线上，GF∥AO,GE⊥DO于点E,交AD于点I,AH平分∠OAD,C(-2,-4),AH⊥CH于点H,连接FH.

（1)求抛物线的解析式及ΔAOD的面积；

（2)当点F运动至抛物线的对称轴上时，求ΔAFH的面积；

（3)试探究GI/GI的值是否为定值？如果为定值，求出该定值；不为定值，请说明理由。

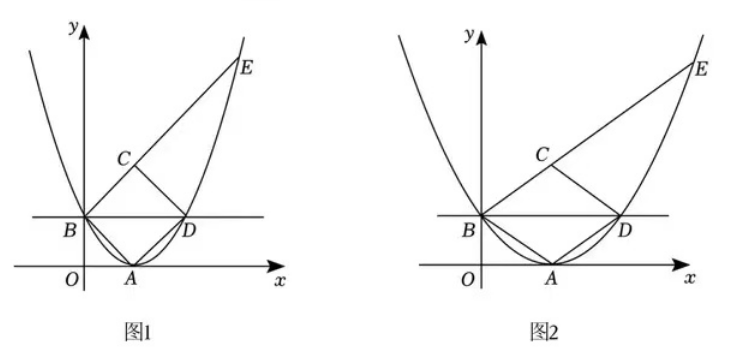
4.如图，一次函数y=--b/ax+b(a＞0,b＞0)与坐标轴交于A,B两点，以A为顶点的抛物线过点B,过点B作y轴的垂线交该抛物线于另一点D,以AB,AD为边构造平行四边形ABCD,延长BC交抛物线于点E.    

（1)若a=b=2,如图1.

    ①求该抛物线的表达式。

    ②求点E的坐标。

（2)如图2,请问BE/AB是否为定值，若是，请求出该定值；若不是，请说明理由。

数学陈老师:

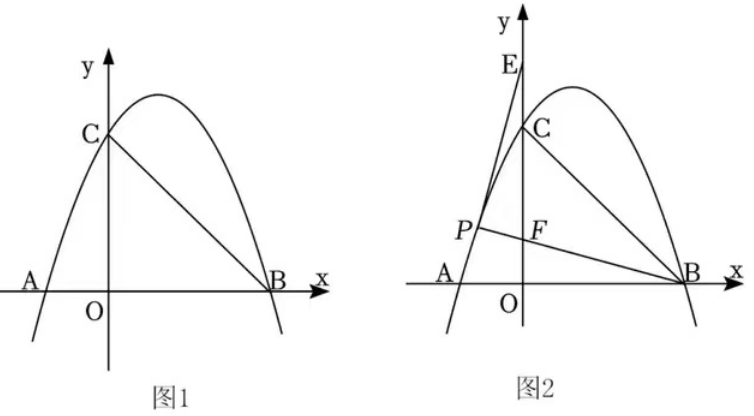
5.已知，抛物线y=ax²+bx+c经过A(-1, 0)、B(3, 0)、C(0, 3)三点，点P是抛物线上一点．

（1)求抛物线的解析式；

（2)当点P位于第四象限时，连接AC,BC,PC,若∠PCB=∠ACO,求直线PC的解析式；

（3)如图2,当点P位于第二象限时，过P点作直线AP,BP分别交y轴于E,F两点，请问CE/CF的值是否为定值？若是，请求出此定值；若不是，请说明理由。    

【题型三 线段和差倍定值】

6.已知抛物线y=ax²+bx+2(a,b为常数，a≠0)经过点A(-1, 0),B(3, 0),与y轴相交于点C,其对称轴与x轴相交于点E.

（1)求该抛物线的解析式；

（2)连接BC,在该抛物线上是否存在点P,使∠PCB=∠ABC?若存在，请求出点P的坐标；若不存在，请说明理由；

（3)Q为x轴上方抛物线上的动点，过点Q作直线AQ,BQ,分别交抛物线的对称轴于点M,N,点Q在运动过程中，EM+EN的值是否为定值？若是，请求出该定值；若不是，请说明理由。

数学陈老师:    

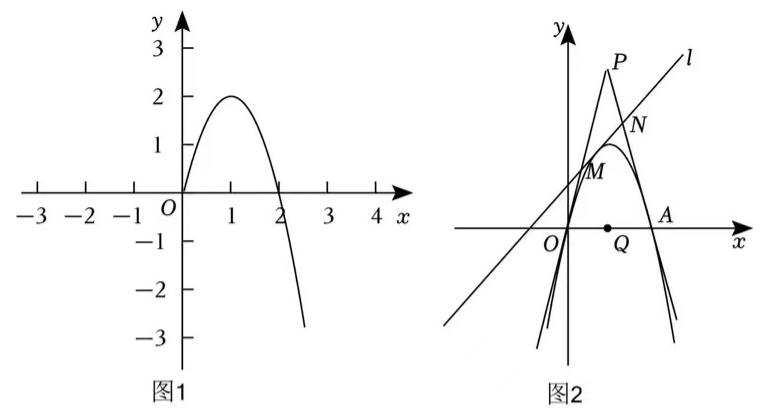
7.探究函数y=-2|x|²+4|x|的图象和性质，探究过程如下：

（1)自变量x的取值范围是全体实数，x与y的几组对应值列表如下：

其中，m=      .根据如表数据，在图1所示的平面直角坐标系中，通过描点画出了函数图象的一部分，请画出该函数图象的另一部分。观察图象，写出该函数的一条性质；

（2)点F是函数y=-2|x|²+4|x|图象上的一动点，点A(2, 0),点B(-2, 0),当S_△FAB=3时，请直接写出所有满足条件的点F的坐标；

（3)在图2中，当x在一切实数范围内时，抛物线y=-2x²+4x交x轴于O,A两点（点O在点A的左边），点P是点Q(1, 0)关于抛物线顶点的对称点，不平行y轴的直线l分别交线段OP,AP(不含端点）于M,N两点。当直线l与抛物线只有一个公共点时，PM与PN的和是否为定值？若是，求出此定值；若不是，请说明理由。    

数学陈老师:

8.综合与探究．

如图1,在平面直角坐标系中，已知二次函数y=-2/3x²+4/3x+2的图象与x轴交于A,B两点（点A在点B的左侧），与y轴交于点C,连接BC.

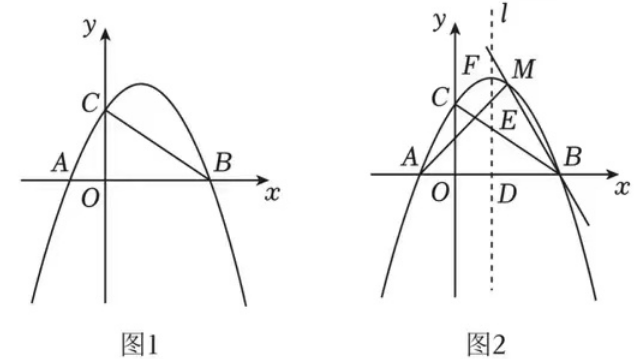
（1)求A,B,C三点的坐标，并直接写出直线BC的函数表达式；    

（2)点P是二次函数图象上的一个动点，请问是否存在点P使∠PCB=∠ABC?若存在，请求出点P的坐标；若不存在，请说明理由；

（3)如图2,作出该二次函数图象的对称轴直线l,交x轴于点D.若点M是二次函数图象上一动点，且点M始终位于x轴上方，作直线AM,BM,分别交l于点E,F,在点M的运动过程中，DE+DF的值是否为定值？若是，请直接写出该定值；若不是，请说明理由。

数学陈老师:

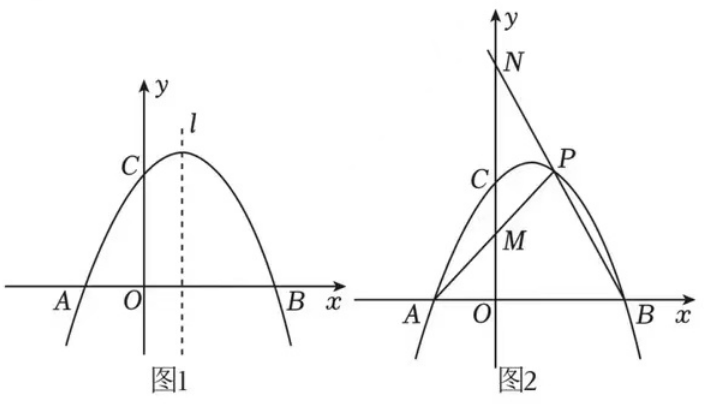
9.如图1,在平面直角坐标系中，已知二次函数y=ax²+bx+4的图象与x轴交于点A(-2, 0),B(4, 0),与y轴交于点C.

（1)求抛物线的解析式；

（2)已知E为抛物线上一点，F为抛物线对称轴l上一点，以B,E,F为顶点的三角形是等腰直角三角形，且∠BFE=90°,求出点F的坐标；

（3)如图2,P为第一象限内抛物线上一点，连接AP交y轴于点M,连接BP并延长交y轴于点N,在点P运动过程中，OM+1/2ON是否为定值？若是，求出这个定值；若不是，请说明理由。    

数学陈老师:

10.在平面直角坐标系xOy中，已知点A在y轴正半轴上．

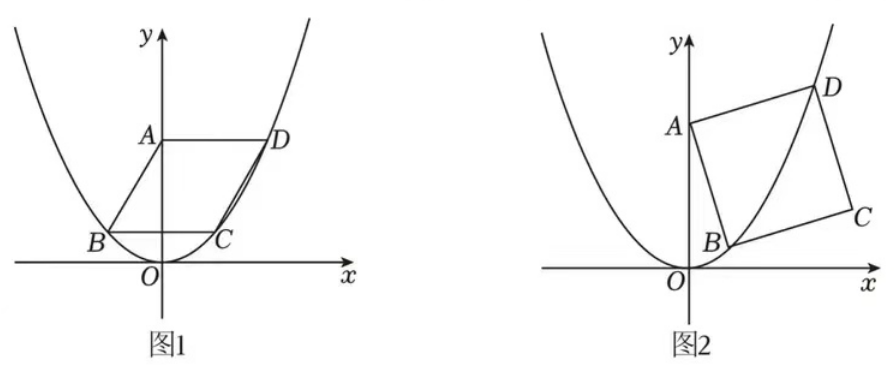
（1)如果四个点（0, 0)、（0, 2)、（1, 1)、（－1, 1)中恰有三个点在二次函数y=ax²(a为常数，且a≠0)的图象上．

    ①a=      ;

    ②如图1,已知菱形ABCD的顶点B、C、D在该二次函数的图象上，且AD⊥y轴，求菱形的边长；

    ③如图2,已知正方形ABCD的顶点B、D在该二次函数的图象上，点B、D在y轴的同侧，且点B在点D的左侧，设点B、D的横坐标分别为m、n,试探究n-m是否为定值。如果是，求出这个值；如果不是，请说明理由。

（2)已知正方形ABCD的顶点B、D在二次函数y=ax²(a为常数，且a＞0)的图象上，点B在点D的左侧，设点B、D的横坐标分别为m、n,直接写出m、n满足的等量关系式。    

点赞+关注

天天学习不迷路

赞赏后请留言

可提供答案解析

空白电子文档