2024成都青羊区中考二诊数学填空压轴,线段比最大值,5种方法解决!

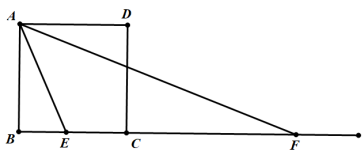
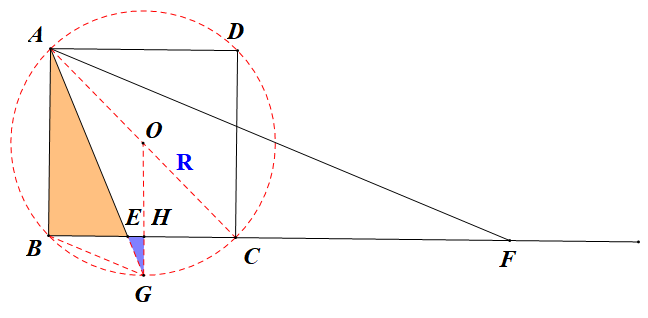
(2024成都市青羊区二诊)如图，在正方形ABCD，点E，F在射线BC上，∠EAF＝45°，则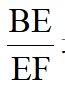最大值是 　   　．

解：方法一：引入外接圆

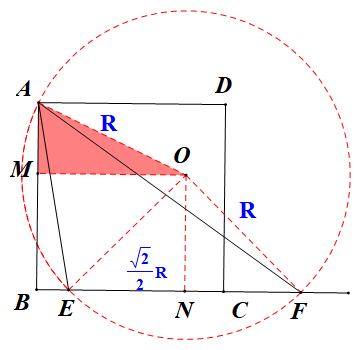
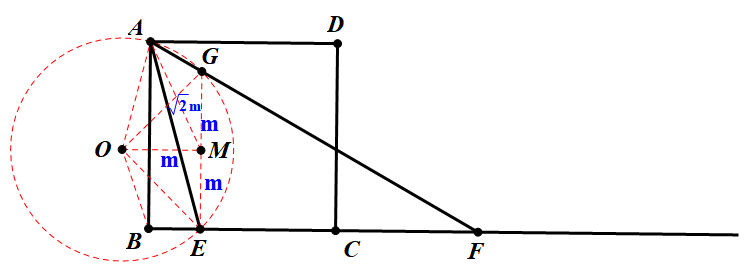
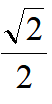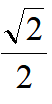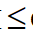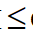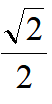由∠EAF=45°，联想到引入过点△AEF的外接圆，圆心为O，连接OA、OE、OF，作OM⊥AB，ON⊥BC，设半径OA=R，EF=R则EN=R，BE=OM-EN=OM-R，而OMOA，得NER-R，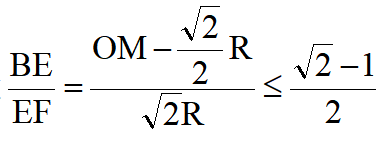

方法二：二次相似转化

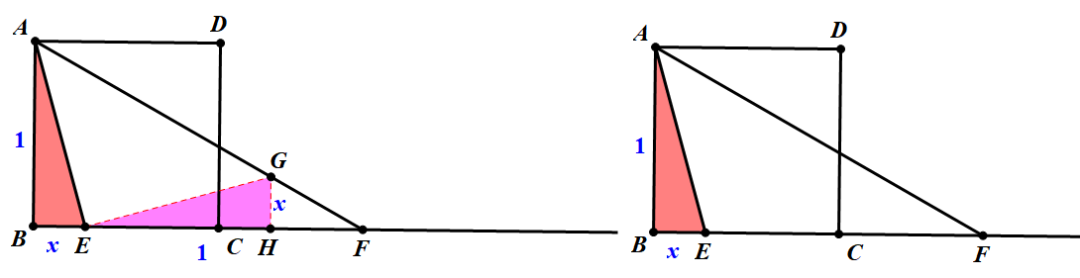
设AB=1，过点B作BG||AF，可得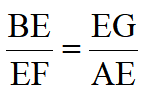，作GH⊥BF，得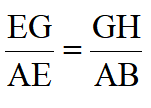，当GH取最大值时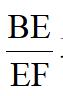，取最大值，易知点A、B、G、C共圆，当O、H、G共线时，GH取最大值，GHmax=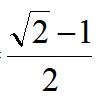故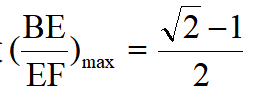

方法三：

设AB=1，过点E作EG||AF交AB于点G，则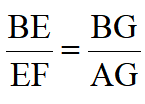得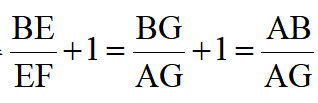，当AG取最小值时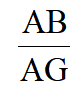，取最大值，易知AM=OM=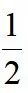m，OA=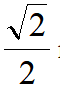m,OM+OEMN,当E、N重合时取等号，此时，

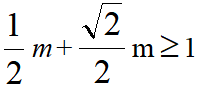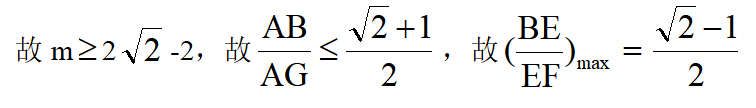
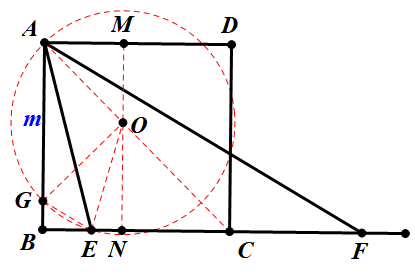
方法四：设AB=1，过点E作EG||AB交AF于点G，取过点A、G、E的外接圆，圆心为O，EG的中点M，设OM=m，则MG=ME=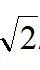m，则AM=，AM+ME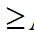AB,即有，，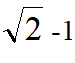

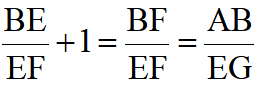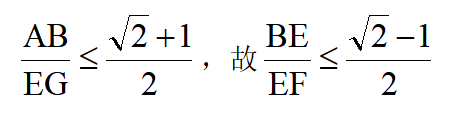
方法五：判别式法

3.出可利用相似求EF的长.

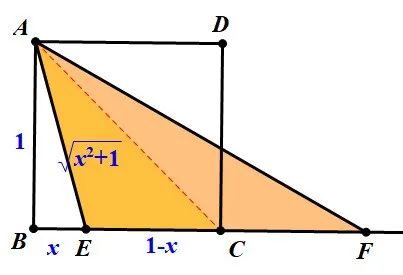
点评：BE、EF都是变化的，核心方法是转化，而转化的方法则有相似、共圆，找不等关系.

经过了不断的积累和沉淀，不断对中考数学题型的研究与总结，《中考压轴专题》隆重推出，帮助同学们提升实力.本书包含6个大专题，每个专题下包含多个考点和题型，力求覆盖所有压轴题型.题目取自中考真题、平时模拟真题中的压轴题、经典题，可帮助同学们精准训练，提升解题能力.

关于学霸数学

＂学霸数学＂专注于数学中考高考考试的最新信息，好题与压轴题解题技巧、知识专题分析以及考试分析与解答，考试动向及政策分析解读、家庭教育相关分享！如果您是家长或学生，对学习方面有任何问题，请联系小编！