中考数学冲刺复习之动点最值问题（费马点模型）
中考数学冲刺复习
动点最值问题
（费马点模型）
【费马点模型】
如图，在ΔABC内部找到一点P,使得PA+PB+PC的值最小。
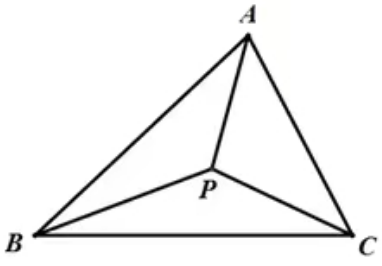
当点P满足∠APB=∠BPC=∠CPA=120°,
则PA+PB+PC的值最小，P点称为三角形的费马点．
特别地，ΔABC中，最大的角要小于120°,若最大的角大于或等于120°,此时费马点就是最大角的顶点A.（这种情况一般不考，通常三角形的最大顶角都小于120°)
【费马点的性质】
1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°.
【费马点最小值解法】
以ΔABC任意一边为边向外作等边三角形，
这条边所对两顶点的距离即为最小值.
证明过程：
将ΔAPC边以A为顶点逆时针旋转60°,得到AQE,连接PQ,则ΔAPQ为等边三角形，PA=PQ.
即PA+PB+PC=PQ+PB+PC,当B、P、Q、E四点共线时取得最小值BE.
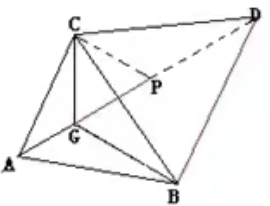
例题1.已知：ΔABC是锐角三角形，G是三角形内一点。
∠AGC=∠AGB=∠BGC=120°.
求证：GA+GB+GC的值最小。
数学陈老师:
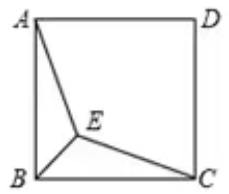
例题2.已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为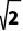
+
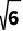,求正方形的边长．
【变式训练1】
已知点P是ΔABC内一点，且它到三角形的三个顶点距离之和最小，则P点叫ΔABC的费马点。已经证明：在三个内角均小于120°的ΔABC中，当∠APB=∠APC=∠BPC=120°时，P就是ΔABC的费马点。若点P是腰长为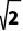的等腰直角三角形DEF的费马点，则PD+PE+PF= .
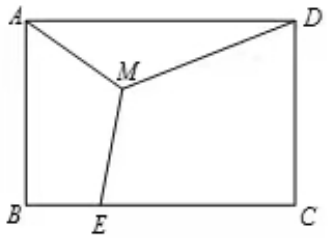
【变式训练2】
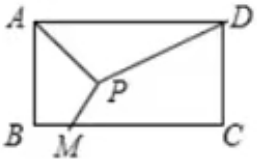
如图，已知矩形ABCD,AB=4,BC=6,点M为矩形内一点，点E为BC边上任意一点，则MA+MD+ME的最小值为 .
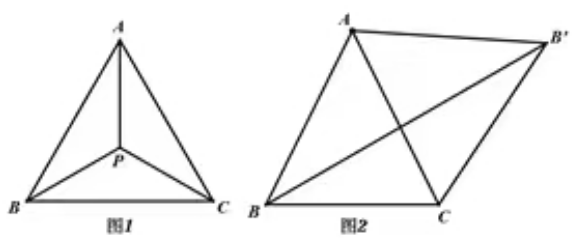
【变式训练3】
如图，P是锐角ΔABC所在平面上一点，如果∠APB=∠BPC=∠CPA=120°,则点P就叫做ΔABC费马点。
（1)当ΔABC是边长为4的等边三角形时，费马点P到BC边的距离为 ；
（2)若点P是ΔABC的费马点，∠ABC=60°,PA=2,PC=3,则PB的值为 ；
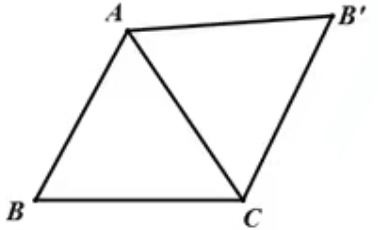
（3)如图2,在锐角ΔABC外侧作等边ΔACB',连接BB',求证：BB'过ΔABC的费马点P.
数学陈老师:
【变式训练4】
如图，某货运场为一个矩形场地ABCD,其中AB=500米，AD=800米，顶点A,D为两个出口，现在想在货运广场内建一个货物堆放平台P,在BC边上（含B,C两点）开一个货物入口M,并修建三条专用车道PA,PD,PM.若修建每米专用车道的费用为10000元，当M,P建在何处时，修建专用车道的费用最少？最少费用为多少？（结果保留整数）
【课后训练】
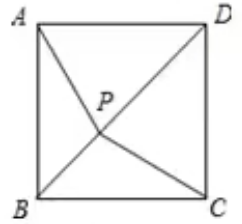
1.如图，P为正方形ABCD对角线BD上一动点，若AB=2,则AP+BP+CP的最小值为（）
A. +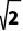
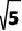
B. +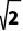
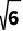
C. 4
D. 3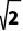
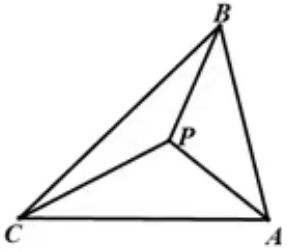
2.如图，点P为锐角ΔABC的费马点，且PA=3,PC=4,∠ABC=60°,则费马距离为 .
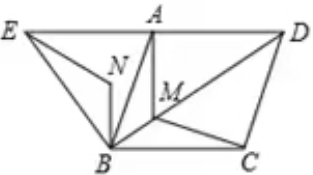
3.如图，四边形ABCD是菱形，AB=4,且∠ABC=∠ABE=60°,M为对角线BD(不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为 ．
4.若点P为ΔABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°,则点P叫做ΔABC的费马点．
（1)若P为锐角ΔABC的费马点，且∠ABC=60°,PA=3,PC=4,则PB的值为 ；
（2)如图，在锐角ΔABC的外侧作等边ΔACB',连结BB'.求证：BB'过ΔABC的费马点P,且BB'=PA+PB＋PC.
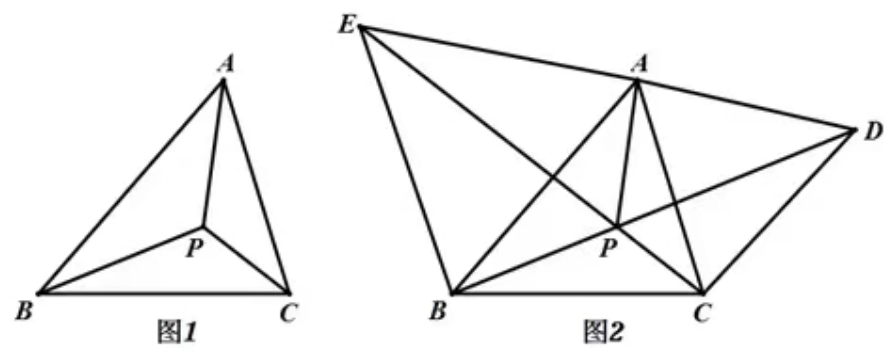
5.如图1,P为ΔABC所在平面上一点，且∠APB=∠BPC=∠CPA=120°,则点P叫做ΔABC的费马点：
（1)若点P是等边三角形三条中线的交点，点P (填是或不是）该三角形的费马点；
（2)如果点P为锐角ΔABC的费马点，且∠ABC=60°,求证：ΔABP∽ΔBCP;
（3)已知锐角ΔABC,分别以AB、AC为边向外作正ΔABE和正ΔACD,CE和BD相交于P点，如图2,①求∠CPD的度数；②求证：P点为ΔABC的费马点。
数学陈老师:
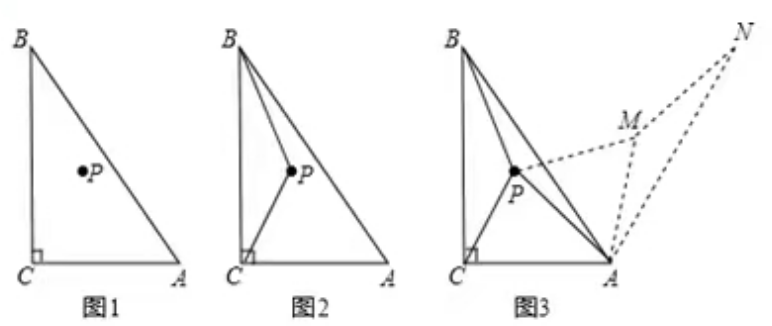
6.如图1,在ΔABC中，∠ACB=90°,点P为ΔABC内一点．
（1)连接PB,PC,将ΔBCP沿射线CA方向平移，得到ΔDAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意，请在图2中补全图形；
②如果BP⊥CE,BP=3,AB=6,求CE的长
（2)如图3,以点A为旋转中心，将ΔABP顺时针旋转60°得到ΔAMN,连接PA、PB、PC,当AC=3,AB=6时，根据此图求PA+PB+PC的最小值．
【答案】
【分析】创作不易
【详解】赞赏后有解析过程
点赞+关注
学习不迷路
