
学霸数学,让你更优秀!
(2024龙华区中考二模)如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,连接BE,作∠BEF=120°交CD边于点F,若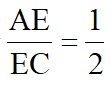 ,则
,则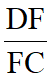 的值为( ),
的值为( ),
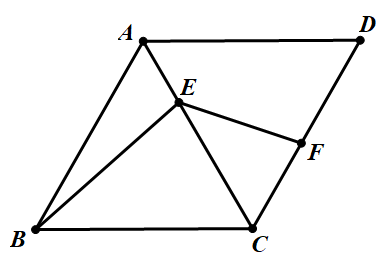
以下四种方法中都设AB=6
方法一:利用平行线构造相似
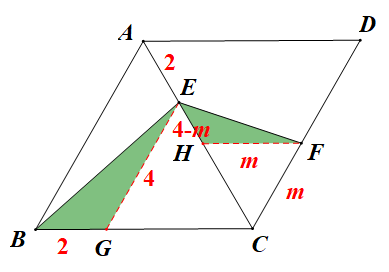
过点E作EG||AB交BC于点G,过点F作FH||AD交AC于点H,易知△ECG和△HFC都为等边三角形,由∠BEF=120°,∠BEC=60°故∠BEG+∠FEH=60°,而∠BEG+∠GBE=60°得∠GBE=∠HEF,同时∠BGE=∠EHF=120°得△BEG~△EFH,设CF=m,则EH=4-m,BG=AE=2,EG=4,得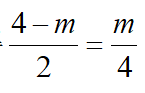 得m=
得m=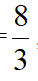 ,DF=
,DF=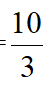 ,故
,故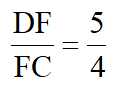 ,选D方法二:特点等分点构造子母型相似
,选D方法二:特点等分点构造子母型相似
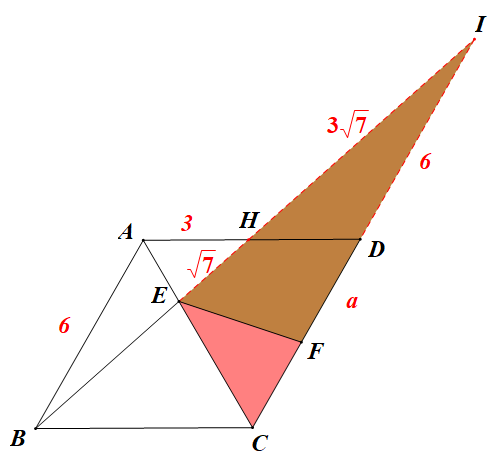
延长BE交CD延长线于点I,交AD于点H,易知AH=3,H为AD中点,故DI=6,∠FEI=∠ECI=60°得△IEF~△ICE,易知EI=4设DF=a,则有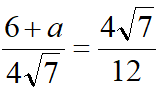 得a=
得a=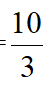 得CF=
得CF=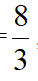 ,故
,故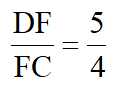 ,选D
,选D
方法三:平行等分构造相似
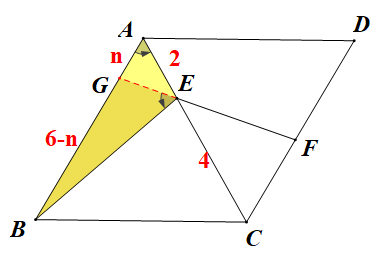
BAE=60°得△BEG~△BAE,设AG=n,则AG=6-n,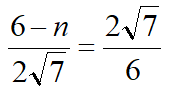 得n=
得n=
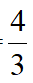
,故CF=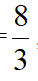 ,DF=
,DF=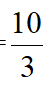 ,故
,故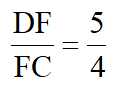 选D
选D
方法四:全等+相似
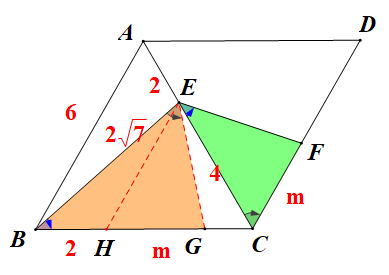
过点E作EH||AB,同时作∠BEF的平分线交BC于点G,易知△ECF≌△EHG,△BEG~△ECF,设CF=m则GH=m,
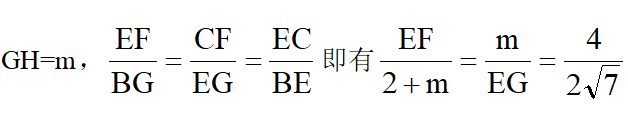
即有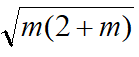 ,由EF=EG=代入可得m=
,由EF=EG=代入可得m=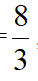 ,DF=
,DF=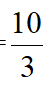 ,故
,故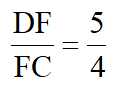 ,选D
,选D
点评:以上虽然有4种方法之多,但其核心方法是相同的,那就是构造相似,题目给的角度本身比较特殊,有比例但没有线段长,相似跑不了.
经过了不断的积累和沉淀,不断对中考数学题型的研究与总结,《中考压轴专题》隆重推出,帮助同学们提升实力.本书包含6个大专题,每个专题下包含多个考点和题型,力求覆盖所有压轴题型.题目取自中考真题、平时模拟真题中的压轴题、经典题,可帮助同学们精准训练,提升解题能力.
关于学霸数学
"学霸数学"专注于数学中考高考考试的最新信息,好题与压轴题解题技巧、知识专题分析以及考试分析与解答,考试动向及政策分析解读、家庭教育相关分享!如果您是家长或学生,对学习方面有任何问题,请联系小编!






