中考选择题热点考向:要知道△ABC的面积,只要知道...?

以“要知道特定的某区域面积，只需要知道某另一区域的面积”为题设是今年中考选择题压轴的热点方向，其所对的题型在省内各地模拟卷中频繁出现. 我挑选了赤城中学最近出现的一道题作分析. 

我们先用正常思路解题. 旋转前后的两矩形面积不变，减去公共部分S△BEC后，可得S △MEC＋S△NEB＋S长方形ANMD＝S梯形CFGB. 通过观察，我们可知S△MEC＋S△NEB＝S△BEC.

如图所示，过点C作CH垂直BG，交BG于点H. 

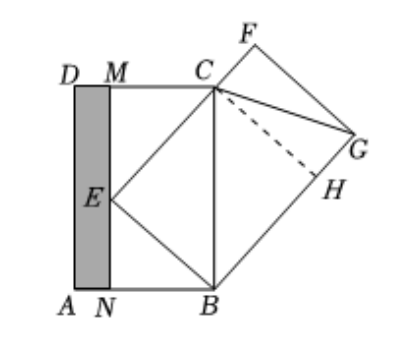
△辅助线示意图

易得S△BEC＝S△BHC，所以S△FCG＝1/2的S四边形CHGF=1/2的S矩形ANMD. 由此得到答案，要知道S矩形ANMD只需要知道S△CGF. 

当然，本题能挖掘的价值远不止于此. 

请同学们思考为什么要把S△ECM和S△EBN两个三角形面积放一起考虑?

因为这道题不仅没有指定矩形长和宽的值，甚至连长宽比都没有告诉我们，而长宽比决定了旋转角的大小，即ME：NE的值. 这就意味着不管是从绝对长度还是从相对比例上来看，阴影部分矩形面积都与其无关. 以B选项为例，在矩形长宽比未锁定的情况下，ME/EN的比值存在多种可能，我们显然无法用单一的S△ECM去恒定表示S矩形ANMD. 

请同学们再思考本题A、B选项能否如此考虑？

能.

A选项：S△BEC=1/2的S矩形BNMC，在长宽比未锁定的情况下，DM与MC的比例也无法锁定.既然无法锁定，就意味着存在多种可能，据此判定A选项错误.

B选项：S△BGC＝1/2的S矩形BEFC，若B选项正确，那么A选项也可推出，所以B选项也错误.