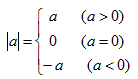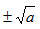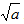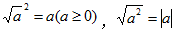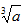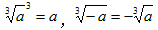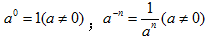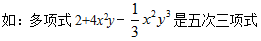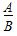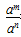一、实数与特殊角的三角函数值(每年2~4道,9~16分)
二、整式与因式分解(每年2~4道,7~10分)
三、分式(每年1~3题,3~13分)
四、二次根式(每年1~3题,3~12分)
在数学中考中,数与式部分主要考查实数及其运算、数的开方与二次根式、整式与因式分解、分式及其运算;而这些考点中,对实数包含的各种概念的运用的考察占了大多数,但是试题难度设置的并不大,属于中考中的基础“送分题”,题目多以选择题、填空题以及个别计算类简单解答题的形式出现;但是,由于数学题目出题的多变性,虽然考点相同,并不表示出题方向也相同,所以在复习时,需要考生对这部分的知识点的原理及变形都达到熟悉掌握,才能在众多的变形中,快速识别问题考点,拿下这部分基础分。
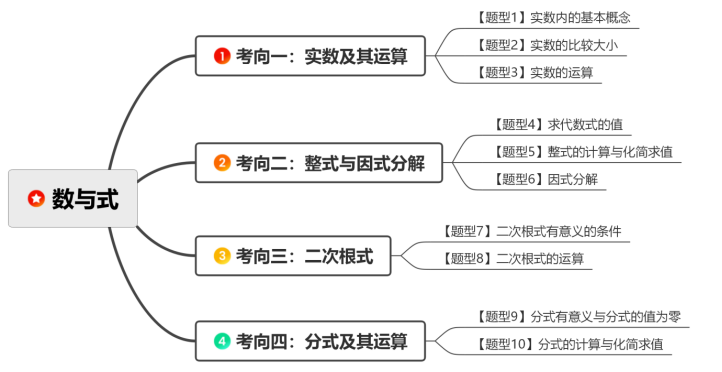
一、知识体系梳理
在数与式的学习过程中,与自然数的学习类似,都是要学习加、减、乘、除运算,在学习新知识的时候,注意概念的学习和理解,如有理数、实数,它们的定义方法类似,类比学习和记忆更高效。在数的学习中,有理数和实数都会涉及相反数、绝对值、数轴这些知识点,注意前后之间的联系,找出共同点和不同点。
在学习代数式的时候,注意深入理解用字母表示数的知识,理解这个本质之后,很多代数式的运算也就不那么难理解了,本质上还是数的运算。剩下的就是一些代数式中特有的概念,比如乘法公式、因式分解、二次根式有意义、分式有意义条件等知识。
在学习的时候我们先铺开面,把书读厚,然后经过知识结构梳理之后,把相同点和不同点归类,形成知识网络,就是把书读薄。
二、知识点整理
一、实数与二次根式
实 数 的 相 关 概 念 | 正数 | 大于0的数叫做正数 | 意义:表示具有相反意义的量 |
负数 | 在正数前面加上“-”号的数叫做负数 | ||
数轴 | 规定了原点、正方向和单位长度的直线叫做数轴 | ||
相反数 | 只有符号不同的两个数,叫做互为相反数 (1)若a,b互为相反数,则a+b=0; (2)0的相反数是0; (3)在数轴上,互为相反数的两个数对应的点到原点的距离相等. | ||
绝对值 | 数轴上点a与原点的距离叫做a的绝对值,记作|a| 绝对值具有非负性:
| ||
倒数 | 乘积为1的两个实数互为倒数 (1)ab=1⇔a,b互为倒数; (2)0没有倒数; (3)倒数等于它本身的数是1和-1. | ||
科学计数法 | 把一个数写成a×10n(其中1≤|a|<10,n为整数)的形式 | ||
无理数 | 无限不循环的小数叫做无理数 | ||
平方根 | ① 如果一个数的平方等于a,那么这个数叫做a的平方根,记作 ② 性质:正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根. | ||
算术平方根 | ① 如果一个正数的平方等于a,即x2=a,那么这个数x 叫做a的算术平方根,记作 ② 非负性: | ||
立方根 | ① 如果一个数的立方等于a,那么这个数就叫做a的立方根,记作 ② 性质:正数只有一个正的立方根;0的立方根是0;负数只有一个负的立方根. ③ | ||
零指数,负指数幂 |
| ||
非负数 | 1.常见的三种非负数:|a|≥0,a2≥0,≥0(a≥0). 2.非负数的性质: ① 非负数有最小值是零; ② 任意几个非负数的和仍为非负数; ③ 几个非负数的和为0,则每个非负数都等于0. | ||
实 数 的 分 类 | 按定义分 | 有理数 | 整数 |
分数 | |||
无理数 | 正无理数 | ||
负无理数 | |||
按正负分 | 正实数 | ||
0 | |||
负实数 | |||
实 数 的 运 算 | 加法 | 同号两数相加,取原来的符号。并把它们的绝对值相加。 |
异号两数相加,取绝对储较大的加数的符号,并用较大数的绝对值 减失较小数的绝对值。 | ||
减法 | 减去一个效等于加上这个数的相反数 | |
乘法 | 两数相乘,同号得正,异号得负,并把它们的绝对值相乘 | |
几个非零实数相乘。积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数有奇数个时,积为负 | ||
n个数相乘,有一个因数为0,积为0. | ||
除法 | 两数相除,同号得正,异号得负,并把它们的绝对值相除 | |
0除以任何一个不等于0的数都得0 | ||
乘方 | 几个相同因数的积的运算,叫做乘方,记作an(a≠0,n为正整数)开方与乘方互为逆运算 | |
运算顺序 | 分级:加减是一级运算。除是二级运算,乘方和开方是三级运算,三级运算的题序是三二一、(如果有括号,先算括号内的;如果没有括号,在同一级运算中,要从左至右进行运算,无论何种运算,都要注意先定符号后运算) |
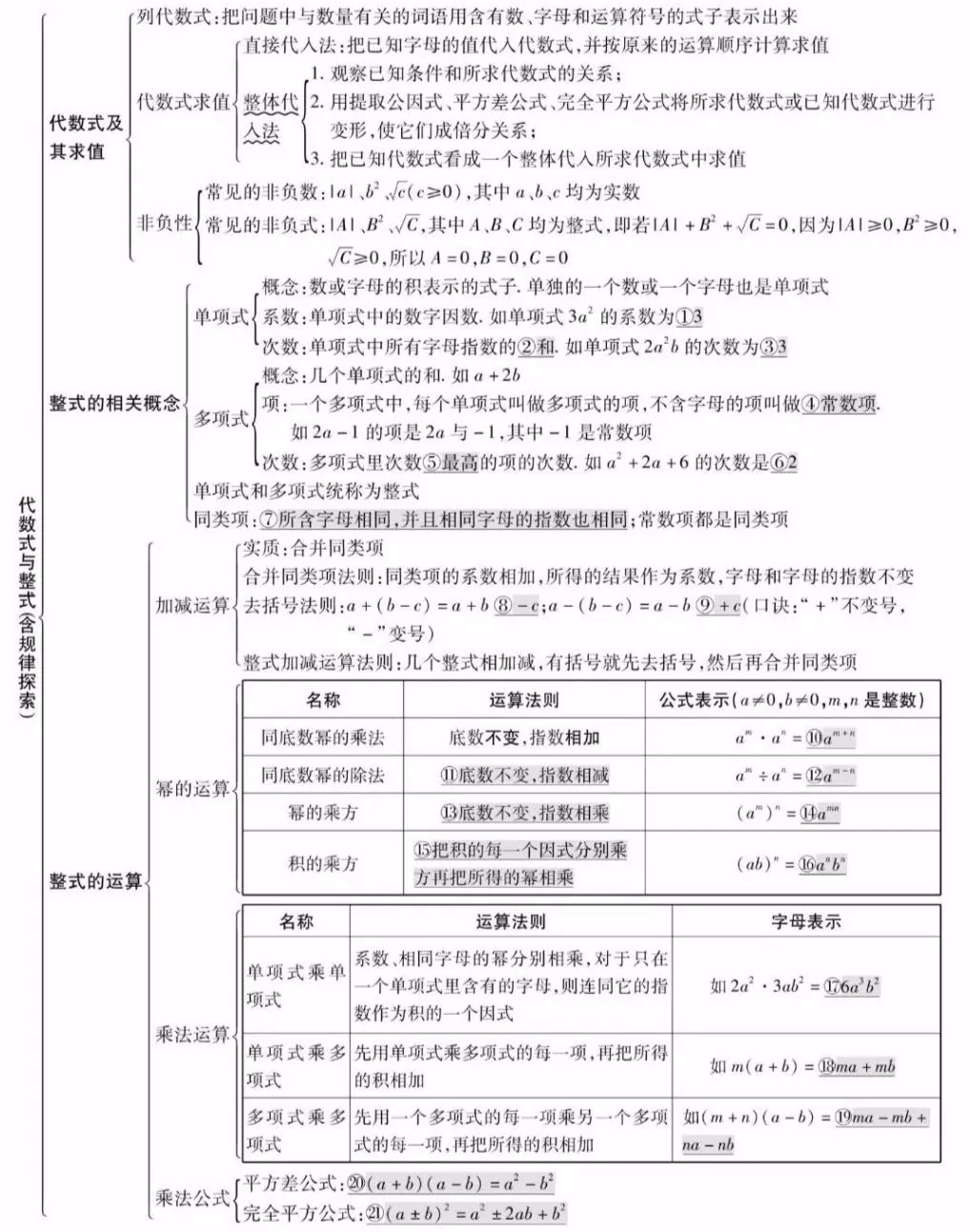
二、整式与分式
整 式 的 相 关 概 念 | 单项式 | 由数字或字母的乘积组成的式子;单项式中的数字因数叫做单项式的系数;单项式中所有字母指数的和叫做单项式的次数。 |
多项式 | 几个单项式的和叫做多项式;多项式中,每一个单项式叫做多项式的项,其中不含字母的项叫做常数项;多项式中次数最高项的次数就是这个多项式的次数。 | |
整式 | 整式是单项式与多项式的统称。 | |
同类项 | 所含字母相同,并且相同字母的指数也分别相同的单项式叫做同类项。 | |
合并同类项 | 把多项式中的同类项合并成一项叫做合并同类项,合并的法则是系数相加,所得的结果作为合并后的系数,字母和字母的指数不变。 | |
分 式 的 相 关 概 念 | 分式概念 | 形如 |
有意义的 条件 | 因为0不能做除数,所以在分式 | |
值为0 | 在分式 | |
分式的基本性质 | 分式的分子与分母同乘(或除以)一个不等于零的整式,分式的值不变.用式子表示是:
| |
约分 | 将分子、分母中的公因式约去,叫做分式的约分 | |
通分 | 将几个异分母的分式化为同分母的分式,这种变形叫分式的通分 |
整 式 运 算 | 幂 的 运 算 | 同底数幂乘法 | am·an=am+n(a≠0) | am+n=am·an | |
同底数幂除法 |
| am-n= | |||
幂的乘方 | (am)n=amn(a≠0) | amn=(am)n | |||
积的乘方 | (ab)n=anbn | anbn=(ab)n | |||
乘法 公式 | 平方差公式 | (a+b)(a-b)=a2-b2 | a2-b2=(a+b)(a-b) | ||
完全平方公式 | (a±b)2=a2±2ab+b2 | a2±2ab+b2=(a±b)2 | |||
整式 加减 | ① 整式的加减其实就是合并同类项; ② 整式加减的步骤:有括号,先去括号;有同类项,再合并同类项.注意去括号时,如果括号前面是负号,括号里各项的符号要变号. | ||||
整式 乘法 | ① 单项式与单项式相乘:把系数、同底数幂分别相乘,作为积的因式,只在一个单项式里含有的字母,则连同它的指数作为积的一个因式. ② 单项式与多项式相乘:m(a+b+c)=ma+mb+mC. ③ 多项式与多项式相乘:(m+n)(a+b)=ma+mb+na+nb. | ||||
整式 除法 | ① 单项式除以单项式:把系数、同底数幂相除,作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式. ② 多项式除以单项式:(a+b)÷m=a÷m+b÷m. | ||||
因式 分解 | 概念 | 把一个多项式化成几个整式的积的形式,叫做多项式的因式分解。和的形式变积的形式 | |||
因式分解方法 | 提公因 式法 | ma+mb+mc=m(a+b+c)(乘法分配律的运用) | |||
公式法 | ① 运用平方差公式:a2-b2=(a+b)(a-b). ② 运用完全平方公式:a2±2ab+b2=(a±b)2. | ||||
求代数式的值 | 1.一般地,用数值代替代数式里的字母,按照代数式指明的运算关系计算出的结果就叫做代数式的值. 2.求代数式的值的基本步骤: ① 代入:一般情况下,先对代数式进行化简,再将数值代入; ② 计算:按代数式指明的运算关系计算出结果. | ||||
分 式 运 算 | 分式加减 |
| |||
分式乘除 |
| ||||
分式的混合运算 | 在分式的加减乘除混合运算中,应先算乘除,进行约分化简后,再进行加减运算,遇到有括号的,先算括号里面的.运算结果必须是最简分式或整式. | ||||
三、易出错知识点
因式分解专题
易错点:
1.未能正确理解因式分解的定义:因式分解是将一个多项式表示为几个整式的积的形式。学生需要明确理解这一概念,才能正确进行因式分解。
2.提公因式时系数提取错误:在进行因式分解时,需要找出各项系数的最大公约数,并提取出来作为公因式。如果学生在此过程中出现错误,就会影响因式分解的结果。
3.漏掉常数项:在进行提公因式时,学生可能会忽略常数项。这是常见的错误,因为常数项在多项式中容易被忽视。
4.未能正确应用公式:在因式分解中,一些特定的多项式可以通过应用公式进行分解。如果学生未能正确应用这些公式,就会导致因式分解的结果不正确。
5.混淆了因式分解与整式的乘法:因式分解与整式的乘法是两个不同的概念。学生需要明确区分两者,以免在解题过程中出现混淆。
6.未能正确判断能否进行因式分解:对于一些多项式,可能无法进行因式分解。学生需要学会判断哪些多项式可以进行因式分解,哪些不能。
四、专项练习过关训练






五、思维导图
1、实数

2 、代数与整式(含规律探索)

3 、分式

4 、二次根式

在学习中改变,在改变中成长
电子版领取方式

第一步:点一点右下角的赞和在看
第二步:关注“升学题库”公众号
第三步:在公众号对话框发送 数与式

资料收集整理发布实属不易
点赞在看收藏分享以资鼓励



资料收集整理发布实属不易
点赞在看收藏分享以资鼓励
【温馨提示】:做题的意义并不在于做题本身,而是在于强化对所学知识的理解和运用能力,务必将每道题弄懂吃透!