01
知识技能梳理
01
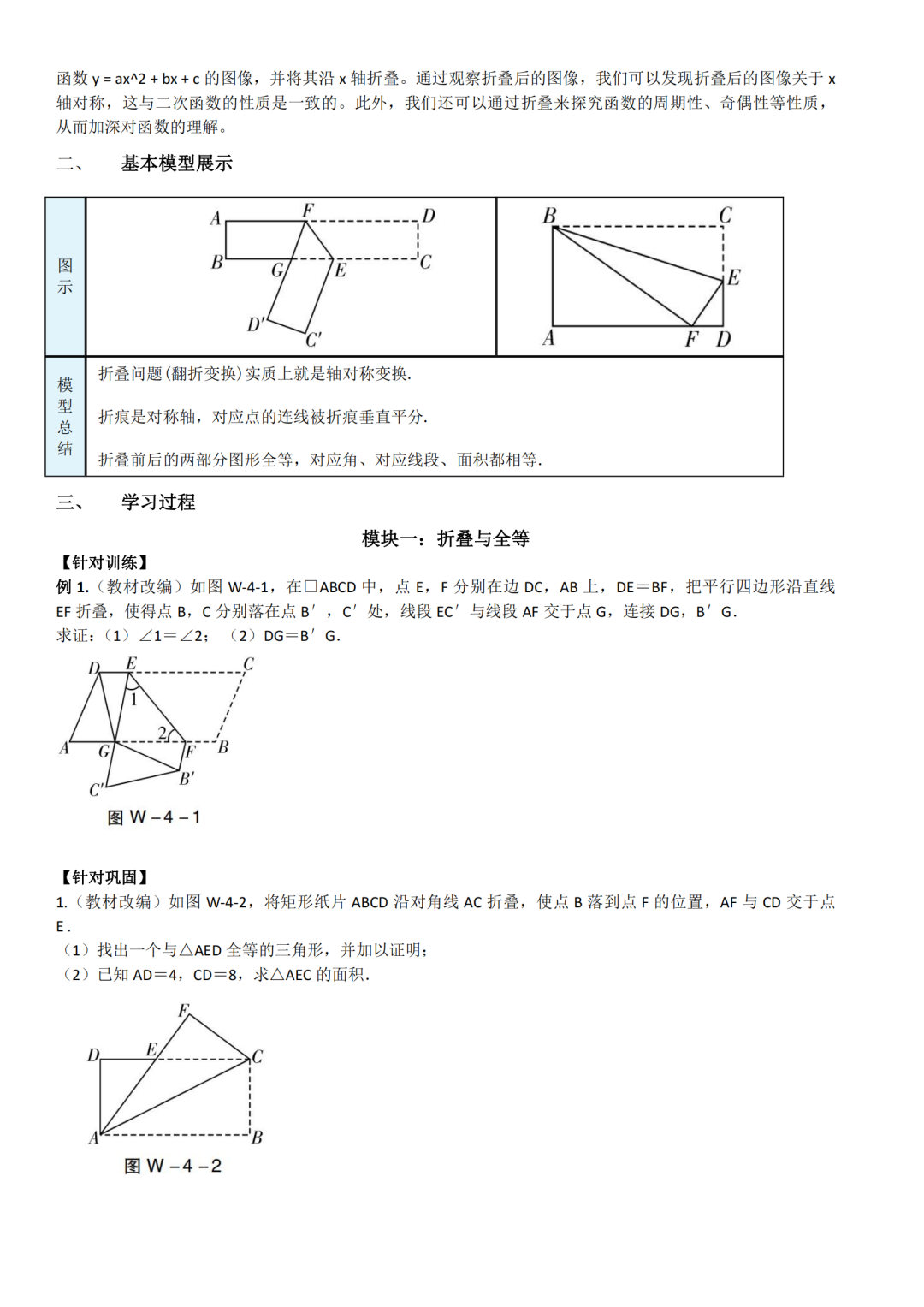
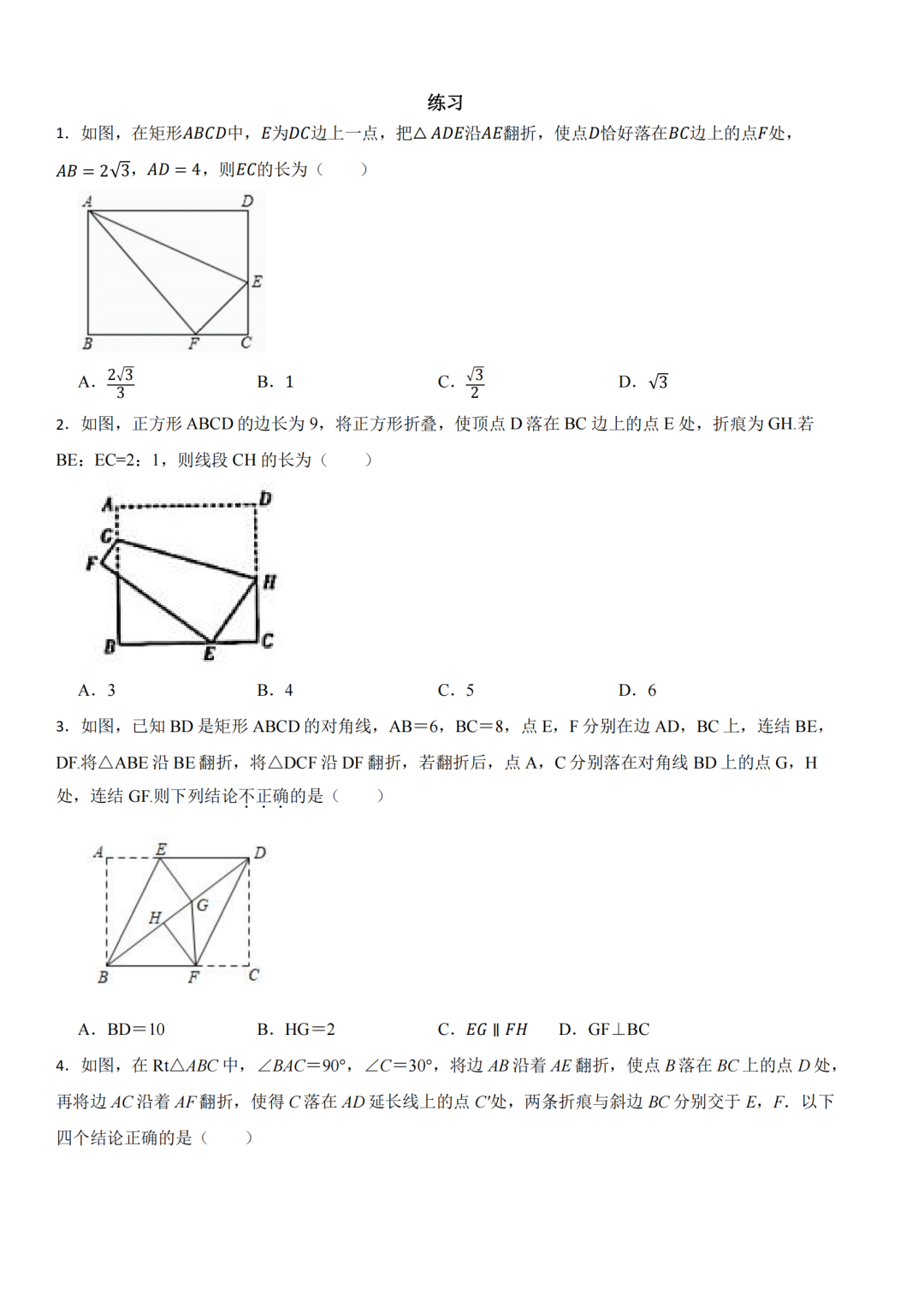
模块一:折叠与全等
折叠是一种基本的几何变换,指的是将一个平面图形或物体沿着一条直线或一条线段进行对折,从而得到一个对称的图形或缩小其占用空间的过程。折叠过程中,图形的面积和形状保持不变,这体现了折叠的基本性质。折叠不仅在数学中有应用,在实际生活中也常用于减少物品或物体的占用空间,便于储存和携带。
折叠与全等,有着紧密的联系。通过折叠,我们可以得到全等的图形;同时,全等图形的性质也可以在折叠中得到验证和应用。在学习和理解这两个概念的过程中,我们可以培养自己的逻辑思维和空间想象能力,为未来的数学学习和实际应用打下坚实的基础。折叠与全等的关系十分密切。折叠操作实质上是全等变换,这意味着折叠后的图形与原图形是全等的。在这个过程中,我们需要注意因折叠而形成的等线段、等角,这些相等关系是解决问题的关键。
具体来说,当我们将一个图形进行折叠时,位于折痕两侧的图形关于折痕形成轴对称图形,这意味着这些部分在形状和大小上都是完全相同的,即它们全等。这种全等性不仅体现在图形的整体形态上,还体现在图形的各个部分,包括对应边、角、线段、周长、面积等都相等。此外,折叠前后,对应点的连线被折痕垂直平分,这也是全等性的一个重要体现。
因此,我们可以说折叠是全等变换的一种形式,它帮助我们理解和分析图形的全等性质。通过折叠操作,我们可以更直观地理解全等概念,并学会利用全等性质解决相关问题。
02
模块二:折叠与相似
相似则是指两个图形的形状相同但大小不同,且它们的对应边的比值是相等的。如果两个图形是相似的,我们可以通过一些变换,如平移、旋转、镜像和相似比例变换,将一个图形变换成另一个图形。
当谈到折叠与相似的关系时,可以想象一个图形经过折叠后可能会形成另一个与之相似的图形。例如,在纸张折叠艺术中,经常通过折叠纸张得到不同形状和大小的相似图形。这种折叠过程实际上就是一种特殊的相似变换,通过折叠操作,原始图形被变换成与其相似的图形。
总的来说,折叠和相似都是几何学中重要的概念,它们之间存在密切的关系。折叠可以实现图形的对称变换和空间优化,而相似则关注图形形状的不变性及其在变换中的保持。在实际应用中,折叠与相似的概念常常相互结合,共同用于创造和设计各种几何图形和物体。
03
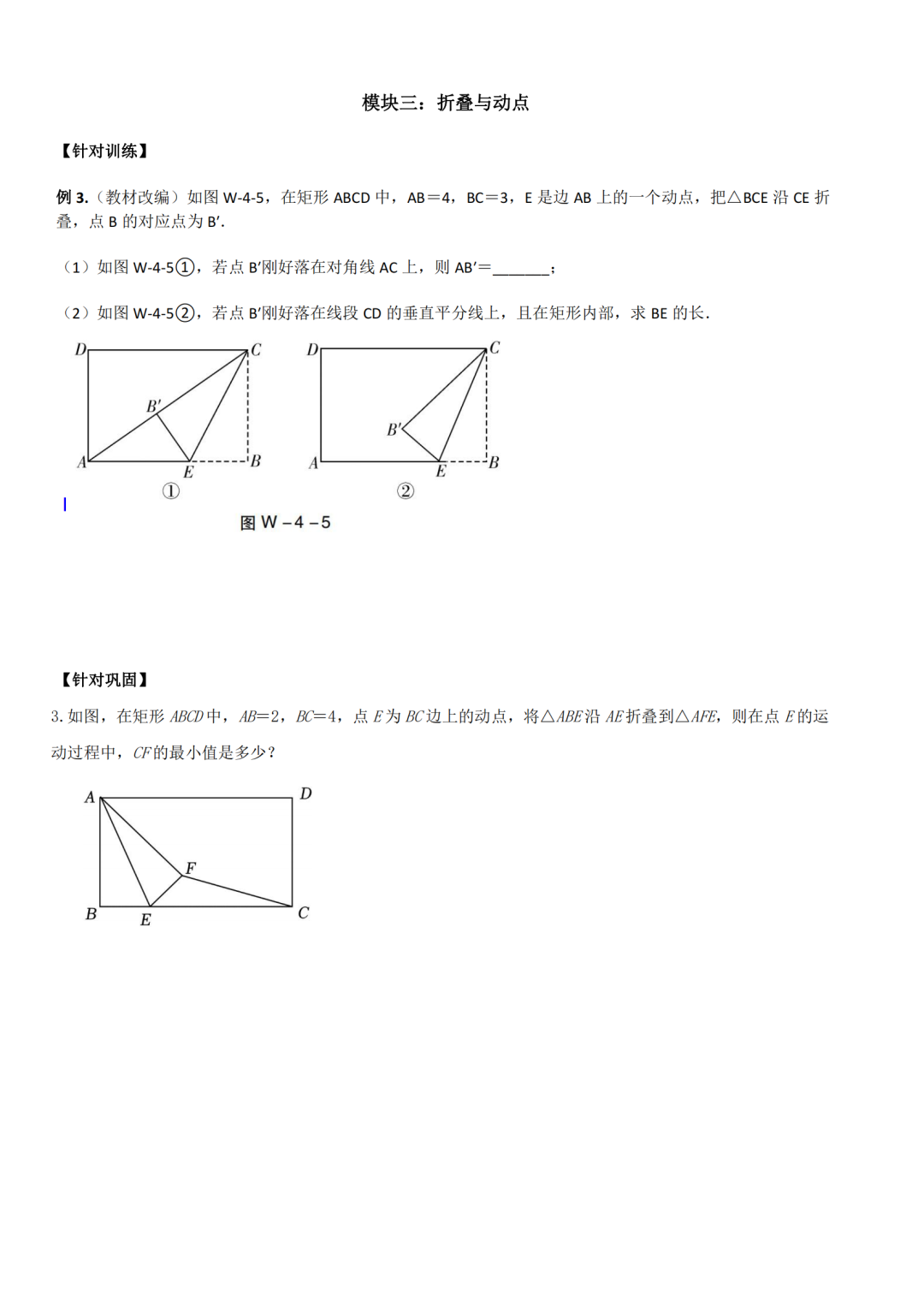
模块三:折叠与动点
折叠与动点之间存在一定的关系,特别是在涉及图形变换和动态几何问题的场景中。
首先,折叠是一种几何变换,它涉及到图形的对称性和空间位置的改变。当图形发生折叠时,其形状和某些属性(如面积)可能保持不变,但位置关系会发生变化。这种变化对于理解和分析动点的行为至关重要。
动点是在几何图形中随时间或条件变化而移动的点。它的位置、速度和方向都可能不断变化。在涉及折叠的几何问题中,动点可能会受到折叠操作的影响,从而改变其原有的运动轨迹或速度。
具体来说,当图形发生折叠时,动点可能随之移动到新的位置。折叠操作可能改变动点与其他点或线段的相对位置关系,进而影响到动点的运动状态。例如,在某些问题中,动点可能在折叠过程中从图形的一侧移动到另一侧,或者其运动方向可能因折叠而发生改变。
此外,折叠还可能影响到动点所处的图形的形状和属性。当图形折叠时,其对称性可能发生变化,从而影响到动点的位置和运动轨迹。这种影响在解决涉及折叠和动点的几何问题时需要特别考虑。
综上所述,折叠与动点之间存在密切的关系。折叠操作可以影响动点的位置、速度和运动轨迹,而动点的行为也可能受到折叠操作的影响。因此,在解决涉及折叠和动点的几何问题时,需要综合考虑这两个
04
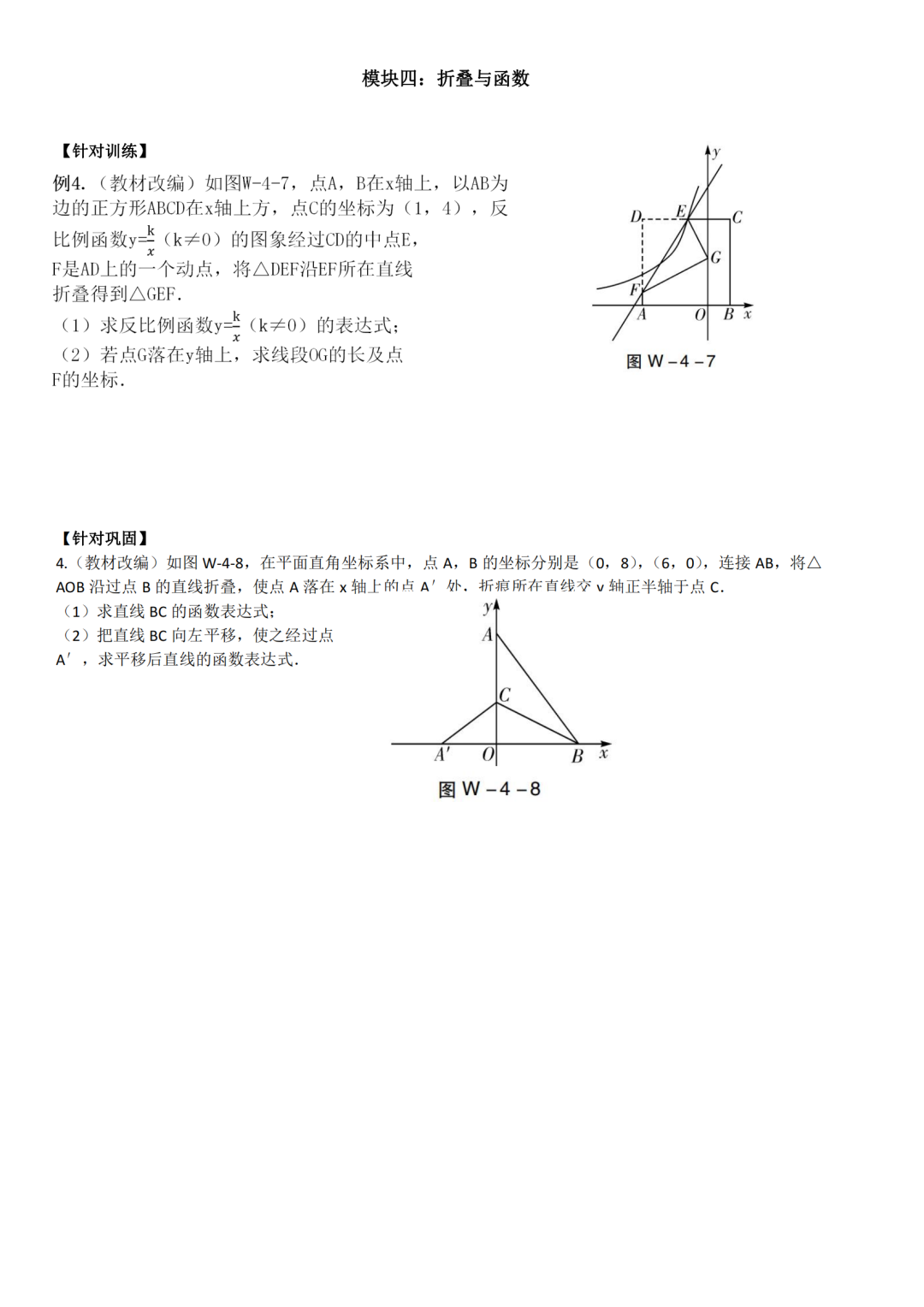
模块四:折叠与函数
折叠与函数的关系:在数学中,函数是一种特殊的对应关系,它描述了自变量与因变量之间的关系。折叠与函数之间存在着密切的关系。我们可以通过折叠来探究函数的性质,也可以通过函数来描述折叠的规律。例如,当我们将一个图形沿x轴折叠时,对应的y值会发生变化,这种变化可以用函数来描述。通过折叠与函数的结合,我们可以更深入地理解函数的性质和应用。
为了更好地理解折叠与函数的关系,我们可以通过一些实例来进行探究。例如,我们可以考虑一个二次函数y = ax^2 + bx + c的图像,并将其沿x轴折叠。通过观察折叠后的图像,我们可以发现折叠后的图像关于x轴对称,这与二次函数的性质是一致的。此外,我们还可以通过折叠来探究函数的周期性、奇偶性等性质,从而加深对函数的理解。
02
自主学习单
左右滑动,查看更多
03
详解答案
左右滑动,查看更多
04
老师讲解视频
01
模块一
02
模块二
03
模块三
04
模块四
05
授课教师简介

授课教师简介:唐晓婕
深圳市罗湖区翠园实验学校数学科组长
省首届基础教育优质课一等奖
市级优秀班主任
市级命题比赛一等奖
作为主持人或主要成员参与省、市、区各级课题
全国中学生数学能力测评优秀指导老师
06
罗湖区中考备考“百师助学”课程简介
为帮助学生学好数学,引导教师高效备考,2024年,罗湖区教育科学研究院开展中考备考“百师助学”活动,初中数学学科组织优秀教师开发了十八个专题的中考备考“百师助学”课程样例,供全区初三数学教师教学参考和学生自主学习;也欢迎各学校邀请他们到学校授课。
序号 | 助学专题名称 | 单位 |
第一讲:(几何基础专题1) | 中考作图题 | 桂园中学郭培香 |
第二讲:(几何基础专题2) | 中点常见问题及辅助线作法 | 翠园实验学校黄缨 |
第三讲:(对称相关专题1) | 将军饮马与最值问题 | 红桂中学陈伟钊 |
第四讲:(对称相关专题2) | 角平分线相关问题的应对策略 | 桂园中学余阳 |
第五讲:(对称相关专题3) | 等腰三角形相关题型 | 翠园实验学校段艳慈 |
第六讲:(对称相关专题4) | 折叠问题 | 翠园实验学校唐晓婕 |
第七讲:(面积相关问题专题1) | 面积与等面积法在中考试题中的应用 | 罗湖外语初中学校张利民 |
第八讲:(面积相关问题专题2) | 用平行线解函数中三角形面积问题 | 罗湖外语初中学校黄永稳 |
第九讲:(面积相关问题专题3) | 反比例函数的k值问题 | 罗湖实验学校周刚山 |
第十讲:(相似多边形相关专题1) | 求线段比问题 | 布心中学刘蕊 |
第十一讲:(相似多边形相关专题2) | 一线三等角模型 | 罗湖实验学校熊梦玲 |
第十二讲:(相似多边形相关专题3) | 平行构造相似 | 滨河实验中学蒋沅润 |
第十三讲:(函数相关专题1) | 一、二次函数与反比例函数应用题 | 罗湖外语初中学校任平 |
第十四讲:(常见数学模型专题1) | 手拉手模型常用结论的证明和应用 | 桂园中学苏剑平 |
第十五讲:(常见数学模型专题2) | 相似三角形的共边共角模型 | 滨河实验中学林翠凤 |
第十六讲:(常见数学模型专题3) | 对角互补模型(全等,相似,圆) | 翠园东晓中学曾秀娟 |
第十七讲:(常见数学模型专题4) | 45度角问题处理策略——构造半角模型 | 布心中学段玲 |
第十八讲:(常见数学模型专题5) | 隐圆模型 | 翠园东晓创新学校吕永生 |
07
罗湖区中考备考“攻坚课程”推荐
为帮助学生学好数学,引导教师高效备考,2023年罗湖区教育科学研究院初中数学学科,针对中考的重难点开展备考指导活动。组织本区优秀教师开发了十个专题的“备考攻坚课程”样例。并开展备考攻坚课程教学,现公开“教学素材”,供全区初三数学教师参考和学生自主学习。
每个专题的“教学素材”包含:(1)教学设计、(2)自主学习单、(3)详细答案、(4)授课PPT和(5)上课视频五个部分内容。各专题的“教学素材”可以在罗湖教育信息网上的“初中数学教与学”网站下载。下载网址:http://czshuxue.luohuedu.net/m/new/2109-0-0-1
所有“攻坚课程”在本公众号都有推文,推文以方便学生自主学习的形式制作,欢迎关注使用。
欢迎各校邀请课程开发老师到本校开展“备考攻坚课程”教学。
序号 | 攻坚专题名称 | 负责人 |
第一讲(选择题难点突破1) | 图形变换与二次函数中的多结论问题 | 滨河实验中学林翠凤 |
第二讲(选择题难点突破2) | 几何图形轨迹(最值)问题 | 罗湖外语初中学校邓雪玲 |
第三讲(填空题难点突破1) | 反比例函数K值的有关计算 | 翠园初级中学秦晓莉 |
第四讲(填空题难点突破2) | 计算中的图形构建 | 布心中学崔景晓 |
第五讲(压轴题难点突破1) | 利用平行线解决二次函数中的面积问题 | 罗湖外语初中学校郭爱玲 |
第六讲(压轴题难点突破2) | 函数性质应用探究题 | 布心中学崔景晓 |
第七讲(压轴题难点突破3) | 隐圆问题 | 桂园中学刘清丽 |
第八讲(压轴题难点突破4) | 发现类比探究题 | 罗湖外语初中学校吴丹妮 |
第九讲(压轴题难点突破5) | 新定义型阅读理解题 | 罗湖外语实验王少萍 |
第十讲(压轴题难点突破6) | 与几何变换相关的探究题 | 桂园中学罗国浩 |
文字:深圳市罗湖区翠园实验学校 唐晓婕
制作:深圳市罗湖区翠园实验学校 唐晓婕
审核:洪飞