中考数学冲刺复习之二次函数平移问题
中考数学冲刺复习
重难点题型突破
二次函数平移问题
二次函数中的平移、翻折、对称、旋转、折叠问题，是中考综合题常考点，难点。为帮助同学们更好的掌握和应用该知识点，我们近期分类进行讲解，请同学们持续关注学习。
【目录】重难点题型突破
题型01 二次函数平移问题
题型02 二次函数翻折问题
题型03 二次函数对称问题
题型04 二次函数旋转问题
题型05 二次函数折叠问题
重难点题型突破
题型01
二次函数平移问题
1、二次函数的平移变换
2.平移与增加性变化
如果平移后对称轴不发生变化，则不影响增减性，但会改变函数最大（小）值。
只对二次函数上下平移，不改变增减性，改变最值。
只对二次函数左右平移，改变增减性，不改变最值。
题目1.已知在平面直角坐标系xOy中，抛物线y=ax2-2ax-3(a≠0)与x轴交于点A、点B(点A在点B的左侧），与y轴交于点C,抛物线的顶点为D,且AB=4.
（1)求抛物线的表达式：
（2)点P是线段BC上一点，如果∠PAC=45°,求点P的坐标；
（3)在第（2)小题的条件下，将该抛物线向左平移，点D平移至点E处，过点E作EF⊥直线AP,垂足为点F,如果tan∠PEF=1/2，求平移后抛物线的表达式。
【答案】
（1)y=x2-2x-3
（2) P (5/3, -4/3)
（3) y= (x+17/9) 2-4
【分析】
（1)设点A的横坐标为xA,点B的横坐标为xB ,根据对称轴，AB=4,列式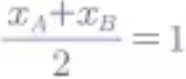
，（xB+xA）/2=1，xB-xA=4利用根与系数关系计算确定a值即可。
（2)过点C作AC⊥MN于点C,交AC右侧的AP的延长线于点M,交AC左侧的AP的延长线于点N,利用三角形全等，确定坐标，后根据解析式交点确定所求坐标即可.
（3)设抛物线向左平移了t个单位，则点E(1-t,-4),过点F作x轴的平行线交过点P和y轴的平行线于点H,交过点E和y轴的平行线于点G,证明RtΔFGE∽RtΔPHF,根据相似三角形的性质得出GE/HF=GF/HP=EF/FP=1/tan∠PEF=2即可求解.
数学陈老师:
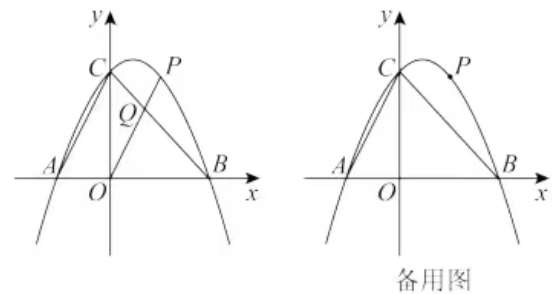
题目2.如图1,抛物线y=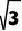
/6x2+4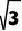/3x+2与x轴交于点A,B(A在B左边），与y轴交于点C,连AC,点D与点C关于抛物线的对称轴对称，过点D作DE//AC交抛物线于点E,交y轴于点P.
（1)点F是直线AC下方抛物线上点一动点，连DF交AC于点G,连EG,当ΔEFG的面积的最大值时，直线DE上有一动点M,直线AC上有一动点N,满足MN⊥AC,连GM,NO,求GM+MN+NO的最小值；
（2)如图2,在（1)的条件下，过点F作FH⊥x轴于点H交AC于点L,将ΔAHL沿着射线AC平移到点A与点C重合，从而得到ΔA'H'L'(点A,H,L分别对应点A',H',L'),再将ΔA'H'L'绕点H'逆时针旋转α(00＜a＜180°),旋转过程中，边A'L'所在直线交直线DE于Q,交y轴于点R,求当ΔPQR为等腰三角形时，直接写出PR的长。
数学陈老师:
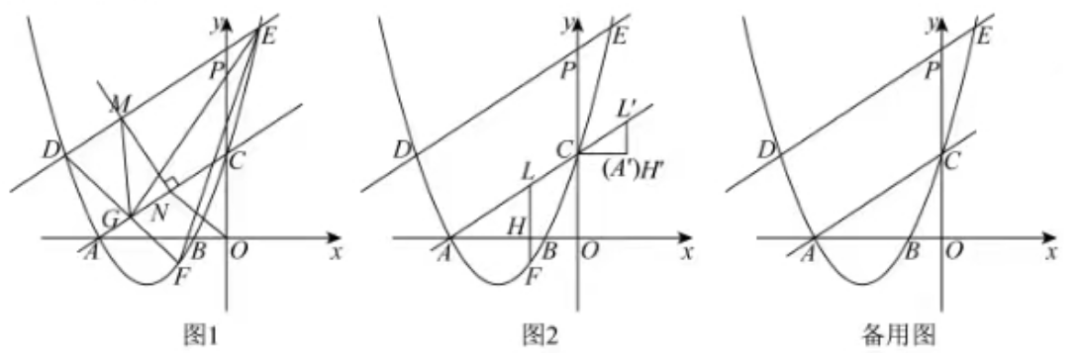
题目3. 如图，在平面直角坐标系中，抛物线y=-1/2x2+bx+c与x轴交于A(-2,0),B(4, 0)两点（点A在点B的左侧），与y轴交于点C,连接AC、BC,点P为直线BC上方抛物线上一动点，连接OP交BC于点Q.
（1)求抛物线的函数表达式；
（2)当PQ/OQ的值最大时，求点P的坐标和PQ/OQ的最大值；
（3)把抛物线y=-1/2x2+bx+c沿射线AC方向平移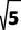
个单位得新抛物线y',M是新抛物线上一点，N是新抛物线对称轴上一点，当以M、N、B、C为顶点的四边形是平行四边形时，直接写出N点的坐标，并把求其中一个N点坐标的过程写出来。
数学陈老师:
题目4.坐标综合：
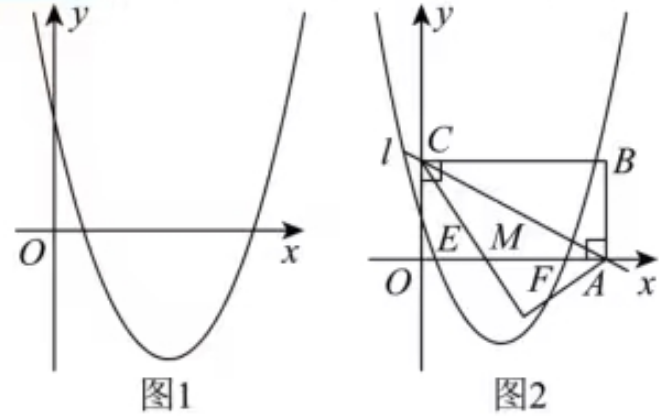
（1)平面直角坐标系中，抛物线C1:y1 =x2+bx+c的对称轴为直线x=3,且经过点（6, 3),求抛物线C1的解析式，并写出其顶点坐标；
（2)将抛物线C1在平面直角坐标系内作某种平移，得到一条新的抛物线C2:y2=x2-2mx+㎡-1,
①如图1,设自变量x在1≤x≤2的范围内取值时，函数y2的最小值始终等于－1.此时，若y2的最大值比最小值大1/2m,求m的值；
②如图2,直线l:y=-1/2x+n(n＞0)与x轴、y轴分别交于A、C两点．过点A、点C分别作两坐标轴的平行线，两平行线在第一象限内交于点B.设抛物线C2与x轴交于E、F两点（点E在左边）．现将图中的ΔCBA沿直线l折叠，折叠后的BC边与x轴交于点M.当8≤n≤12时，若要使点M始终能够落在线段EF(包括两端点）上，请通过计算加以说明：抛物线C1在向抛物线C2平移时，沿x轴的方向上需要向左还是向右平移？最少要平移几个单位？最多能平移几个单位？
数学陈老师:
题目5. 如图1,在平面直角坐标系xOy中，二次函数y=x2-4x+c的图象与y轴的交点坐标为（0, 5),图象的顶点为M.矩形ABCD的顶点D与原点O重合，顶点A,C分别在x轴，y轴上，顶点B的坐标为（1, 5).
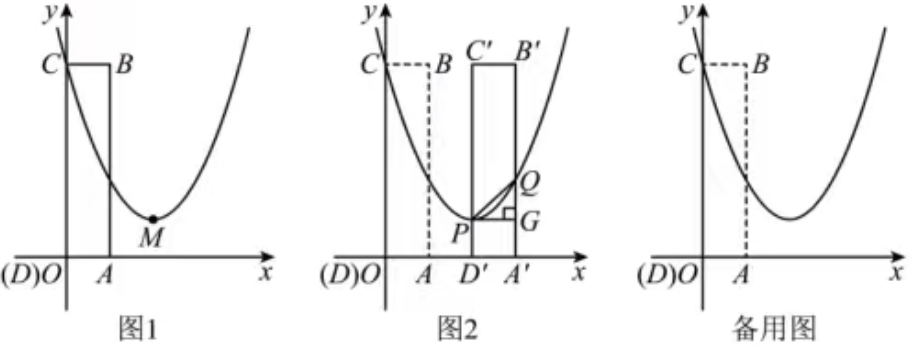
（1)求c的值及顶点M的坐标;
（2)如图2,将矩形ABCD沿x轴正方向平移t个单位（0＜t＜3)得到对应的矩形A'B'C'D'.已知边C'D',A'B'分别与函数y=x2-4x+c的图象交于点P,Q,连接PQ,过点P作PG⊥A'B'于点G.
①当t=2时，求QG的长；
②当点G与点Q不重合时，是否存在这样的t,使得ΔPGQ的面积为1?若存在，求出此时t的值：若不存在，请说明理由。
数学陈老师:
题目6.如图，二次函数y=1/2x2+bx-4的图像与x轴相交于点A(-2, 0)、B,其
顶点是C.
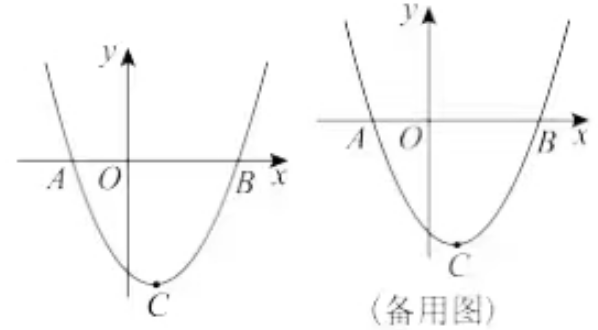
（1) b= ;
（2)D是第三象限抛物线上的一点，连接OD,tan∠AOD=5/2; 将原抛物线向左平移，使平移后的抛物线过点D,过点（k,0)作x轴的垂线l.已知在l的左侧，平移前后的两条抛物线都下降，求k的取值范围；
（3)将原抛物线平移，平移后的抛物线与原抛物线的对称轴相交于点Q,且其顶点P落在原抛物线上，连接PC、QC、PQ. 已知ΔPCQ是直角三角形，求点P的坐标。
数学陈老师:
题目7.如图，过原点的抛物线y1=ax(x-2n)(a≠0,a,n为常数）与x轴交于另一点A,B是线段OA的中点，B(-4, 0),点M(-3, 3)在抛物线y上．
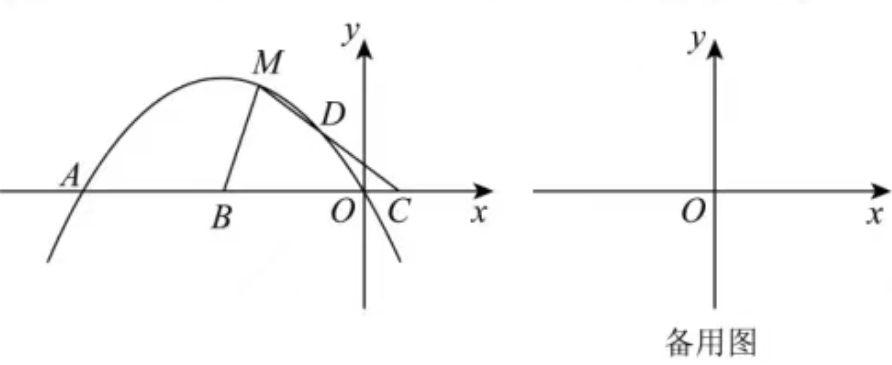
（1)点A的坐标为 ；
（2)C为x轴正半轴上一点，且CM=CB.
①求线段BC的长；
②线段CM与抛物线y1相交于另一点D,求点D的坐标；
（3)将抛物线y1向右平移（4-t)个单位长度，再向下平移16/5个单位长度得到抛物线y2,P,Q是抛物线y2上两点，T是抛物线y2的顶点．对于每一个确定的t值，求证：矩形TPNQ的对角线PQ必过一定点R,并求出此时线段TR的长。
【答案】
【分析】创作不易
【详解】赞赏后有解析过程
点赞+关注
学习不迷路
