中考数学冲刺复习之反比例函数与几何综合

中考数学冲刺复习之反比例函数与几何综合

中考数学冲刺复习

反比例函数

与几何综合

【题型探究1】反比例函数与全等三角形

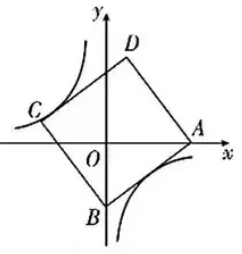
1.如图，正方形ABCD的边长为5,点A的坐标为（4, 0),点B在y轴上，若反比例函数y=k/x（k≠0)的图象过点C,则k的值为(  ).

    A. 4 

    B. -4

    C. -3

    D. 3

【题型探究2】 反比例函数与最短路径    

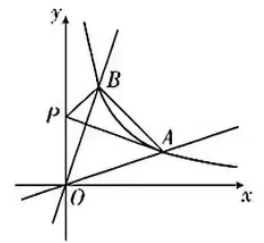
2.已知反比例函数y=k/x和一次函数y=x-1,其中一次函数的图象过（3a,b),(3a+1,b+k/3)两点．

（1)求反比例函数的关系式．

（2)如图，函数y=1/3x,y=3x的图象分别与函数y=k/x（x＞0)的图象交于A,B两点，在y轴上是否存在点P,使得ΔABP的周长最小？若存在，求出周长的最小值；若不存在，请说明理由。

数学陈老师:

【题型探究3 】反比例函数与三角形面积

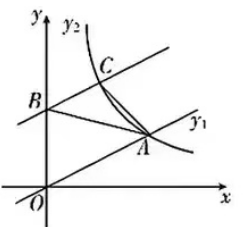
3.如图，正比例函数y₁=1/2x和反比例函数y₂=k/x（x>0)的图象交于点A(m,2).（1)求反比例函数的解析式．

（2)将直线OA向上平移3个单位后，与y轴交于点B,与y₂=k/x（x＞0)的图象交于点C,连接AB,AC,求ΔABC的面积。    

【题型探究4】 反比例函数与等腰三角形

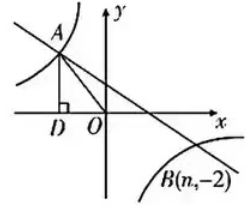
4.如图所示，在平面直角坐标系中，一次函数y=kx+b（k≠0)与反比例函数y=m/x(m≠0)的图象交于第二、四象限的A,B两点，过点A作AD⊥x轴于点D,AD=4,sin∠AOD=4/5，且点B的坐标为（n,-2).

（1)求一次函数与反比例函数的解析式．

（2)E是y轴上一点，且ΔAOE是等腰三角形，请直接写出所有符合条件的E点的坐标。

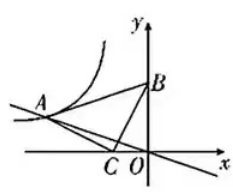
【题型探究5】 反比例函数与直角三角形

5.如图，在RtΔABC中，∠ACB=90°,AC=BC,点C(-2, 0),点B(0, 4),反比例函数y=k/x（x＜0)的图象经过点A.    

（1)求反比例函数的解析式．

（2)设直线OA的解析式为y=k₁x.

    ①直接写出不等式k/x＜k₁x的解集；

    ②将直线OA向上平移m个单位后经过反比例函数y=k/x（x＜0)的图象上的点（－1,n),求m,n的值．

数学陈老师:

【题型探究6】 反比例函数与相似三角形

6.已知RtΔABC在平面直角坐标系中的位置如图所示，A(-4, 0),线段AC交y轴于点D(0, 2),且D是AC的中点，反比例函数y=k/x（x＞0)的图象经过线段BC的中点E.    

（1)求反比例函数的解析式．

（2)如图2,G是x轴上一点，连接CG,交反比例函数y＝k/x（x＞0)的图象于点F,连接DF,交BC于点P.若CG=3FG,求ΔCDF的面积。

（3)M是直线BC右侧反比例函数图象上一点，连接EM,过点M作MN⊥EM,交x轴于点N,连接EN,当ΔEMN与ΔABC相似时，求点M的坐标。

数学陈老师:

【题型探究7】 反比例函数与平行四边形

7.如图，一次函数y=kx+b的图象与反比例函数y＝m/x的图象相交于A(-1, 4),B(a,-1)两点．    

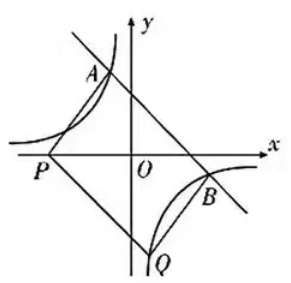
（1)求反比例函数和一次函数的表达式．

（2)点P(n,0)在x轴负半轴上，连接AP,过点B作BQ//AP,交y=m/x的图象于点Q,连接PQ. 当BQ=AP时，若四边形APQB的面积为36,求n的值．

数学陈老师:

【题型探究8】 反比例函数与矩形

8.在矩形OACB中，OB=4,OA=3,分别以OB,OA为x轴、y轴，建立如图1所示的平面直角坐标系，F是BC边上的一个动点（不与点B,C重合），过点F的反比例函数y=k/x（k＞0)的图象与边AC交于点E.    

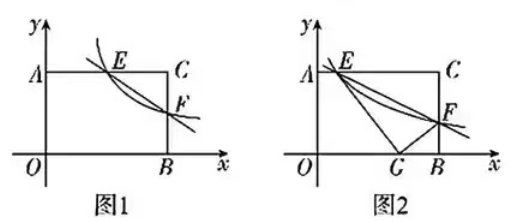
（1)当点F运动到边BC的中点时，求点E的坐标。

（2)连接EF,试探究：随着点F的运动，∠EFC的正切值是否发生变化？若不变，求出这个值；若变化，请说明理由。

（3)如图2,将ΔCEF沿EF折叠，点C恰好落在OB边上的点G处，求此时点F的坐标。

数学陈老师:

【题型探究9】反比例函数与菱形

9.如图1,菱形ABCD的边AB在平面直角坐标系中的x轴上，A(-1, 0),菱形的对角线交于点M(0, 2),过点C的反比例函数y=k/x(x＞0)与菱形的边BC交于点E.    

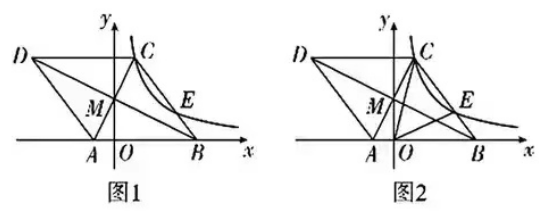
（1)求点C的坐标和反比例函数y=k/x(x＞0)表达式。

（2)如图2,连接OC,OE,求出ΔCOE的面积。

（3)P为y=k/x（x＞0)的图象上的一个动点，过点P作PH⊥x轴于点H,若点P使得ΔAOM和ΔBPH相似，请直接写出点P的横坐标。

数学陈老师:

【题型探究10】反比例函数与正方形

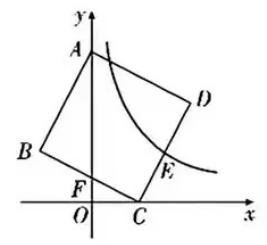
10. 如图，正方形的顶点A,C分别在y轴和x轴上，边BC的中点F在y轴上，若反比例函数y=12/x的图象恰好经过CD的中点E,则OA的长为          .    

【题型探究11】反比例函数与圆

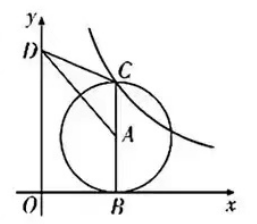
11.如图，在直角坐标系中，⊙A与x轴相切于点B,CB为⊙A的直径，点C在函数y=k/x（k＞0,x＞0)的图象上，D为y轴上一点，ΔACD的面积为6,则k的值为           .

点赞+关注

天天学习不迷路

赞赏后请留言    

可提供答案解析

空白电子文档