获取打印版及试卷详解答案见文末
2023年初中学业水平考试试卷
数学
注意事项:
1.本试卷共6页,满分120分.考试时间为120分钟.
2.答题前,考生务必先将自己的考生号、姓名、座位号等信息填写在试卷和答题卡的指定位置.请认真核对条形码上的相关信息后,将条形码粘贴在答题卡的指定位置.
3.答题时,将答案写在答题卡上.写在本试卷上无效.
4.考试结束后,将本试卷和答题卡一并交回.
一、选择题:本大题共有10小题,每小题3分,共30分.每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑.
1. 下列各式计算结果为的是( )
A. B. C. D.
2. 关于的一元一次不等式的解集在数轴上的表示如图所示,则的值为( )

A. 3 B. 2 C. 1 D. 0
3. 定义新运算“”,规定:,则的运算结果为( )
A. B. C.5 D.3
4. 如图,直线,直线与直线分别相交于点,点在直线上,且.若,则的度数为( )
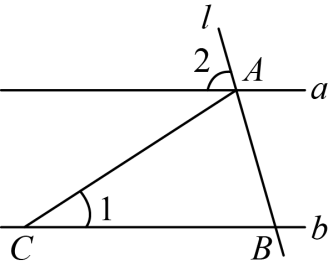
A. B. C. D.
5.几个大小相同的小正方体搭成几何体的俯视图如图所示,图中小正方形中数字表示对应位置小正方体的个数,该几何体的主视图是( )
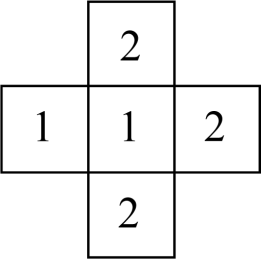
A.  B.
B. 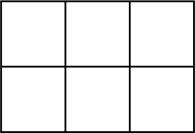 C.
C. 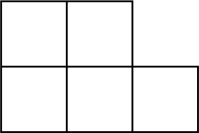 D.
D. 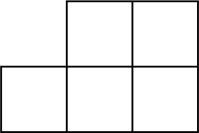
6.从1,2,3这三个数中随机抽取两个不同的数,分别记作和.若点的坐标记作,则点在双曲线上的概率是( )
A. B. C. D.
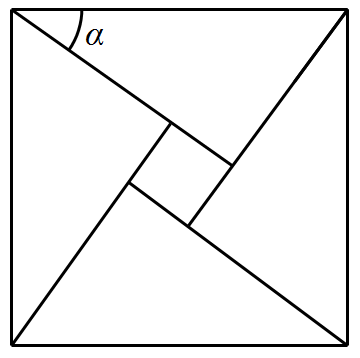
7.如图是源于我国汉代数学家赵爽的弦图,它是由四个全等直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
8.在平面直角坐标系中,将正比例函数的图象向右平移3个单位长度得到一次函数的图象,则该一次函数的解析式为( )
A. B.
C. D.
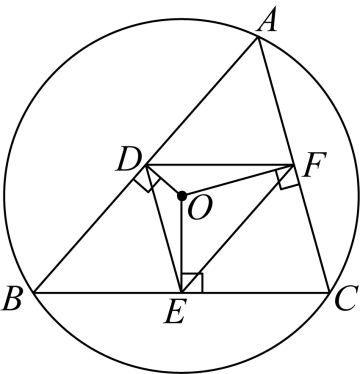
9. 如图,是锐角三角形的外接圆,,垂足分别为,连接.若的周长为21,则的长为( )
A. 8 B. 4 C. 3.5 D. 3
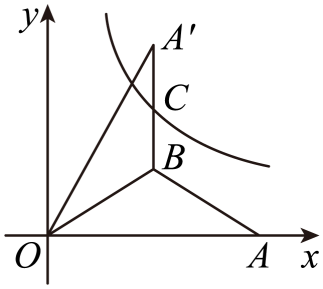
10.如图,在平面直角坐标系中,三个顶点的坐标分别为与关于直线对称,反比例函数的图象与交于点.若,则的值为( )
A. B. C. D.
二、填空题:本大题共有6小题,每小题3分,共18分.请将答案填在答题卡上对应的横线上.
11. 若为两个连续整数,且,则________.
12. 若是一元二次方程的两个实数根,则________.
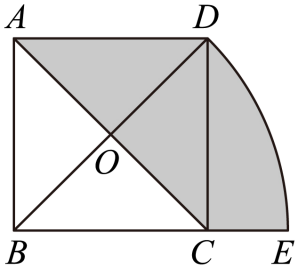
13.如图,正方形的边长为2,对角线相交于点,以点为圆心,对角线的长为半径画弧,交的延长线于点,则图中阴影部分的面积为________.
14. 已知二次函数,若点在该函数的图象上,且,则的值为________.
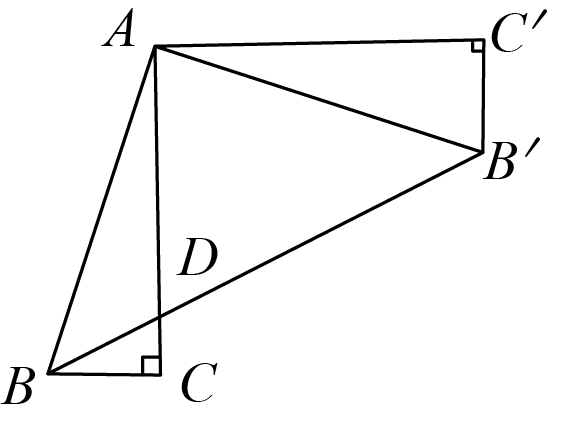
15.如图,在中,,将绕点A逆时针方向旋转,得到.连接,交于点D,则的值为________.
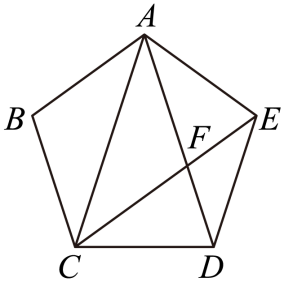
16. 如图,是正五边形的对角线,与相交于点.下列结论:
①平分; ②; ③四边形是菱形; ④
其中正确的结论是________.(填写所有正确结论的序号)
三、解答题:本大题共有7小题,共72分.请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置.
17. (1)先化简,再求值:,其中.
(2)解方程:.
18.在推进碳达峰、碳中和进程中,我国新能源汽车产销两旺,连续8年保持全球第一.图为我国某自主品牌车企2022年下半年新能源汽车的月销量统计图.
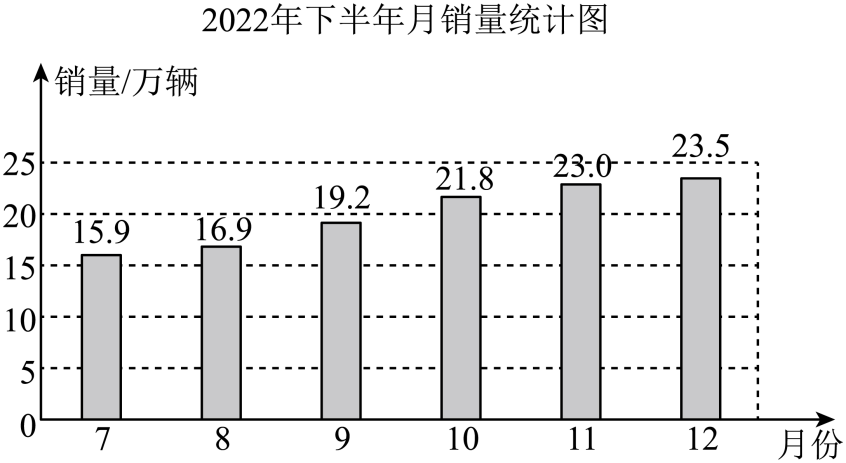
请根据所给信息,解答下列问题:
(1)通过计算判断该车企2022年下半年的月均销量是否超过20万辆;
(2)通过分析数据说明该车企2022年下半年月销量的特点(写出一条即可),并提出一条增加月销量的合理化建议.
19.为了增强学生体质、锤炼学生意志,某校组织一次定向越野拉练活动.如图,A点为出发点,途中设置两个检查点,分别为点和点,行进路线为.点在点南偏东方向处,点在A点的北偏东方向,行进路线和所在直线的夹角为.
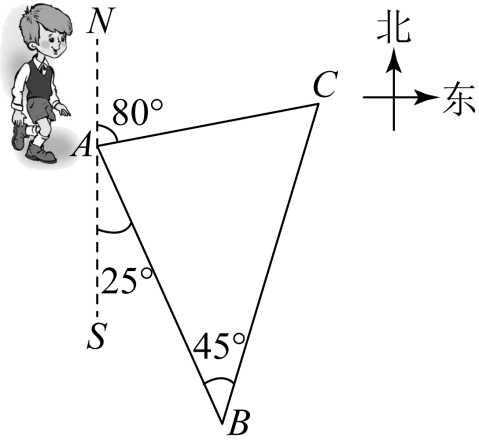
(1)求行进路线和所在直线的夹角的度数;
(2)求检查点和之间的距离(结果保留根号).
20.随着科技发展,扫地机器人已广泛应用于生活中,某公司推出一款新型扫地机器人,经统计该产品2022年每个月的销售情况发现,每台的销售价格随销售月份的变化而变化、设该产品2022年第(为整数)个月每台的销售价格为(单位:元),与的函数关系如图所示(图中为一折线).
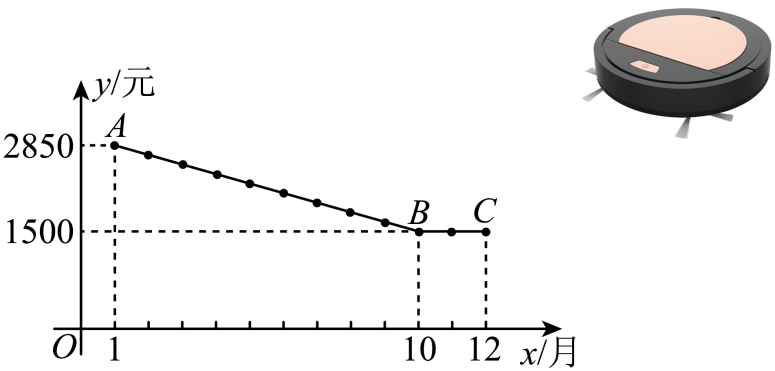
(1)当时,求每台的销售价格与之间的函数关系式;
(2)设该产品2022年第个月的销售数量为(单位:万台),m与的关系可以用来描述,求哪个月的销售收入最多,最多为多少万元?(销售收入每台的销售价格销售数量)
21. 如图,是的直径,是弦,是上一点,是延长线上一点,连接.
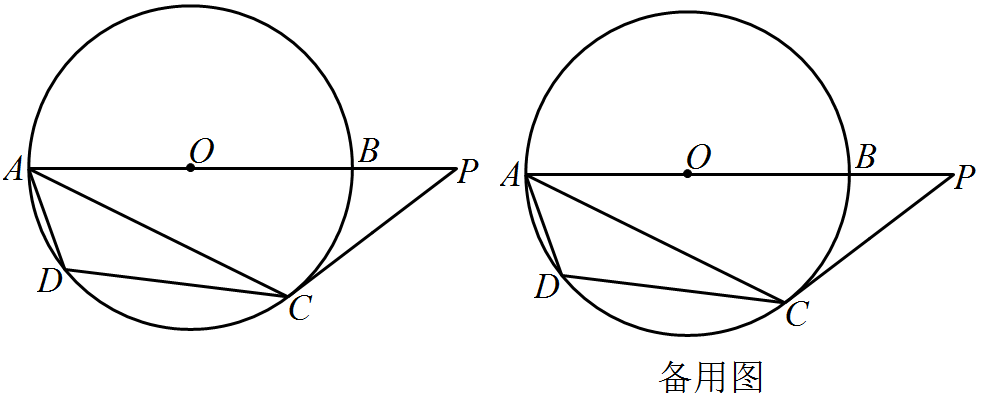
(1)求证:;(请用两种证法解答)
(2)若,半径为3,,求的长.
22.如图,在菱形中,对角线相交于点,点分别是边,线段上的点,连接与相交于点.
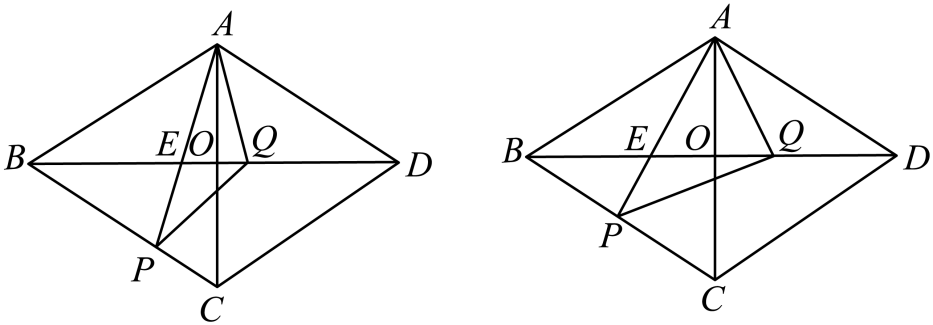
(1)如图1,连接.当时,试判断点是否在线段垂直平分线上,并说明理由;
(2)如图2,若,且,
①求证:;
②当时,设,求的长(用含的代数式表示).
23.如图,在平面直角坐标系中,抛物线交轴于点,直线交抛物线于两点(点在点的左侧),交轴于点,交轴于点.
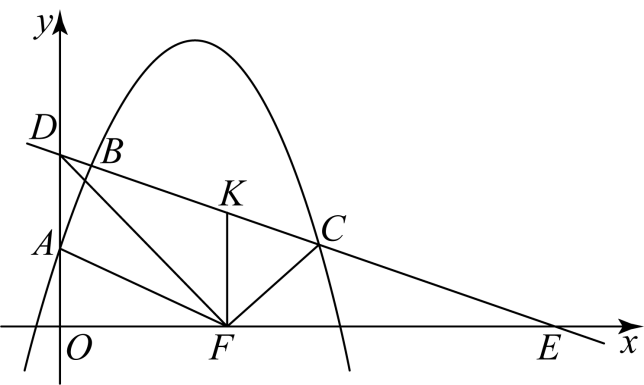
(1)求点的坐标;
(2)线段上一点,连接,且.
①求证:是直角三角形;
②的平分线交线段于点是直线上方抛物线上一动点,当时,求点的坐标.
下载
关注本公众号
并在对话界面回复
“231908”
自动获取试题和答案下载链接
分享是一种美德,点赞是一种支持 分享“朋友圈”、点亮 “在看”可以获取多套真题 2023年全国数学中考真题试卷免费送
扫一扫上面二维码加“爱都数理化”微信,获取更多真题 获取多套真题只能通过微信或QQ发送 |
-aidu2021-
资料来源于互联网
如有侵权,请及时告知,我将立即删除
整编:东方龙
爱都,不是名师的聚集地
爱都,只是知识的搬运工
渴望超越,从爱都出发
可以点“在看”给我一朵  吗?
吗?







