中考数学冲刺复习选择题难点突破(模块二)
中考数学冲刺复习
选择题难点突破
图形变换与二次函数中的多结论问题
一、知识技能梳理
【模块一】图形变换-轴对称
图形的轴对称是初中三大图形变换中的一种,在中考中常常会以折叠的形式出现。折叠的载体有各种各样的图形,考查的问题有求线段长度(或线段最值、线段比值)、角度、图形周长、面积、三角函数等等。虽然有纷繁复杂的情形,但解决问题的突破口始终是轴对称的性质和背景图形的性质。
【轴对称的性质】
1、全等性:全等图形、对应边相等、对应角相等。
2、对称性:对应点所连线段被对称轴垂直平分。
【解题步骤】
1、明确轴对称性质(全等性、对称性),关注背景图性质和已知条件。
2、结合背景图性质、轴对称性质和已知条件,找条件之间的联系,进行等量转化。
3、利用基本方法:构造方程(勾股定理、全等三角形、相似三角形、等面积),进行求解,进而解决问题。
【模块二】图形变换-旋转
图形的旋转是初中三大图形变换中的一种,在中考中常常以综合题的形式出现。图形的旋转常见的类型有两种,一种是题目已有明显的较为完整的共顶点的旋转图形,这类型的题目难度不大。第二种类型是题目没有明显旋转图形,需要根据题目中的条件构造旋转模型,使问题巧妙解决。本模块重点学习第二种类型。若题目中出现共顶点等线段,如等腰直角三角形或等边三角形,则可以作辅助线构造旋型全等三角形;若题目中无共顶点等线段,但有共点等角,则可以做辅助线构造旋转相似三角形。构造旋转图形的共同特点是寻找全等三角形或相似三角形,利用它们的性质解题,此类旋转问题,有时也会结合动点问题求最值。
【模块三】二次函数中的多结论问题
二次函数中的多结论问题通常是选择题常考的压轴题。
【考点如下】
1. abc<0,考a,b,c符号
2. a±b+c=0,a-2b+4c=0, 4a+c<2b,(a+c)2<b2,考特殊点
3. 2a-b=0,考对称轴
4. 3a+c>0, 3b+2c<0, 1≤a≤3/4,考对称轴与特殊点结合
5. m(am+b)+b<ac ,考最值(顶点)
6. b2+2a>4ac,考最值(顶点纵坐标)
7. 4ac-b2<0,考图象与x轴交点个数
8. (-4,y1),(1,y2)在抛物线上,则y1<y2 ,考增减性和对称性
9. 方程ax2+bx+c+2=0有两个不相等的实数根,考函数与方程的关系,平移
二、学习过程
模块二:图形变换-旋转
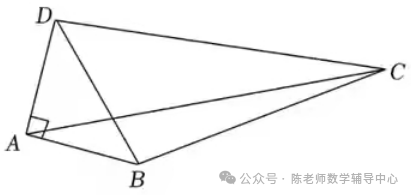
例1.如图,四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=30°,BC=2,AC=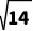 ,则CD的长为()
,则CD的长为()
A. 4 B. 2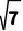 C. 5 D.
C. 5 D. 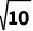
【小结】
1、共顶点等线段可以构造旋转型全等三角形解决问题。
2、三角形中,已知两边和一个特殊角,求第三边:可通过作垂线构造特殊直角三角形解决问题。
例2.如图,在矩形ABCD中,AB=3,BC=4,P是对角线AC上的动点,连接DP,将直线DP绕点P顺时针旋转使∠DPG=∠DAC,且过D作DG⊥PG,连接CG,则CG最小值为( )。
A. 36/25 B.27/25 C.48/25 D.3/2
方法一:转化CG边。
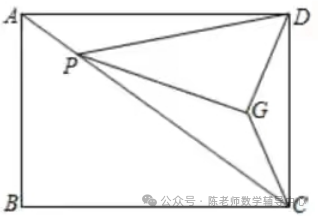
方法二:寻找G点运动轨迹。
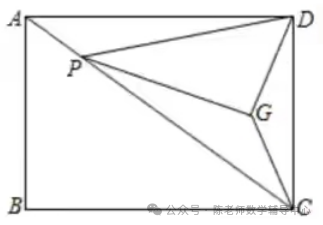
【小结】未知运动轨迹的动点线段求最值问题:
1、通过相似或全等转化为已知运动轨迹的动点线段的最值问题,一般是构造旋转图形。
2、求出该动点的轨迹,结合图象进行分析。
数学陈老师:
练 习 2
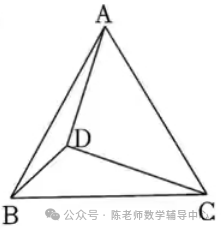
1.若点D为等边ΔABC内一点,且DA=4,DB=3,DC=5,则此等边三角形ABC的面积为()
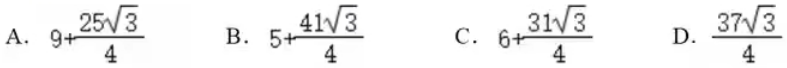
2.如图所示,在RtΔABC中,∠C=90°,AB=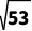 ,tanB=7/2,将ΔABC绕点C顺时针旋转至ΔA'B'C的位置,且点B'在AB上,A'B'交AC于点D,则ΔA'DC的面积为()
,tanB=7/2,将ΔABC绕点C顺时针旋转至ΔA'B'C的位置,且点B'在AB上,A'B'交AC于点D,则ΔA'DC的面积为()
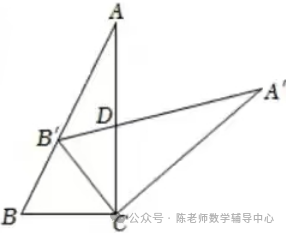

3.如图,将矩形ABCD绕点A按逆时针方向旋转一定角度后,BC的对应边B'C交CD边于点G,如果当AB'=B'G时量得AD=7,CG=4,连接BB'、CC',那么CC'/BB'的值为()

4.如图,ΔABC是等边三角形,AB=4,E是AC的中点,D是直线BC上一动点,
线段ED绕点E逆时针旋转90°,得到线段EF,当点D运动时,则AF的最小值为()
A. 2 B. 2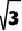 C.
C. 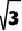 D.
D. 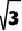 +1
+1
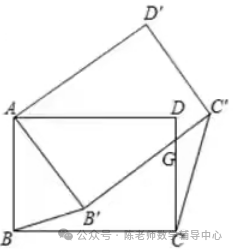
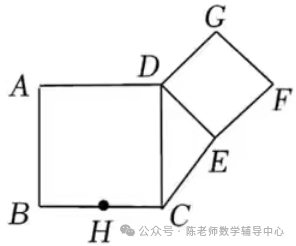
5.如图,在正方形ABCD中,AB=6,点H为BC中点,点E绕着点C旋转,且CE=4,在DC的右侧作正方形DEFG,则线段FH的最小值是()
A. 9-4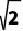 B. 8-4
B. 8-4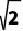 C. 9-6
C. 9-6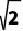 D. 10-6
D. 10-6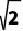
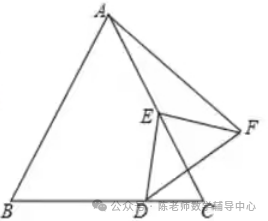
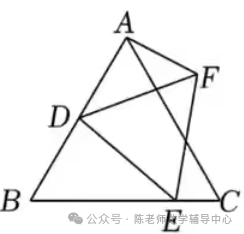
6.如图,等边三角形ABC的边长为4,点D是AB边的中点,点E是BC边上的
一个动点,以DE为边作等边三角形DEF,连接AF,则AF的最小值为()
A. 2 B. 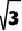 C. 2
C. 2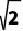 D. 2
D. 2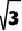
点赞+关注
天天学习不迷路
赞赏后请留言
可提供答案解析
空白电子文档





