中考数学冲刺复习动点压轴题常考题型考前强化训练

中考数学冲刺复习动点压轴题常考题型考前强化训练

中考数学冲刺复习

动点压轴题常考题型

考前强化训练

  动点是最近几年中考数学压轴常考题型，难度很大，不容易得分，往往中等与优秀学生就靠这一类题拉分，因此掌握动点题型就意味着得高分。

【动点类选择题精练】

1.如图1,在菱形ABCD中，∠A=60°,动点P从点A出发，沿折线AD→DC→CB方向匀速运动，运动到点B停止。设点P的运动路程为x,ΔAPB的面积为y,y与x的函数图象如图2所示，则AB的长为（）

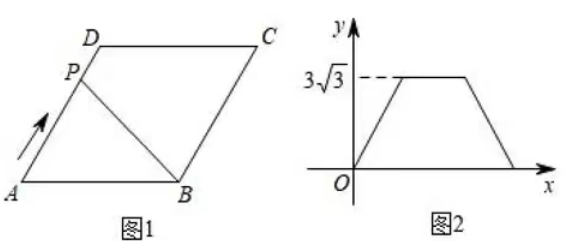
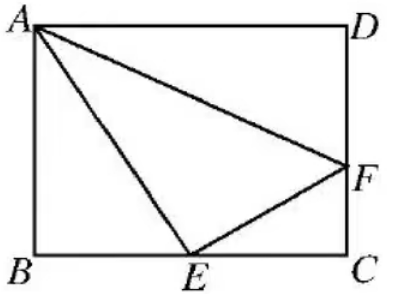
A.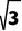

B. 2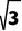

C. 3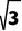

D. 4

2.如图，在矩形ABCD中，BC=1,∠ADB=60°,动点P沿折线AD→DB运动到点B,同时动点Q沿折线DB→BC运动到点C,点P,Q在矩形边上的运动速度为每秒1个单位长度，点P,Q在矩形对角线上的运动速度为每秒2个单位长度．设运动时间为t秒，ΔPBQ的面积为S,则下列图象能大致反映S与t之间函数关系的是（）

3.如图，在矩形ABCD中，AB=6,BC=8,点E是BC中点，点F是边CD上的任意一点，当ΔAEF的周长最小时，则DF的长为（）

  A. 1    

  B. 2

  C. 3

  D. 4

数学陈老师:

4.如图，等腰ΔABC的面积为2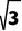,AB=AC,BC=2.作AE//BC且AE=1/2BC. 点P是线段AB上一动点，连接PE,过点E作PE的垂线交BC的延长线于点F,M是线段EF的中点。那么，当点P从A点运动到B点时，点M的运动路径长为（）

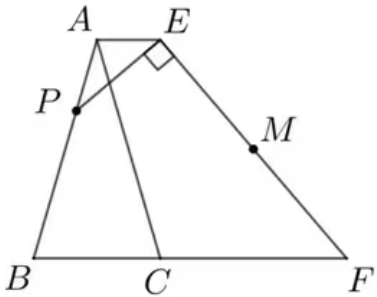
A.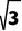

B. 3

C. 2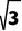

D. 4

5.如图①,在矩形ABCD中，H为CD边上的一点，点M从点A出发沿折线AH-HC-CB运动到点B停止，点N从点A出发沿AB运动到点B停止，它们的运动速度都是1cm/s,若点M、N同时开始运动，设运动时间为t(s),ΔAMN的面积为S(c㎡),已知S与t之间函数图象如图②所示，则下列结论正确的是（）    

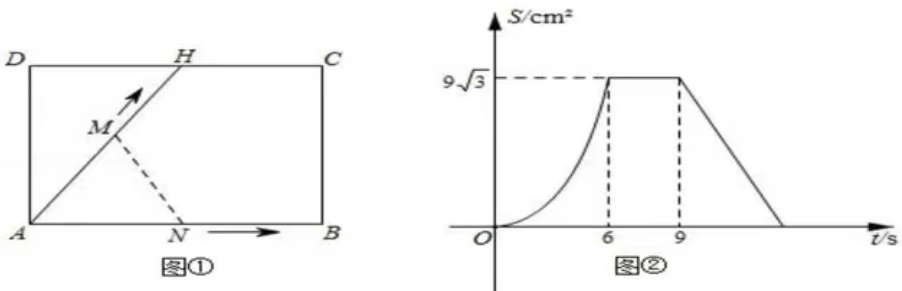
①当0＜t≤6时，ΔAMN是等边三角形．

②在运动过程中，使得ΔADM为等腰三角形的点M一共有3个．

③当0＜t≤6时，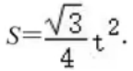

④当t=9+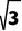时，ΔADH∽ΔABM.

⑤当9＜t＜9+3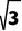时，S=-3t+9+3.

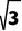  A. ①③④

  B. ①③⑤

  C. ①②④

  D. ③④⑤

数学陈老师:

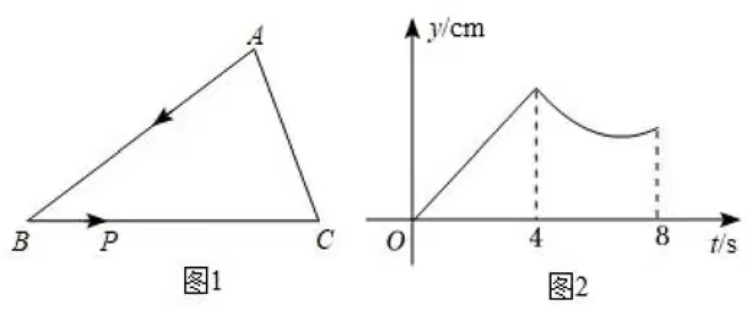
6.图（1),在RtΔABC中，∠A=90°,点P从点A出发，沿三角形的边以1cm/秒的速度逆时针运动一周，图（2)是点P运动时，线段AP的长度y(cm)随运动时间x(秒）变化的关系图象，则图（2)中P点的坐标是（）    

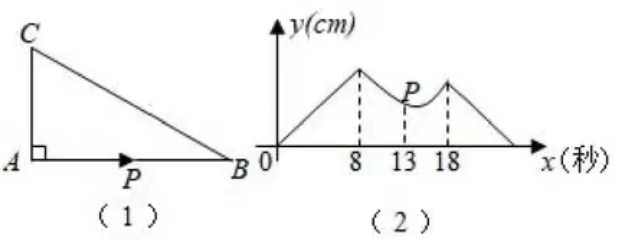
A. (13,4.5)

B. (13,4.8)

C. (13,5)

D. (13,5.5)

7.如图1,在ΔABC中，AB=BC,BD⊥AC于点D(AD＞BD).动点M从A点出发，沿折线AB→BC方向运动，运动到点C停止。设点M的运动路程为x,ΔAMD的面积为y,y与x的函数图象如图2,则AC的长为（）

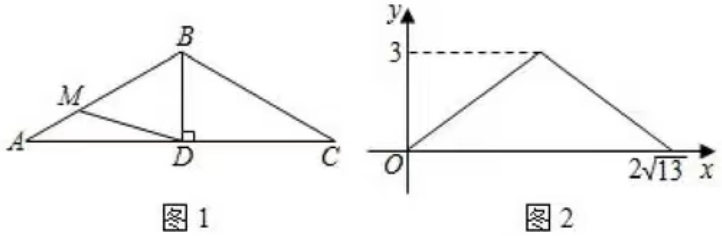
A. 3

B. 6

C. 8    

D. 9

8.如图①所示（图中各角均为直角），动点P从点A出发，以每秒1个单位长度的速度沿A→B→C→D→E路线匀速运动，ΔAFP的面积y随点P运动的时间x(秒）之间的函数关系图象如图②所示，下列说法正确的是（）

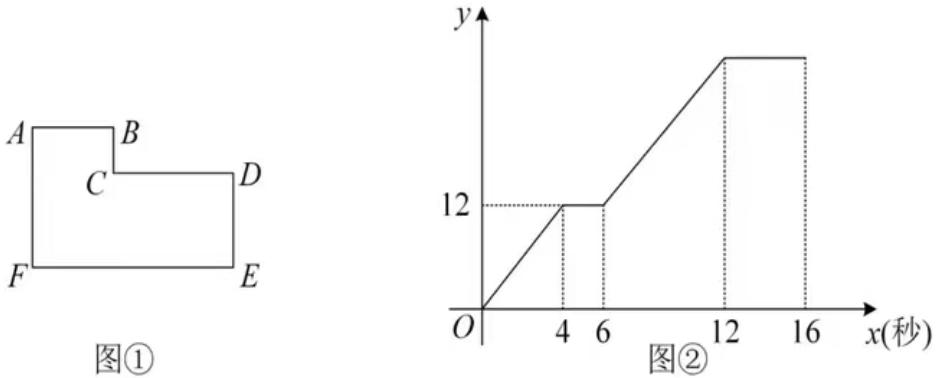
A. AF=5

B. AB=4

C. DE=3

D. EF=8

数学陈老师:

【动点类填空题精炼】

1.如图1,在ΔABC中，∠B=36°,动点P从点A出发，沿折线A→B→C匀速运动至点C停止．若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为y(cm),y与t的函数图象如图2所示．当AP恰好平分∠BAC时，t的值为    .    

2.在矩形ABCD中，AB=9,AD=12,点E在边CD上，且CE=4,点P是直线BC上的一个动点。若ΔAPE是直角三角形，则BP的长为      .

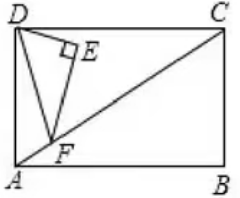
3.如图，在矩形ABCD中，AB=4,∠DCA=30°,点F是对角线AC上的一个动点，连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是       .

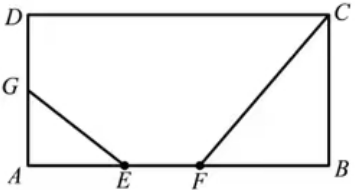
4.如图，矩形ABCD中，AB=4,BC=2,G是AD的中点，线段EF在边AB上左右滑动；若EF=1,则GE+CF的最小值为       .    

数学陈老师:

5.如图1,在四边形ABCD中，BC//AD,∠D=90°,∠A=45°,动点P,Q同时从点A出发，点P以2cm/s的速度沿AB向点B运动（运动到B点即停止），点Q以2cm/s的速度沿折线AD→DC向终点C运动，设点Q的运动时间为x(s),ΔAPQ的面积为y(c㎡),若y与x之间的函数关系的图像如图2所示，当x=7/2(s)时，则y=        c㎡.

数学陈老师:

【动点类解答题精炼】    

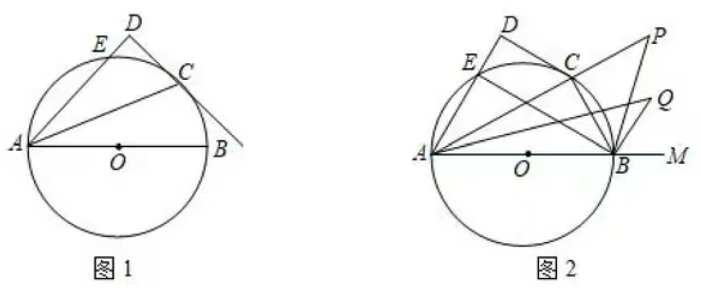
1.如图1,AB是⊙O的直径，点E是⊙O上一动点，且不与A,B两点重合，∠EAB的平分线交⊙O于点C,过点C作CD⊥AE,交AE的延长线于点D.

（1)求证：CD是⊙O的切线；

（2)求证：AC²=2AD·AO;

（3)如图2,原有条件不变，连接BE,BC,延长AB至点M,∠EBM的平分线交AC的延长线于点P, ∠CAB的平分线交∠CBM的平分线于点Q. 求证：无论点E如何运动，总有∠P= ∠Q.

数学陈老师:

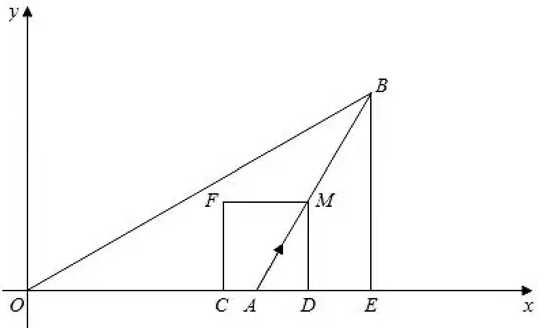
2.如图，在平面直角坐标系中，ΔAOB的边OA在x轴上，OA=AB,且线段OA的长是方程x²-4x-5=0的根，过点B作BE⊥x轴，垂足为E,tan∠BAE=4/3，动点M以每秒1个单位长度的速度，从点A出发，沿线段AB向点B运动，到达点B停止。过点M作x轴的垂线，垂足为D,以MD为边作正方形MDCF,点C在线段OA上，设正方形MDCF与ΔAOB重叠部分的面积为S,点M的运动时间为t(t＞0)秒．    

（1)求点B的坐标；

（2)求S关于t的函数关系式，并写出自变量t的取值范围；

（3)当点F落在线段OB上时，坐标平面内是否存在一点P,使以M、A、O、P为顶点的四边形是平行四边形？若存在，直接写出点P的坐标；若不存在，请说明理由。

数学陈老师:

3.如图一所示，在平面直角坐标中，抛物线y=ax²+2x+c经过点A(-1, 0)、B(3, 0),与y轴交于点C,顶点为点D. 在线段CB上方的抛物线上有一动点P,过点P作PE⊥BC于点E,作PF//AB交BC于点F.    

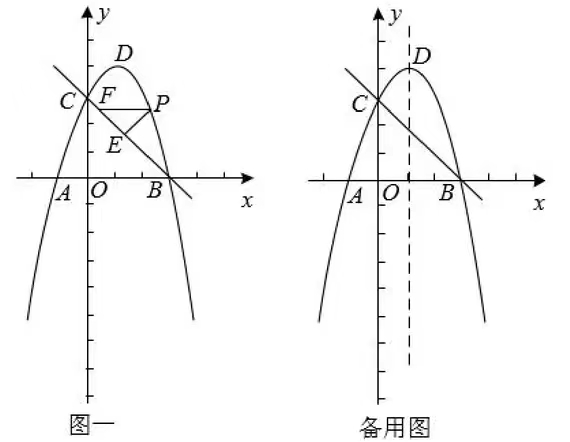
（1)求抛物线和直线BC的函数表达式；

（2)当ΔPEF的周长为最大值时，求点P的坐标和ΔPEF的周长；

（3)若点G是抛物线上的一个动点，点M是抛物线对称轴上的一个动点，是否存在以C、B、G、M为顶点的四边形为平行四边形？若存在，求出点G的坐标，若不存在，请说明理由。

点赞+关注

天天学习不迷路

赞赏后请留言

可提供答案解析    

空白电子文档