攀登中考数学高峰:特殊几何图形——直角△
四季读书网
45
命题之道,用教材里的数学语言、符号巧妙地将数学结论和数学知识点间的关联隐藏在题目的条件和问题里。
解题之法,用侦探的慧眼、思维、推理迅速地在条件与问题之间建构解题知识链,再用数学语言、符号规范地呈现命题人的数学思维和思想。
解铃无须系铃人。
典例选讲
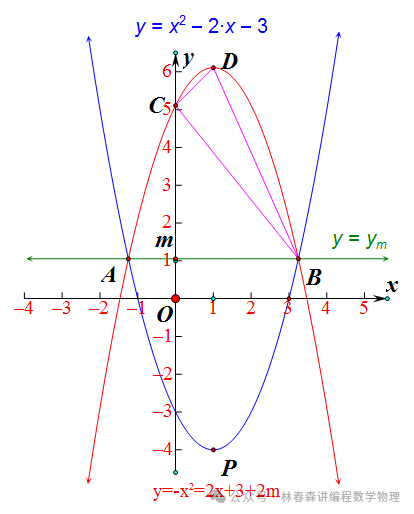
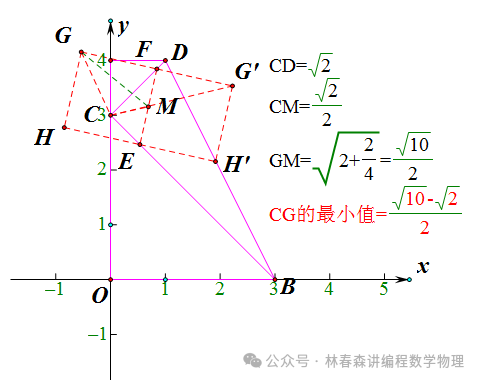
如图,在平面直角坐标系xOy中,抛物线L1:y=x^2-2x-3的顶点为P。直线l过点M(0,m)(m≥-3),且平行x轴,与抛物线L1交于A、B两点(B在A的右侧),将抛物线L1沿直线l翻折得到抛物线L2,抛物线L2交y轴于点C,顶点为D。 ⑵连接BC、CD、DB,若△BCD为直角三角形,求此时L2的函数解析式;⑶在⑵的条件下,若△BCD的面积为3,E、F两点分别在边BC、CD上运动,且EF=CD,以EF为一边作正方形EFGH,连接CG,写出CG长度的最小值,并简要说明理由。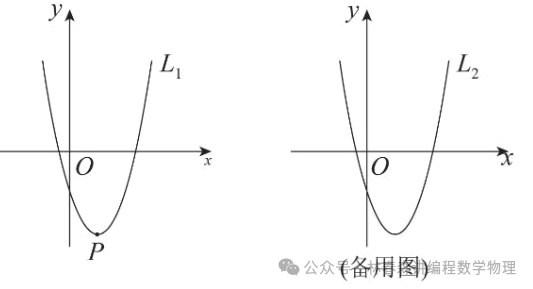
|
①抛物线L1:y=x^2-2x-3,隐藏:顶点,对称轴,图象开口朝向,与坐标轴的交点信息。②直线l过点M(0,m)(m≥-3),且平行x轴,隐藏:直线可以在x轴下方、重合或上方,直线与抛物线一定有交点。③翻折,隐藏:新的抛物线图象与原抛物线图象关于直线l对称;图象对应点坐标的中点坐标落在直线上;新抛物线图象的对称轴与原抛物线图象对称轴重合。④△BCD为直角三角形,隐藏:哪个角是直角,需要讨论;(m≥-3),会有不合题意的情形。⑤⑵的条件下,若△BCD的面积为3,隐藏:满足⑵的条件的△BCD的面积,还需要进一步验证,排除不满足△BCD的面积为3的情形。⑥EF=CD,隐藏:刚性边,中点的轨迹在一个定圆上。⑦以EF为一边作正方形EFGH,隐藏:可以向EF左侧,也可以向EF右侧作正方形。m=1,直线l:y=1,对折,求L2解析式,配方,求顶点坐标。
点坐标,两点间的距离公式,分类讨论直角的所在的顶点,勾股定理,验根。 |
|
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌抄袭侵权/违法违规的内容, 请发送邮件至23467321@qq.com举报,一经查实,本站将立刻删除;如已特别标注为本站原创文章的,转载时请以链接形式注明文章出处,谢谢!







